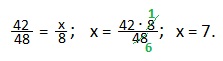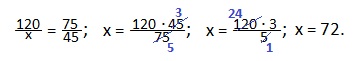Что такое обратно пропорциональные величины
Математика. 6 класс
Конспект урока
Прямая и обратная пропорциональность
Перечень рассматриваемых вопросов:
Равенство двух отношений называют пропорцией.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Теоретический материал для самостоятельного изучения
Пусть ручка стоит пять рублей, составим таблицу для нахождения стоимости от одной до семи ручек.
Из таблицы видно, что пять ручек стоят в пять раз больше, чем одна ручка. Говорят, что стоимость покупки прямо пропорциональна количеству купленных ручек.
Стоимость покупки прямо пропорциональна количеству купленных ручек.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Цена двух ручек 10 руб. Сколько нужно заплатить за пятнадцать таких же ручек?
Стоимость покупки прямо пропорциональна количеству ручек.
Запишем кратко условие задачи:
Чтобы найти неизвестный средний член пропорции, нужно произведение её крайних членов разделить на известный средний член пропорции:
Ответ: 15 ручек стоят 75 рублей.
На 600 рублей хотят купить несколько одинаковых коробок конфет. Зависимость количества купленных коробок конфет от цены одной коробки задана в таблице:
С увеличением цены за одну коробку в несколько раз количество коробок конфет, которые можно купить, уменьшается во столько же раз.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Грузовая машина, двигаясь со скоростью 60 километров в час, доезжает от одного города до другого за 3 часа. За сколько часов это же расстояние преодолеет легковой автомобиль, если его скорость 90 километров в час?
При постоянном пути скорость и время движения обратно пропорциональны.
Запишем кратко условие задачи:
Ответ: легковой автомобиль преодолеет расстояние между городами за 2 часа.
Свойство прямо пропорциональных величин.
Отношение прямо пропорциональных величин всегда остаётся неизменным.
Величину этого отношения называют коэффициентом прямой пропорциональности.
5 – коэффициент прямой пропорциональности.
Свойство обратно пропорциональных величин: произведение обратно пропорциональных величин всегда остаётся неизменным.
100 руб. · 6 коробок = 200 руб. · 3 коробки = 600 руб. · 1 коробку = 600
60 км/ч · 3 ч = 90 · 2 ч = 180
Между двумя городами расстояние равно 32 км. На карте отрезок между ними равен 2 см. Найдите масштаб карты.
Расстояние на местности и отрезок на карте – прямо пропорциональная зависимость.
Обозначим х см на местности отрезок в 1 см на карте.
Разбор заданий тренировочного модуля
Для решения задачи нужно понять какая происходит зависимость между величинами. Зависимость между массой и объёмом прямо пропорциональная. Составим пропорцию и найдём её неизвестный член.
№ 2. Ввод с клавиатуры пропущенных элементов в текст.
Зависимость между расходом угля и периодом, на который этого угля хватит, – обратно пропорциональная. То есть чем больше мы сжигаем угля в день, тем на меньшее количество дней нам этого угля хватит.
Прямая и обратная пропорциональность
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
a и d называются крайними членами, b и c — средними.
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
Формула обратной пропорциональности
где y и x — это переменные величины,
k — постоянная величина, которую называют коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Соотношения равны, но перевернуты относительно друг друга.
6.1.5. Обратно пропорциональные величины
I. Обратно пропорциональные величины.
Пусть величина у зависит от величины х. Если при увеличении х в несколько раз величина у уменьшается во столько же раз, то такие величины х и у называются обратно пропорциональными.
Примеры.
1. Скорость и время при одинаковой длине пути. Если от А до В 200 км, то при скорости 50 км/ч понадобится 4 часа, а при скорости 40 км/ч понадобится 5 часов, т.е. если скорость уменьшается, то время увеличивается, а если скорость увеличивается, то время уменьшается. Это изобразится так:
2. Количество рабочих и время при определенном объеме работ. Если шести рабочим нужно на выполнение определенной работы 4 часа, то трем рабочим на выполнение той же работы потребуется 8 часов, т.е. чем меньше работников, тем больше нужно времени, чтобы выполнить определенную работу.

3) Длина и ширина прямоугольника при постоянной площади прямоугольника. Если площадь участка прямоугольной формы с длиной 8 м, равна 48 м², то его ширина будет равна (48:8=6)м. Если же длину взять больше в 2 раза (16 м), то ширина уменьшится тоже в 2 раза (48:16=3)м.
II. Свойство обратной пропорциональности величин.
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Задача 1. Изготавливая по 42 детали в час, рабочий трудился 8 часов. Сколько времени ему понадобилось бы на эту же работу, если бы он делал в час по 48 деталей?
Решение. Составим схему по условию задачи:
Имеем обратно пропорциональную зависимость: во сколько раз больше деталей в час рабочий будет изготавливать, во столько же раз меньше ему потребуется времени на одну и ту же работу. Используя свойство обратной пропорциональности, запишем:
Ответ: рабочий выполнит ту же работу за 7 часов.
Задача 2. Бассейн можно наполнять через одну из двух труб.Через первую трубу, со скоростью 2 литра в 1 секунду, бассейн наполняется за 45 минут. Какова скорость наполнения бассейна через вторую трубу, если весь бассейн наполняется через вторую трубу за 1 час 15 минут.
Решение.
По условию задачи через первую трубу в бассейн вытекает 2 литра за 1 секунду или 2·60=120 литров за 1 минуту (1 минута=60 секунд), и бассейн наполняется за 45 минут.
Через вторую трубу бассейн наполняется за 1 час 15 минут. Времени требуется больше, значит, скорость наполнения меньше. Имеем обратно пропорциональные величины: скорость наполнения и время наполнения бассейна. Обозначим скорость наполнения бассейна через вторую трубу через х.
Во сколько раз скорость наполнения меньше, во столько раз больше потребуется времени для заполнения бассейна.
Мы нашли скорость наполнения бассейна через вторую трубу в литрах в минуту. Итак, через вторую трубу бассейн наполняется со скоростью 72 литра в минуту или 72:60=1,2 литров в секунду.
Ответ: через вторую трубу в бассейн вливается 1,2 литра в 1 секунду.
Урок 23 Бесплатно Прямая и обратная пропорциональные зависимости
На этом уроке мы рассмотрим, что такое прямая и обратная пропорциональные зависимости, научимся оформлять и решать задачи с помощью пропорции, устанавливая пропорциональную зависимость между величинами в ней, рассмотрим примеры задач на прямую и обратную пропорциональную зависимость.
Прямая и обратная пропорциональность
Давайте сначала разберемся, что такое пропорциональность.
Зависимость величин друг от друга может быть прямой и обратной.
Отношение между величинами описываются прямой или обратной пропорциональностью.
Прямая пропорциональность выражается так: \(\mathbf
Обратная пропорциональность выражается так: \(\mathbf
x и y величины, зависящие друг от друга.
Пример
Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.
По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.
Какова эта зависимость, сейчас и рассмотрим.
Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.
Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.
Пусть одна клетка равна 1 см. Рассмотрим рисунок:
Ширина прямоугольника b постоянная величина
b = 4 см
a1 = 6 см
a2 = 7 см
Найдем площади прямоугольников S1 и S2
\(\mathbf
\(\mathbf
Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.
Рассмотрим другой вариант зависимости
Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см
Площадь прямоугольника S постоянная величина
S = 24 см 2
b1 = 4 см
Увеличим высоту прямоугольника- сторону прямоугольника b1 на 2 см, получим
b2 = 6 см
Найдем ширину прямоугольника- сторону a2
Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.
Таким образом, мы подошли к основным понятиям пропорциональной зависимости. Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:
1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.
2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.
Примеров прямой и обратной пропорциональности множество.
Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.
Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.
Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается
Пройти тест и получить оценку можно после входа или регистрации
Алгоритм решение задач с прямой и обратной пропорциональной зависимостью
Алгоритм решения задач на пропорциональную зависимость состоит из нескольких основных пунктов:
— Стрелки, которые направлены в одну сторону, обозначают прямую пропорциональную зависимость величин
— Стрелки, которые направлены в разные стороны, обозначают обратную пропорциональную зависимость величин.
5. Записать пропорцию, учитывая характер пропорциональности величин
6. Составить уравнение
7. Найти неизвестный член уравнения (искомую величину)
8. Записать ответ задачи
Важно помнить, что при составлении краткой записи задачи величины с одинаковыми единицами измерения записывают друг под другом.
Если между величинами прямая пропорциональная зависимость, то пропорция составляется точно в соответствии с краткой записью задачи.
Если между величинами обратная пропорциональная зависимость, то при составлении пропорции одноименные величины меняются местами в одном любом из столбцов таблицы (логической схемы) краткой записи задачи.
Другими словами, при прямо пропорциональной зависимости отношение значений одной величины равно отношению соответствующих значений другой величины.
При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.
Пройти тест и получить оценку можно после входа или регистрации
Прямая и обратная пропорциональность
Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.
Пропорциональность величин может быть прямой и обратной.
Прямая пропорциональность
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Рассмотрим пример прямой пропорциональности на формуле пути:
где s — это путь, v — скорость, а t — время.
При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
| Скорость v = 5 км/ч | |||||
|---|---|---|---|---|---|
| Время t (ч) | 1 | 2 | 4 | 8 | 16 |
| Путь s (км) | 5 | 10 | 20 | 40 | 80 |
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
| 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5. |
| 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
| Время t = 2 ч | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 5 | 15 | 45 | 90 |
| Расстояние s (км) | 10 | 30 | 90 | 180 |
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
| 10 | = | 30 | = | 90 | = | 180 | = 2. |
| 5 | 15 | 45 | 90 |
Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
Формула прямой пропорциональности
Формула прямой пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Формула обратной пропорциональности
Формула обратной пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности: