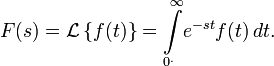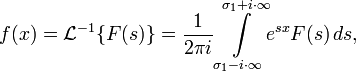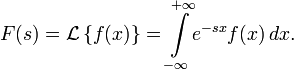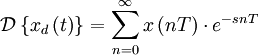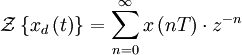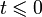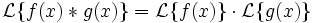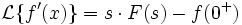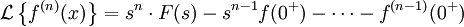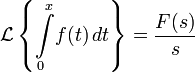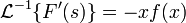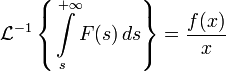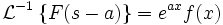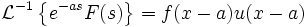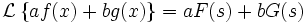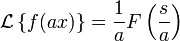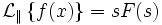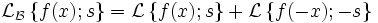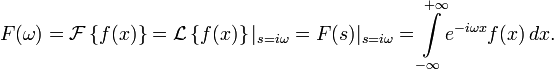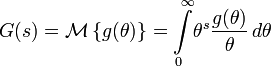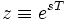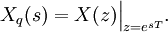Что такое обратное преобразование

Использование обратного преобразования Лапласа для анализа динамических звеньев систем управления

До настоящего времени в арсенале средств высокоуровневого языка программирования Python отсутствовали модули для численного преобразования передаточных функций элементов САУ из частотной области во временную.

Поскольку функции обратного преобразования Лапласа широко используются при анализе динамических систем контроля измерения и управления, использование Python для указанных целей было весьма затруднительно, поскольку приходилось использовать менее точное обратное Фурье преобразование [1].

Указанную проблему решает модуль mpmath библиотеки Python свободного распространения (под лицензией BSD), предназначенный для решения задач вещественной и комплексной арифметики с плавающей точкой и заданной точностью.

Работу над модулем ещё в 2007 году начал Fredrik Johansson [2], и, благодаря помощи многих участников проекта, в настоящее время mpmath приобрёл возможности серьёзного математического пакета.

Однако нас будет интересовать только заявленная в статье тема, реализуемая при помощи одношагового алгоритма invertlaplace. В качестве примера рассмотрим сравнение результатов обратного преобразования Лапласа передаточной функции w(p)=1/(1+p)** 2 при помощи invertlaplace с известной переходной функцией h(t)=e**-t от указанной передаточной функции:

Тестовый пример ограничен по объёму, но и на нём видно, что одношаговый алгоритм invertlaplace имеет высокую точность и не критичное время выполнения для ограниченного числа значений времени.

В рассмотренном примере был использован метод talbot, об особенностях других методов можно прочесть в документации [3].

Однако следует учитывать, что все численные методы обратного преобразования Лапласа требуют, чтобы их абсцисса сдвигалась ближе к началу координат для больших времен. Если абсцисса сдвинется влево от самой правой координаты в области Лапласа, ответ будет совершенно неверным.

Поэтому необходимо провести исследование применимости численного обратного преобразования Лапласа для определённых передаточных функций и оценить погрешность в сравнении с другим методом, в данной публикации это метод обратного преобразования Фурье.

1. Построение переходной характеристики объекта управления по его передаточной функции с использованием invertlaplace

Допустим, у нас есть водно-водяной теплообменник с передаточной функцией по каналу, температура нагреваемой воды – расход греющей воды.Преобразование Лапласа выходного сигнала — передаточная функция объекта управления умноженная на 1/p (единичного возмущения по расходу греющей воды) с учётом запаздывания τ имеет следующий вид:

где: Ti – постоянные времени звеньев; K – статический коэффициент передачи; p ¬ оператор Лапласа.

Получим переходную характеристику объекта с запаздыванием и самовыравниванием:

2. Построение переходной характеристики ПИД- регулятора по его передаточной функции с использованием invertlaplace

Изображение по Лапласу передаточной функции ПИД регулятора имеет вид:

где: Td, Ti – постоянные времени, дифференцирующего и интегрирующего звеньев; Kp, Kd – статические коэффициенты передачи пропорционального и дифференцирующего звеньев;
p – оператор Лапласа.

По приведенному листингу можно получить не только переходную характеристику ПИД- регулятора, но и ПИ-регулятора, приняв Kd=0:

3. Оценка точности численного метода обратного преобразования Лапласа invertlaplace применительно к типовым объектам САУ

С учётом предостережений относительно применимости invertlaplace, приведенных в начале статьи, в дальнейшем изложении была доказана применимость метода к объектам с запаздыванием и самовыравниванием, а так же к регуляторам.

Остаётся до конца не выясненным вопрос точности численного решения. Для внесения ясности воспользуемся передаточной функцией (2) и следующим точным её преобразованием в переходную функцию, приведённую в [1]:

Получим следующий график:

Из графика видно, что погрешность численного метода для приведенного класса передаточных функций пренебрежимо мала (3*10^-15). Кроме того, погрешностью численного метода можно управлять, устанавливая значения mp.dps и шаг tt[i+1]-tt[i] (см. листинг).

4. Сравнительная оценка точности численного метода обратного преобразования Лапласа invertlaplace и численного метода обратного преобразования Фурье применительно к типовым объектам САУ

Построение переходной характеристики можно произвести на основе формулы обратного преобразования Фурье [1]:

где X(j∙ω)— Фурье-изображение оригинала x(t)

где Re(W(j∙ω))— вещественная частотная характеристика объекта регулирования.

В качестве верхнего предела интегрирования θв в расчете берется значение частоты ωс, при котором модуль Re(W(j∙ω)) уменьшается до некоторого малого значения (например, 0,05*K) и не превосходит это значение при дальнейшем возрастании ω.

Вначале определим верхний предел интегрирования в соотношении (5). Для этого воспользуемся передаточной функцией (1), предварительно избавившись от единичного воздействия, умножив правую часть на оператор p.

Из графика видно, что верхний предел интегрирования в соотношении (5) может быть принят равным 0.6, поскольку при дальнейшем увеличении частоты вещественная часть передаточной функции объекта управления сохраняет нулевое значение.

Используя (5), получим переходную характеристику объекта управления методом обратного преобразования Фурье:

Для сравнительной оценки точности обратного преобразования Лапласа и Фурье, воспользуемся точным преобразованием передаточной функции (1) объекта управления приведенном в [1]:

Из точного преобразования (6) вычтем по очереди обратное преобразование (1) Лапласа и обратное преобразование Фурье. Для построения графика, характеризующего сравнение точности обеих методов, составим следующий листинг программы:

Из графика следует, что численное обратное преобразование Лапласа является более стабильным, чем Фурье и, кроме этого, оно совпадает с точным решением.

Выводы

1. Проведен сравнительный анализ численных методов обратного преобразования Лапласа и Фурье, показана большая точность и стабильность обратного преобразования Лапласа.
2. Показаны возможности применения библиотеки mpmath Python для обратного преобразования Лапласа основных передаточных функций объектов и элементов САУ.

Источник

Обратное преобразование Лапласа

Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.

Содержание

Определение

Прямое преобразование Лапласа

Преобразованием Лапласа функции действительной переменной , называется функция комплексной переменной , такая что:

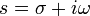
Правая часть этого выражения называется интегралом Лапласа.

Обратное преобразование Лапласа

Обратным преобразованием Лапласа функции комплексного переменного , называется функция действительного переменного, такая что:

где — некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича.

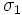
Двустороннее преобразование Лапласа

Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции участвуют значения x

Двусторонее преобразование Лапласа определяется следующим образом:

Дискретное преобразование Лапласа

Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.
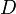
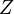
Различают -преобразование и -преобразование.

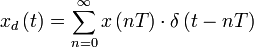
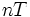
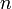
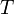
Пусть — решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени , где — целое число, а — период дискретизации.
Тогда применяя преобразование Лапласа получим:

Если применить следующую замену переменных: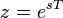
,
получим Z-преобразование:

Свойства и теоремы

,

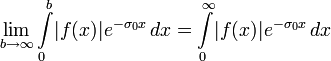
Преобразование Лапласа 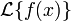существует в смысле абсолютной сходимости в следующих случаях:

Примечание: это достаточные условия существования.

Для существования обратного преобразования Лапласа достаточно выполнение следующих условий:

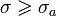
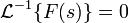
1. Если изображение F(s) — аналитичная функция для и имеет порядок меньше −1, то обратное преобразование для неё существует и непрерывно для всех значений аргумента, причём для

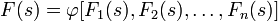
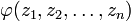
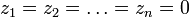
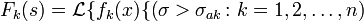
2. Пусть , так что аналитична относительно каждого z_k и равна нулю для , и , тогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.

Примечание: это достаточные условия существования.

Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов.

Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.

Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа.

Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала деленное на свой аргумент.

Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком.

Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, деленный на свой аргумент.

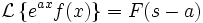
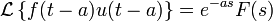
Теоремы о начальном и конечном значении (предельные теоремы):

, все полюсы в левой полуплоскости

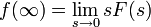
Теорема о конечном значении очень полезна, так как описывает поведение оригинала на бесконечности с помощью простого соотношения. Это, к примеру, используется для анализа устойчивости траектории динамической системы.

Умножение на число

Прямое и обратное преобразование Лапласа некоторых функций

Ниже представлена таблица преобразования Лапласа для некоторых функций.

Применения преобразования Лапласа

Преобразование Лапласа находит широкое применение во многих областях математики (операционное исчисление), физики и техники.

Связь с другими преобразованиями

Фундаментальные связи

Практически все интегральные преобразования имеют схожую природу и могут получаться одно из другого через выражения соответствия. Многие из них являются частными случаями других преобразований. Далее даны формулы, связывающие преобразования Лапласа с некоторыми другими функциональными преобразованиями.

Преобразование Лапласа-Карсона

Преобразование Лапласа-Карсона получается из преобразования Лапласа путём домножения его на комплексную переменную.

Двустороннее преобразование Лапласа

Двустороннее преобразование Лапласа 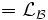связано с односторонним с помощью следующей формулы:

Преобразование Фурье

Непрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом s = iω :

Примечание: в этих выражениях опущен масштабирующий множитель 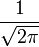, который часто включается в определения преобразования Фурье.

Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы.

Преобразование Меллина

Преобразование Меллина и обратное преобразование Меллина связаны с двусторонним преобразованием Лапласа простой заменой переменных. Если в преобразовании Меллина

Z-преобразование

Z-преобразование — это преобразование Лапласа решётчатой функции, производимое с помощью замены переменных:

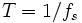
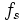
где — период дискретизации, а — частота дискретизации сигнала. Связь выражается с помощью следующего соотношения:

Преобразование Бореля

Интегральная форма преобразования Бореля идентична преобразованию Лапласа, существует также обобщённое преобразование Бореля, с помощью которого использование преобразования Лапласа распространяется на более широкий класс функций.

Библиография

См. также

Внешние ссылки

Преобразование Абеля | Преобразования Бесселя | Преобразование Бушмана | Преобразование Гильберта | Преобразование Конторовича — Лебедева | Преобразование Лапласа | Преобразование Мейера | Преобразование Мелера — Фока | Преобразование Меллина | Преобразование Нерейна | Преобразование Радона | Преобразование Стильтьеса | Преобразование Фурье | Преобразование Хартли | Преобразование Хенкеля

Полезное

Смотреть что такое «Обратное преобразование Лапласа» в других словарях:

обратное преобразование Лапласа — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN inverse Laplace transform … Справочник технического переводчика

Преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются… … Википедия

Лапласа преобразование — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и … Википедия

Преобразование Фурье — Преобразование Фурье операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие … … Википедия

Преобразование Радона — интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математика Иоганна Радона 1917 го года[1]. Важнейшее свойство преобразования Радона обратимость, то есть возможность… … Википедия

Преобразование — одно из основных понятий математики, возникающее при изучении соответствий между классами геометрических объектов, классами функций и т.п. Например, при геометрических исследованиях часто приходится изменять все размеры фигур в одном и… … Большая советская энциклопедия

Фурье преобразование — Преобразование Фурье операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие … … Википедия

Источник

2. Математическое описание систем автоматического управления ч. 2.9 — 2.13

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В предыдущих сериях:

В это части будут рассмотрены:

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.

Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)

Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1

Предположим, что уравнение динамики имеет вид:

где: — постоянные времени;
— коэффициент усиления.

Пусть известны отображения:

Найдем изображения для производных:

Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:

B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.

Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.

После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.

Пример

Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:

входное воздействие: — единичное ступенчатое воздействие.

Выполним преобразование Лапласа:

Подставим в уравнение динамики и получим уравнение динамики в изображениях:

Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:

2.10. Весовая и переходная функции звена (системы).

Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.

Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.

На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:

Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.

Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):

тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:

Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:

2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона

Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).

Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:

где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.

Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:

Переходя к пределам

если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:

где — вспомогательное время

Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:

Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:

2.12. Mетод переменных состояния.

До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)

В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2

В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:

Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:

где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;

Данная система уравнений может быть записана в матричной форме:

где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;

В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.

Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования

Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.

Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики

Пример решения задачи в форме коши.

Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:

Уравенение движение плунжера:

Где: – площадь плунжера, – жесткость пружины, – коэффициент вязкого трения, p – давление в камере.

Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда

Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:

Где: Q – расход в камеру, V — объем камеры.

Расход через дроссель:

Где: f– площадь дросселя, – давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:

Подставляем линеаризованную формул расхода в формулу давления:

Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:

Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:

Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.

Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:

Рисунок 2.12.5 Глобальный скрипт проекта.

Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)

Рисунок 2.12.6 Скрипт расчета модели в форме Коши.

Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7

Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)

Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10

На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.

2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно

Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:

Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:

2.13.1. Правая часть содержит только b₀*u(t)

В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.

Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:

Для перехода к форме Коши ведем новые переменные:

И перепишем уравнение относительно y»'(t):

Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:

Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:

2.13.2. Правая часть общего вида

Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:

Сделаем преобразования: перейдем к уравнениям динамики в изображениях:

Тогда можно представить уравнение в изображениях в виде:

Разделим уравнение в изображениях на произведение полиномов , получим:

Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что отображение величины . Тогда входная величина может быть в изображениях представлена как:

Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.

А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:

Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния :

А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:

Перейдем от изображения к оригиналам:

Если обозначить вектор , то мы получим уравнения переменных состояниях в матричной форме, где D = 0:

Пример:

Рисунок 2.13.1 Передаточная функция.

Имеется передаточная функция (рис. 2.13.1) в изображениях :

Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши

В изображения реакция системы связана с входным воздействие соотношением:

Разделим в последнем правую и левую часть на произведения , и введем новую перменную :

Полиномы N(s) и L(s) равны:

Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):

Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:

Или в матричной форме:

Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:

Перейдем от изображений к оригиналу:

Таким образом второе уравнение матричной системы выглядит так:

Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2

Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.

Источник