Что такое общая часть в математике

Задачи на части

Рассмотрим задачи, для решения которых некоторую величину можно принять за одну или несколько частей. При решении таких задач бывает полезно делать рисунки, облегчающие решение.

Задача 1. В двух коробках лежит 120 дисков — в первой коробке в 3 раза больше дисков, чем во второй. Сколько дисков лежит в каждой коробке?

Решение: Представим содержимое коробок в виде частей. Если диски, находящиеся во второй коробке, составляют 1 часть, то в первой коробке — 3 такие части. Сделаем схематический рисунок:

1) Сколько частей составляют 120 дисков?

2) Сколько дисков приходится на 1 часть?

3) Сколько дисков находится в первой коробке?

Ответ: 90 — в первой коробке, 30 — во второй.

Задача 2. Некто заплатил за книгу на 120 рублей больше, чем за тетрадь. Известно, что книга дороже тетради в 4 раза. Сколько стоит книга?

Решение: Представим стоимость в виде частей. Если стоимость тетради составляет 1 часть, то стоимость книги составляет 4 такие же части. Сделаем схематический рисунок:

2) 120 : 3 = 40 (рублей) — приходится на 1 часть.

3) 40 · 4 = 160 (рублей) — стоит книга.

Ответ: Книга стоит 160 рублей.

Задача 3. В первой коробке на 6 карандашей больше, чем во второй, а в двух вместе 30 карандашей. Сколько карандашей в каждой коробке?

Решение: Сделаем схематический рисунок:

1) Если из первой коробки вынуть 6 карандашей, в ней станет столько же карандашей, сколько и во второй:

2) Найдём число карандашей в каждой из коробок:

3) Теперь вернём 6 карандашей в первую коробку:

Ответ: В первой коробке 18 карандашей, во второй — 12.

Источник

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A₁, A₂ и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a₁, a₂ и т. д.

Границы совокупности обозначаются фигурными скобками < >.

А = <а, в, с, у>– А состоит из четырех элементов.

Записать совокупность Z согласных букв в слове «калькулятор»:

Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = , а Є N – элемент «а» принадлежит N.

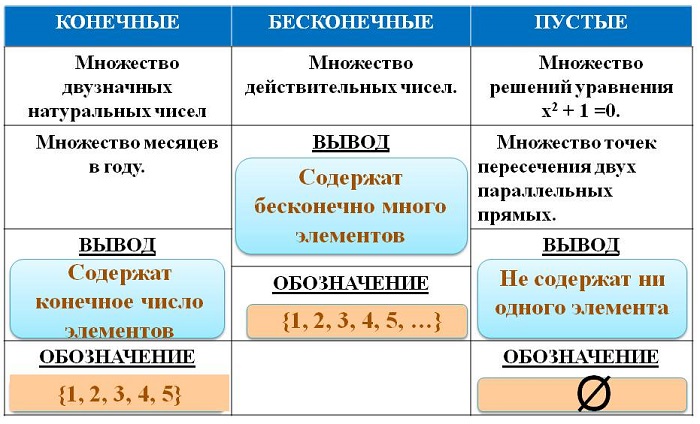
Выделяют три вида множеств:

пустые (обозначаются Ø) – не имеющие элементов.

Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

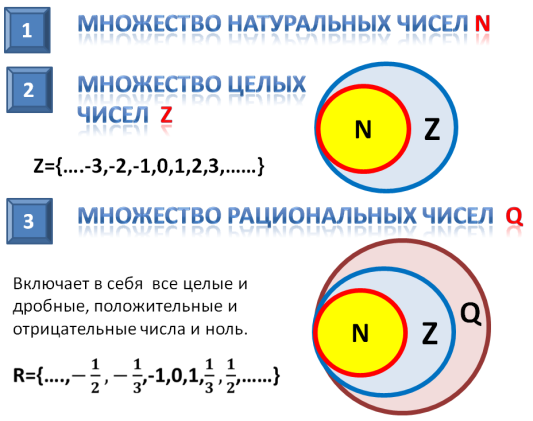
Множество натуральных чисел

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

Следовательно, N и Z являются подмножествами Q.

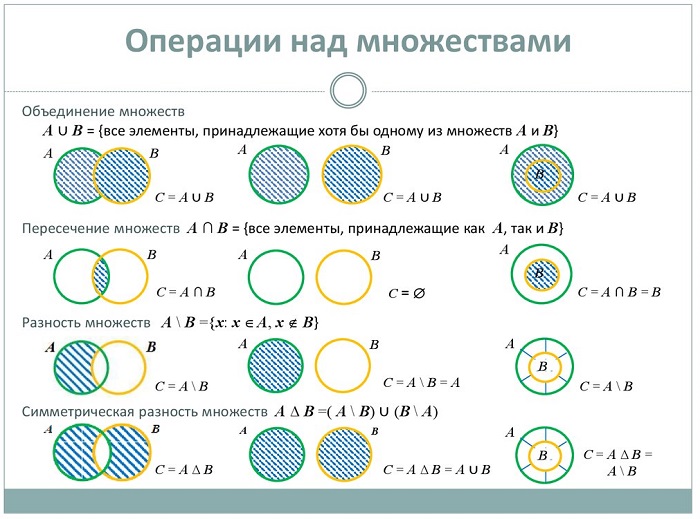
Операции над множествами

Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.

Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.

Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.

Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.

В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.

Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:

Объединение

Пересечение

Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.

Свойства операций над множествами

Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:

умножения S ∩ D = D ∩ S;

сложения S ∪ D = D ∪ S.

Ассоциативность – сочетательные законы:

умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);

сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).

Дистрибутивность – законы распределения:

умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);

умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);

сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).

если S ⊆ Fи F ⊆ J, то S ⊆ J;

если S ⊆ F и F ⊆ S, то S = F.

Идемпотентность объединения и пересечения:

О других свойствах операций можно узнать из картинки:

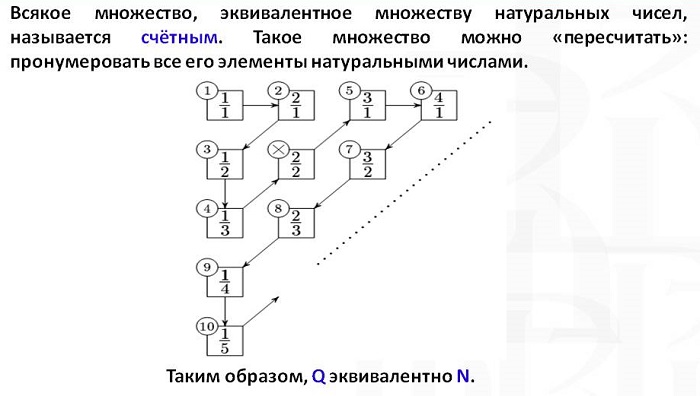
Счетные и несчетные множества

Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.

Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.

Источник

ru.knowledgr.com

Общая, вульгарная, или простая часть (примеры: и 17/3), состоит из нумератора целого числа, показанного выше линии (или перед разрезом), и знаменатель целого числа отличный от нуля, показанный ниже (или после) та линия.

Нумераторы и знаменатели также используются в частях, которые не распространены, включая составные части, сложные части и смешанные цифры.

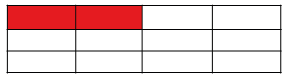
Нумератор представляет много равных частей, и знаменатель, который не может быть нолем, указывает, сколько из тех частей составляет единицу или целое. Например, в части 3/4, нумератор, 3, говорит нам, что часть представляет 3 равных части, и знаменатель, 4, говорит нам, что 4 части составляют целое. Картина вправо иллюстрирует или 3/4 пирога.

Фракционные числа могут также быть написаны, не используя явные нумераторы или знаменатели, при помощи десятичных чисел, знаков процента или отрицательных образцов (как в 0,01, 1%, и 10 соответственно, все из которых эквивалентны 1/100). Целое число, такое как номер 7 может считаться наличием неявного знаменателя одного: 7 равняется 7/1.

Другое использование для частей должно представлять отношения и представлять подразделение.

Таким образом часть 3/4 также используется, чтобы представлять отношение 3:4 (отношение части к целому) и подразделение 3 ÷ 4 (три разделенных четыре).

Словарь

Читая части это обычно на английском языке, чтобы объявить знаменатель, используя соответствующее порядковое числительное во множественном числе, если нумератор не один, как в «пятых» для частей с 5 в знаменателе. Таким образом 3/5 предоставлен как три пятых и 5/32 как пять тридцать секунд. Это обычно относится к знаменателям целого числа, больше, чем 2, хотя большие знаменатели, которые не являются полномочиями десять, часто предоставляются, используя количественное числительное. Таким образом 5/123 мог бы быть предоставлен как «пять сто двадцать третей», но часто «пять более чем сто двадцать три». Напротив, потому что один миллион власть десять, 6/1,000,000 обычно выражается как «шесть миллионных частей» или «шесть миллионных частей», а не как «шесть более чем один миллион».

Знаменатели 1, 2, и 4 являются особыми случаями. О части 3/1 можно говорить как три wholes. Знаменатель 2 выражен как половина (множественные половины); «−» минус или отрицательные три половины с тремя половинами. Часть 3/4 может быть или «тремя четвертями» или «тремя четвертями». Кроме того, начиная с большинства частей в функции прозы как прилагательные, фракционный модификатор написан через дефис. Это очевидно в стандартной прозе, в которой мог бы написать о «каждых двух десятых частях мили», «пробег четверти мили» или Компромисс С тремя пятыми. Когда нумератор части равняется 1, тогда слово, можно быть опущен, такие как «каждая десятая часть секунды» или «в течение заключительной четверти года».

В примерах 2/5 и 7/3, наклонную линию называют solidus или передовым разрезом. В примерах и, горизонтальную линию называют vinculum или, неофициально, «дробная черта». Когда с solidus столкнутся в части, спикер будет иногда разбирать его, объявляя его по как в примерах выше.

Формы частей

Простые, общие, или вульгарные части

Как с другими частями, знаменатель (b) не может быть нолем. Примеры включают, и 3/17.

Простые части могут быть положительными или отрицательными, надлежащими, или неподходящими (см. ниже). Составные части, сложные части, смешали цифры и десятичные числа (см. ниже), не простые части, тем не менее, если не иррациональный, они могут быть оценены к простой части.

Надлежащие и неподходящие части

Смешанные числа

Смешанная цифра (часто называемый смешанным числом, также названным смешанной частью), является суммой целого числа отличного от нуля и надлежащей части. Эта сумма подразумевается без использования любого видимого оператора такой как «+». Например, в обращении к двум всем пирогам и трем четвертям другого пирога, целые и фракционные части числа написаны друг рядом с другом:.

Это не должно быть перепутано с правилом алгебры подразумеваемого умножения. Когда два алгебраических выражения написаны друг рядом с другом, операция умножения, как говорят, «понята». В алгебре, например не смешанное число. Вместо этого умножение понято где.

Чтобы избежать беспорядка, умножение часто явно выражается. Так может быть написан как

Точно так же неподходящая часть может быть преобразована в смешанное число следующим образом:

Смешанные числа могут также быть отрицательными, как в, который равняется.

Отношения

Отношение часто преобразовывается в часть, когда оно выражено как отношение целому. В вышеупомянутом примере отношение желтых автомобилей ко всем автомобилям на партии 4:12 или 1:3. Мы можем преобразовать эти отношения в часть и сказать, что 4/12 автомобилей или 1/3 автомобилей в партии желтые. Поэтому, если человек беспорядочно выбрал один автомобиль на партии, то есть тот в трех шансах или вероятности, что это было бы желто.

Аналоги и «невидимый знаменатель»

Сложные части

:Not, который будет перепутан с частями, включающими Комплексные числа

В сложной части или нумератор, или знаменатель, или оба, является частью или смешанным числом, соответствуя подразделению частей. Например, и сложные части. Чтобы уменьшить сложную часть до простой части, рассматривайте самую длинную линию части как представление подразделения. Например:

Составные части

Десятичные дроби и проценты

Десятичные дроби могут также быть выражены, используя научное примечание с отрицательными образцами, такой как, который представляет 0.0000006023. Представление знаменателя. Деление на перемещает десятичную точку 7 мест налево.

Десятичные дроби с бесконечно многими цифрами направо от десятичного сепаратора представляют бесконечный ряд. Например, 1/3 = 0.333. представляет бесконечный ряд 3/10 + 3/100 + 3/1000 +.

Или простые дроби или десятичные дроби используются, часто вопрос вкуса и контекста. Простые дроби используются чаще всего, когда знаменатель относительно маленький. Умственным вычислением легче умножиться 16 на 3/16, чем сделать то же самое вычисление, используя десятичный эквивалент части (0.1875). И более правильно умножиться 15 на 1/3, например, чем это должно умножиться 15 каким-либо десятичным приближением одной трети. Денежная стоимость обычно выражается как десятичные дроби, например 3,75$. Однако, как отмечено выше, в преддесятичной британской валюте, шиллингам и пенсам часто давали форму (но не значение) части, как, например 3/6 (прочитанный «три и шесть&#187) значение 3 шиллингов и 6 пенсов, и наличие никаких отношений к части 3/6.

Особые случаи

Арифметика с частями

Как целые числа, части подчиняются коммутативным, ассоциативным, и дистрибутивным законам и правилу против деления на нуль.

Эквивалентные части

Используя эти правила, мы можем показать это = = =.

Простая дробь может быть уменьшена до самых низких условий, делясь и нумератор и знаменатель их самым большим общим делителем. Например, поскольку самый большой общий делитель 63 и 462 равняется 21, часть может быть уменьшена до самых низких условий, деля нумератор и знаменатель на 21:

Евклидов алгоритм дает метод для нахождения самого большого общего делителя любых двух положительных целых чисел.

Сравнение частей

Сравнение частей с тем же самым знаменателем только требует сравнения нумераторов.

Не необходимо определить ценность общего знаменателя, чтобы сравнить части. Этот короткий путь известен как «умножение креста» – Вы можете просто сравнить объявление и до н.э, не вычисляя знаменатель.

Умножьте вершину и основание каждой части знаменателем другой части, чтобы получить общего знаменателя:

Дополнение

Первое правило дополнения состоит в том, который только как количества может быть добавлен; например, различные количества четвертей. В отличие от количеств, таких как добавляющие трети к четвертям, должен сначала быть преобразован, чтобы любить количества, как описано ниже:

Вообразите карман, содержащий две четверти и другой карман, содержащий три четверти; всего, есть пять четвертей. Начиная с четырех четвертей эквивалентно одной (доллар), это может быть представлено следующим образом:

Добавление в отличие от количеств

Чтобы добавить части, содержащие в отличие от количеств (например, четверти и трети), необходимо преобразовать все суммы, чтобы любить количества. Легко решить выбранный тип части, чтобы преобразовать в; просто умножьте вместе эти два знаменателя (нижнее число) каждой части.

Для добавления четвертей к третям оба типа части преобразованы в двенадцатые, таким образом:.

Рассмотрите добавление следующих двух количеств:

Во-первых, новообращенный в пятнадцатые, умножаясь и нумератор и знаменатель три:. с тех пор равняется 1, умножение не изменяет ценность части.

Во-вторых, новообращенный в пятнадцатые, умножаясь и нумератор и знаменатель пять:.

Теперь можно заметить что:

Этот метод может быть выражен алгебраически:

И для выражений, состоящих из добавления трех частей:

Этот метод всегда работает, но иногда есть меньший знаменатель, который может использоваться (наименьшее количество общего знаменателя). Например, добавить и знаменатель 48 может использоваться (продукт 4 и 12), но меньший знаменатель 12 может также использоваться, будучи наименьшим количеством общего множителя 4 и 12.

Вычитание

Процесс для вычитания частей является, в сущности, тем же самым как тем из добавления их: найдите общего знаменателя и измените каждую часть на эквивалентную часть с выбранным общим знаменателем. У получающейся части будет тот знаменатель, и его нумератор будет результатом вычитания нумераторов оригинальных частей. Например,

Умножение

Умножение части другой частью

Чтобы умножить части, умножьте нумераторы и умножьте знаменатели. Таким образом:

Короткий путь для умножения частей называют «отменой». Эффективно ответ уменьшен до самых низких условий во время умножения. Например:

Умножение части целым числом

Так как целое число может быть переписано, как само разделено на 1, нормальные правила умножения части могут все еще примениться.

Этот метод работает, потому что часть 6/1 означает шесть равных частей, каждая из которых является целым.

Умножение смешанных чисел

Умножая смешанные числа, считают предпочтительным преобразовать смешанное число в неподходящую часть. Например:

Другими словами, совпадает с, делая 11 четвертей всего (потому что 2 пирога, каждое разделение в четверти делает 8 общих количеств четвертей), и 33 четверти, так как 8 пирогов, каждый сделанный из четвертей, составляют 32 четверти всего.

Подразделение

Чтобы разделить часть на целое число, Вы можете или разделить нумератор на число, если это идет равномерно в нумератор, или умножьте знаменатель на число. Например, равняется и также равняется, который уменьшает до. Чтобы разделить число на часть, умножьте то число на аналог той части. Таким образом.

Преобразование между десятичными числами и частями

Чтобы изменить простую дробь на десятичное число, разделите знаменатель на нумератор. Вокруг ответа на желаемую точность. Например, чтобы изменить 1/4 на десятичное число, разделитесь 4 на 1,00, чтобы получить 0.25. Чтобы изменить 1/3 на десятичное число, разделитесь 3 на 1,0000. и остановка, когда желаемая точность будет получена. Обратите внимание на то, что 1/4 может быть написан точно с двумя десятичными цифрами, в то время как 1/3 не может быть написан точно ни с каким конечным числом десятичных цифр.

Чтобы изменить десятичное число на часть, напишите в знаменателе 1, сопровождаемый столькими же нолей, сколько есть цифры направо от десятичной запятой и пишут в нумераторе все цифры в оригинальном десятичном числе, опуская десятичную запятую. Таким образом 12.3456 = 123456/10000.

Преобразование повторяющихся десятичных чисел к частям

Десятичные числа, в то время как возможно более полезный, чтобы работать с, выполняя вычисления, иногда испытывают недостаток в точности, которую имеют простые дроби. Иногда бесконечное десятичное число повторения требуется, чтобы достигать той же самой точности. Таким образом часто полезно преобразовать повторяющиеся десятичные числа в части.

Предпочтительный способ указать на повторяющееся десятичное число состоит в том, чтобы разместить бар по цифрам, которые повторяются, например 0. = 0,789789789 … Для повторения образцов, где повторяющийся образец немедленно начинается после десятичной запятой, простого подразделения образца тем же самым числом девяток как числа, которые это имеет, будут достаточны. Например:

В случае, если неповторяющийся набор десятичных чисел предшествует образцу (такой как 0,1523), мы можем написать его как сумму неповторения и повторения частей, соответственно:

Затем преобразуйте обе части в части и добавьте их использующий методы, описанные выше:

:1523/10000 + 987/9990000 = 1522464/9990000

Альтернативно, алгебра может использоваться, такой как указано ниже:

Части в абстрактной математике

В дополнение к имению большого практического значения части также изучены математиками, которые проверяют, что правила для частей, данных выше, последовательны и надежны. Математики определяют часть как приказанную пару (a, b) целых чисел a и b ≠ 0, для которого операционное дополнение, вычитание, умножение и разделение определены следующим образом:

Кроме того, отношение эквивалентности определено следующим образом:

, если и только если.

Эти определения соглашаются в каждом случае с определениями, данными выше; только примечание отличается.

Алгебраические части

Терминология, используемая, чтобы описать алгебраические части, подобна используемому для обычных частей. Например, алгебраическая часть находится в самых низких терминах, если единственные факторы, характерные для нумератора и знаменателя, равняются 1 и −1. Алгебраическую часть, нумератор которой или знаменатель или оба, содержат часть, такой как, называют сложной частью.

Термин элементарная дробь использован, анализируя рациональные выражения в суммы. Цель состоит в том, чтобы написать рациональное выражение как сумму других рациональных выражений со знаменателями меньшей степени. Например, рациональное выражение может быть переписано как сумма двух частей: +. Это полезно во многих областях, таких как интегральное исчисление и отличительные уравнения.

Радикальные выражения

Процесс рационализации двучленных знаменателей включает умножение вершины и основания части сопряженным из знаменателя так, чтобы знаменатель стал рациональным числом. Например:

Источник

Что такое общая часть в математике

В этой теме мы познакомимся с образованием долей, научимся их записывать, читать и сравнивать.

Доли появляются, если нам нужно разделить ЦЕЛОЕ на равные части, например, яблоко:

.

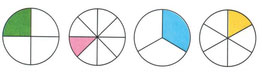
На доли можно разделить окружность:

Доля – это каждая из равных частей целого.

Название доли зависит от того, на сколько частей разделили целое.

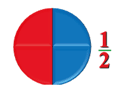
Половина

Например, яблоко разделили на две части, получилась половина яблока.

Любую долю можно записать как деление двух чисел. Мы разделили целое на две доли, каждую из долей мы можем записать в виде дроби, в которой черта обозначает знак деления.

Прочитать такую долю можно как ОДНА ВТОРАЯ.

Треть

Если целое разделили на три части, то получили ТРЕТЬ, третью часть.

Прочитать такую долю можно как ОДНА ТРЕТЬЯ.

Четверть

Если целое разделили на четыре части, получили ЧЕТВЕРТЬ, четвёртую часть.

Прочитать такую долю можно как ОДНА ЧЕТВЁРТАЯ.

Запись и чтение долей

одна пятая

одна шестая

одна восьмая

Сравнение долей

Для примера сравним две доли: одну шестую и одну третью.

Какая доля больше? Рассмотри рисунок:

Красным закрашены названные доли. Посмотри, какая доля больше? Одна третья.

Значит, одна третья часть БОЛЬШЕ, чем одна шестая часть.

Сравним ещё две доли: одну восьмую и одну четвёртую.

Какая доля больше? Рассмотри рисунок:

Красным закрашены названные доли. Посмотри, какая доля больше? Одна четвёртая.

Значит, одна четвёртая часть БОЛЬШЕ, чем одна восьмая часть.

Вывод: Чем долей больше, тем одна её часть МЕНЬШЕ.

Поделись с друзьями в социальных сетях:

Источник