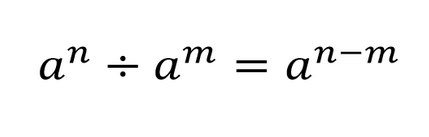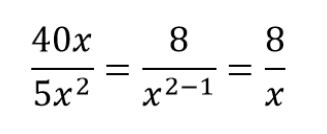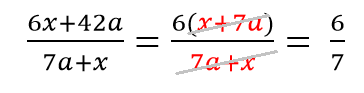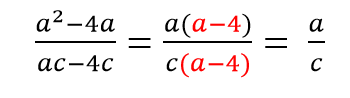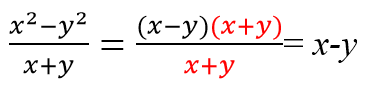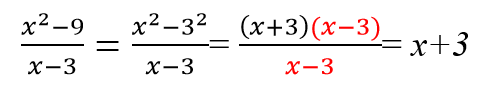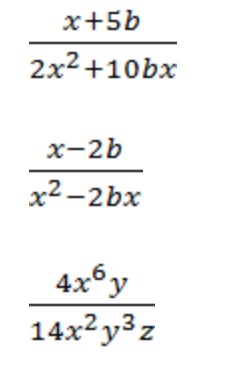Что такое общий множитель
Вынесение общего множителя за скобки
5 класс, 6 класс, 7 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие вынесения множителя за скобки
Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.
Есть несколько способов разложения многочлена на множители. Один из них — вынесение общего множителя за скобки.
Вынести общий множитель за скобки можно в выражениях, которые представляют из себя суммы, в которых каждое слагаемое является произведением, причем в каждом произведении есть один одинаковый для всех множитель. Он так и называется — общий множитель.
Вынесение общего множителя за скобки — это преобразование многочлена в произведение с помощью распределительного свойства умножения. Только в случае вынесения множителя за скобки это свойство применяется справа налево.
Формула вынесения общего множителя за скобки:
Покажем метод вынесения общего множителя за скобки на примере с цифрами:
Определение общего множителя для всех членов многочлена производится пошагово:
Если нам дано произведение 6 * 2 и 6 * 5, то мы можем вынести за скобки общий множитель 5. В чем состоит данное преобразование? Мы представляем исходное выражение как произведение общего множителя и выражения в скобках, которое содержит сумму всех исходных слагаемых, кроме общего множителя.
Итак, вынесем общий множитель 5 в 6 * 2 и 6 * 5 и получим 6 * (2 + 5).
Итоговое выражение — это произведение общего множителя 6 на выражение в скобках, которое является суммой исходных слагаемых без 6.
Так и получается: 6 * 2 + 6 * 5 = 6 * (2 + 5).
Правило вынесения общего множителя за скобки
Основное правило вынесения общего множителя за скобки
Чтобы вынести за скобки общий множитель, нужно записать исходное выражение в виде произведения общего множителя и скобок, которые включают в себя исходную сумму без общего множителя.
Алгоритм вынесения общего множителя за скобки:
Важно! В скобках должно быть столько одночленов, сколько их было в многочлене.
Это и есть итог нашего преобразования. Запись всего решения выглядит так:
Определить сразу, какой множитель является общим, получается не всегда. Иногда выражение нужно предварительно преобразовать, заменив числа и выражения тождественно равными им произведениями.
Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Вынесение минуса за скобки
Еще один случай, на котором следует обратить внимание — это вынесение за скобки минуса. Только мы выносим не сам знак, а минус единицу. Часто это помогает упростить выражение и сделать его проще.
Чтобы вынести минус за скобки, нужно записать перед скобками минус и в скобках записать все слагаемые с противоположными знаками:
Найдем решение для каждого выражения:
Поэтому между выражениями можно поставить знак равенства, потому что они равны одному и тому же значению:
Ставим минус и рядом в скобках записываем выражение с противоположным знаком у каждого слагаемого:
Как и в прошлом примере, здесь за скобки вынесен не минус, а минус единица.
Вынесение за скобки общего множителя: правило, примеры
В рамках изучений тождественных преобразований очень важна тема вынесения общего множителя за скобки. В данной статье мы поясним, в чем именно заключается такое преобразование, выведем основное правило и разберем характерные примеры задач.
Понятие вынесения множителя за скобки
Чтобы успешно применять данное преобразование, нужно знать, для каких выражений оно используется и какой результат надо получить в итоге. Поясним эти моменты.
В чем состоит данное преобразование? В ходе него мы представляем исходное выражение как произведение общего множителя и выражения в скобках, содержащего сумму всех исходных слагаемых, кроме общего множителя.
Правило вынесения общего множителя за скобки
Используя все сказанное выше, выведем основное правило такого преобразования:
Чтобы вынести за скобки общий множитель, надо записать исходное выражение в виде произведения общего множителя и скобок, которые включают в себя исходную сумму без общего множителя.
Определить сразу, какой множитель является общим, возможно не всегда. Иногда выражение нужно предварительно преобразовать, заменив числа и выражения тождественно равными им произведениями.
В выводах отметим, что преобразование путем вынесения общего множителя за скобки очень часто применяется на практике, например, для вычисления значения рациональных выражений. Также этот способ полезен, когда нужно представить выражение в виде произведения, например, разложить многочлен на отдельные множители.
Как правильно выносить общий множитель за скобки в алгебре
Понятие вынесения общего множителя за скобки
Разложить многочлен на множители — значит, преобразовать многочлен в произведение, которое равно этому многочлену.
Существует несколько методов в алгебре, позволяющих разложить многочлен на отдельные множители. Одним из наиболее распространенных способов является вынесение общего множителя за скобки. Такая методика часто встречается на уроках в средних классах.
Вынесение общего множителя за скобки представляет собой применение распределительного правила умножения с целью преобразования многочлена и получения в результате произведения.
В процессе вынесения множителя за скобки двучлен (ab + ac) примет вид произведения: a*(b + c)
Как происходит вынесение общего множителя за скобки
Определить общий множитель для каждого из членов, которые входят в состав многочлена, достаточно просто. Нужно следовать следующему алгоритму действий:
В качестве показательного примера можно разобрать порядок разложения многочлена на множители с помощью вынесения общего множителя за скобки:
В первую очередь обратим внимание на коэффициенты 20, 10 и 15 для определения наибольшего общего делителя. Таковым является число 5. Значит, 5 является общим множителем для каждого из коэффициентов.
Далее можно приступить к вычислению многочлена, который остался в скобках. При группировке требуется разделить каждый из членов начального многочлена на определенный ранее общий множитель с учетом его знака:
20 a 2 b c 2 5 a 2 c = 4 b c
10 a 3 c 5 a 2 c = 2 a
15 a 2 b 2 c 5 a 2 c = 3 b 2
В результате проделанной работы получим:
При вынесении общего множителя за скобки совершается действие, которое является обратным умножению одночлена на многочлен:
Основное правило
Основное правило, которое применимо при вынесении общего множителя за скобки: вынесение общего множителя за скобки заключается в записи начального выражения, как произведения общего множителя и скобок, содержащих начальную сумму за исключением общего множителя.
В результате вынесения общего множителя за скобки в них остается такое же количество одночленов, которое содержалось в исходном многочлене.
Например, имеется некое выражение:
Заметим, что это сумма из трех слагаемых и общего множителя в виде числа 4. Руководствуясь правилом вынесения общего множителя за скобки, преобразуем выражение:
Преобразование выполнено, запишем итоговый результат:
Не во всех случаях получается определить общий множитель. Например, перед вынесением общего множителя может потребоваться замена чисел и выражений на произведения, которые тождественно им равны.
Попробуем разложить на множители многочлен:
Пояснение на примерах
В числовом выражении требуется вынести общий множитель за скобки:
В первую очередь следует определить максимально возможный общий множитель для двух слагаемых 15 и 20. Таковым будет являться число 5. Исключим его из скобок:
15 + 20 = 5 ( 15 5 + 20 5 ) = 5 * ( 3 + 4 )
Выполним проверку. В процессе необходимо выполнить умножение общего множителя в виде числа 5 на каждое из слагаемых. В том случае, когда ответ верный, выражение примет вид 15 + 20:
5 * ( 3 + 4 ) = 5 × 3 + 5 × 4 = 15 + 20
Вынести за скобки общий множитель в выражении:
Заметим, что в условии задания записана сумма простых чисел 13 и 5. В связи с этим, такие числа можно разложить на единицу и самих себя:
Такие слагаемые не имеют общих множителей, за исключением единицы. С другой стороны, число 1 бессмысленно выносить за скобки. Выполним преобразования:
13 + 5 = 1 ( 13 1 + 5 1 ) = 1 ( 13 + 5 )
Дано выражение, в котором требуется вынести общий множитель за скобки:
Выполним замену вычитания на сложение:
−20 − 16 − 2 = −20 + (−16) + (−2)
Ответ можно записать в сокращенном виде:
Заметим, что если бы мы вынесли за скобки общий множитель в виде числа 2 без минуса, то получили бы ответ правильный, но не аккуратный:
Дано выражение, в котором требуется вынести за скобки общий множитель:
Выполним замену вычитания на сложение:
Выполним преобразования согласно правилу вынесения общего множителя за скобки:
Вынесение общего множителя за скобки
Преобразование математического выражения, в результате которого многочлен представлен произведением нескольких множителей и тождественен (т.е. равен) исходному, называют разложением многочлена на множители.
Чтобы вынести общий множитель за скобки, сначала нужно его найти.
Не забываем полезные лайфхаки для нахождения общего множителя:
Все четные числа делятся на два;
Число делится на три, если сумма составляющих его цифр делится на три
(например, нужно узнать, делится ли на 3 число 78;
7+8=15:3=5, соответственно, 78 делится на 3)
На 5 делятся числа, которые оканчиваются на 0 и 5
Часто в алгебраические выражения и тождества входят буквенные переменные. Например а, в, с, х, у и другие. И многоэтажные примеры в учебники алгебры из нагромождения букв и чисел приводят неподготовленного ученика в священный трепет.
Не стоит пугаться. Буквенная переменная это полноправный множитель, и с ним можно производить все действия, которые применимы к обычным числам: сокращать, выносить за скобки, складывать, возводить в степень и т.д.
Работа с многочленом ведется в определенном порядке.
1.Сначала преобразуем числовые коэффициенты. Определяем, на какое наибольшее целое число (наибольший общий делитель) делятся числовые коэффициенты каждого входящего в уравнение одночлена без остатка.
Определили, что все числовые коэффициенты делятся на 4.
2. Затем находим общие буквенные коэффициенты для всех одночленов многочлена и выносим их за скобки в наименьшей степени.
В нашем примере 8а2+12аb-4a, общим буквенным коэффициентом является а в наименьшей степени 1. Выносим за скобки общий буквенный и определенный на предыдущем этапе общий числовой коэффициенты
NB! Чтобы проверить правильность проведенных преобразований, нужно умножить вынесенный за скобки одночлен на многочлен в скобках. В результате должно получиться исходное выражение.
А сейчас, чтобы закрепить тему «Вынесение за скобки общего множителя», решим пример из учебника «Алгебра» для 7 класса под редакцией Мерзляка А. Г.
Как сокращать алгебраические дроби?
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.
Сокращение дробей с буквами и степенями проходит в три этапа:
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
Пример сокращения дроби со степенями и буквами:
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
| ❌ Так нельзя | ✅ Так можно |
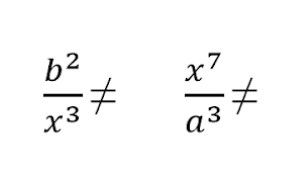 |  |
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
Получаем сокращенную дробь.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.
Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
| Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен. |
Пример 1.
Пример 2.
Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.
Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
Примеры сокращения дробей с помощью формул сокращенного умножения:
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.