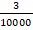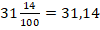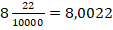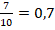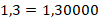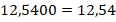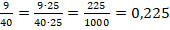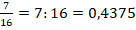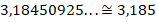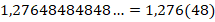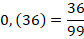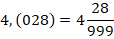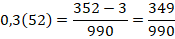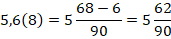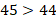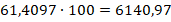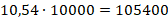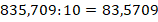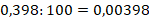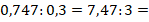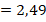Что такое обыкновенная десятичная дробь
Понятие десятичной дроби
В данной публикации мы рассмотрим, что из себя представляет десятичная дробь, как она пишется и читается, какой обыкновенной дроби соответствует и в чем заключается ее основное свойство. К теоретическому материалу прилагаются примеры для лучшего понимания.
Определение десятичной дроби
Десятичная дробь – это особый вид записи обыкновенной дроби, знаменатель которой равен 10, 100, 1000, 10000 и т.д.
Такие дроби вместо привычного варианта написания ( с числителем, знаменателем и черточкой-разделителем), принято записывать так: 0,3 ; 2,6 ; 5,62 ; 7,238 и т.д.
Десятичные дроби бывают двух типов:
Запись десятичной дроби
Десятичная дробь состоит из целой и дробной частей, между которыми находится десятичный разделитель – в виде запятой или точки.
Соответствие десятичной дроби обыкновенной:
Примеры:
, т.к. после запятой одна цифра.
, т.к. после запятой одна цифра.
, т.к. после запятой две цифры.
, т.к. после запятой три цифры.
Примечание: Если в десятичной дроби сразу после запятой идут нули и затем только цифры, то в виде обыкновенной дроби это выглядит так: числитель – только цифры без нулей, знаменатель – единица и количество нулей, соответствующее количеству цифр после запятой.
Например:
Чтение десятичной дроби
Читается десятичная дробь следующим образом: сначала произносится целая часть с добавление слова “целых”, затем дробная – с указанием разряда, который зависит от количества цифр после запятой:
Например:
Основное свойство десятичной дроби
Величина десятичной дроби не изменится, если справа к ней добавить любое количество нулей. Т.е. если такие нули встречаются, их можно просто отбросить (только те нули, которые расположены справа от цифр в дробной части).
Например:
Десятичные дроби: определения, запись, примеры, действия с десятичными дробями
Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.
Что такое десятичная запись дробных чисел
Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.
Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.
Определение десятичных дробей
Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:
Десятичные дроби представляют собой дробные числа в десятичной записи.
О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.
Как правильно читать десятичные дроби
Что такое разряды в десятичных дробях
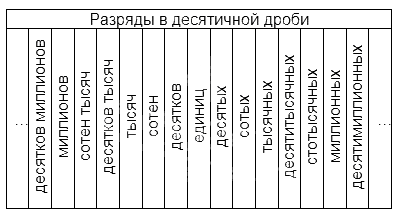
Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:
Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.
Что такое конечные десятичные дроби
Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:
Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.
Основные виды бесконечных десятичных дробей: периодические и непериодические дроби
Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.
Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.
В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.
Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.
Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.
Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.
Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.
К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.
Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.
Основные действия с десятичными дробями
С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.
Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.
Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.
Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.
Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.
Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.
Положение десятичных дробей на оси координат
Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.
Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.
Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.
Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.
Десятичная дробь
Десятичные дроби: определение, сложение, вычитание, умножение, деление, сравнение
Десятичная дробь является частным случаем обыкновенных дробей (у которой знаменатель кратен 10).
Определение
Десятичными называют дроби, знаменатели которых представляют собой числа, состоящие из единицы и некоторого количества следующих за нею нулей. То есть это дроби со знаменателем 10, 100, 1000 и т.д. Иначе десятичную дробь можно охарактеризовать как дробь со знаменателем 10 или одной из степеней десятки.
 ,
,  ,
, 
Десятичная дробь записывается иначе, чем обыкновенная. Операции с этими дробями также отличны от операций с обыкновенными. Правила действий над ними в значительной мере приближены к правилами действий над целыми числами. Этим, в частности, обусловлена их востребованность при решении практических задач.
Представление дроби в десятичной записи
В записи десятичной дроби нет знаменателя, в ней отображено число числителя. В общем виде запись десятичной дроби осуществляется по такой схеме:
где Х – целая часть дроби, Y – ее дробная часть, «,» – десятичная запятая.
Для правильного представления обыкновенной дроби в виде десятичной требуется, чтобы она была правильной, то есть с выделенной целой частью (если это возможно) и числителем, который меньше знаменателя. Тогда в десятичной записи целая часть записывается до десятичной запятой (Х), а числитель обыкновенной дроби – после десятичной запятой (Y).
Если в числителе представлено число с количеством знаков, меньшим, чем количество нулей в знаменателе, то в части Y недостающее количество знаков в десятичной записи заполняется нулями впереди цифр числителя.
Пример:
Если обыкновенная дробь меньше 1, т.е. не имеет целой части, то для Х в десятичном виде записывают 0.
В дробной части (Y), после последнего значимого (отличного от нуля) разряда, может быть вписано произвольное количество нулей. На значение дроби это не влияет. И наоборот: все нули в конце дробной части десятичной дроби можно опустить.
Прочтение десятичных дробей
Часть Х читается в общем случае так: «Х целых».
Часть Y прочитывается в соответствии с числом в знаменателе. Для знаменателя 10 следует читать: «Y десятых», для знаменателя 100: «Y сотых», для знаменателя 1000: «Y тысячных» и так далее… 😉
Более корректным считается другой подход к прочтению, основанный на подсчете количества разрядов дробной части. Для этого нужно понимать, что дробные разряды расположены в зеркальном отражении по отношению к разрядам целой части дроби.
Наименования для правильного прочтения приведены в таблице:
Исходя из этого, прочтение должно опираться на соответствие наименованию разряда последней цифры дробной части.
Перевод произвольной обыкновенной дроби в десятичную
Если в знаменателе обыкновенной дроби стоит 10 или какая-нибудь степень десятки, то перевод дроби выполняется как описано выше. В остальных ситуациях необходимы дополнительные преобразования.
Существует 2 способа перевода.
Первый способ перевода
Числитель и знаменатель необходимо домножить на такое целое число, чтобы в знаменателе было получено число 10 или одна из степеней десятки. А далее дробь представляется в десятичной записи.
Этот способ применим для дробей, знаменатель которых раскладывается только на 2 и 5. Так, в предыдущем примере 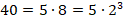
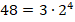
Второй способ перевода
2-й способ заключается в делении числителя на знаменатель в
Правило деления в столбик, приводящее в результате к десятичной дроби, описано ниже (см. Деление десятичных дробей).
Перевод десятичной дроби в обыкновенную
Для этого следует ее дробную часть (справа от запятой) записать в виде числителя, а результат прочтения дробной части – в виде соответствующего числа в знаменателе. Далее, если это возможно, нужно сократить полученную дробь.
Конечная и бесконечная десятичная дробь
Конечной называют десятичная дробь, дробная часть которой состоит из конечного количества цифр.
Выше все приведенные примеры содержат именно конечные десятичные дроби. Однако не всякую обыкновенную дробь возможно представить в виде конечной десятичной. Если 1-й способ перевода для данной дроби не применим, а 2-й способ демонстрирует, что деление невозможно завершить, значит, получена может быть только бесконечная десятичная дробь.
В полном виде бесконечную дробь записать невозможно. В неполном же виде такие дроби можно представить:
Периодической называется дробь, у которой после запятой можно выделить повторяющуюся бесконечно последовательность цифр.
Остальные дроби называются непериодическими. Для непериодических дробей допустим только 1-й способ представления (округление).
Пример периодической дроби: 0,8888888… Здесь налицо повторяющаяся цифра 8, которая, очевидно, будет повторяться до бесконечности, поскольку нет оснований предполагать иное. Эта цифра называется периодом дроби.
Периодические дроби бывают чистыми и смешанными. Чистой является десятичная дробь, у которой период начинается непосредственно после запятой. У смешанной дроби до периода после запятой имеется 1 или больше цифр.
54,33333… – периодическая чистая десят.дробь
2,5621212121… – периодическая смешанная дробь
Примеры записи бесконечных десятичных дробей:
Во 2-м примере показано, как правильно оформлять период в записи периодической дроби.
Перевод периодических десятичных дробей в обыкновенные
Для перевода чистой периодической дроби в обыкновенную ее период записывают в числитель, а в знаменатель пишут число, состоящее из девяток в количестве, равном количеству цифр в периоде.
Смешанная периодическая десятичная дробь переводится следующим образом:
Сравнение десятичных дробей
Десятичные дроби сравнивают первоначально по их целым частям. Больше та дробь, у которой больше ее целая часть.
Если целые части одинаковы, то сравнивают цифры соответствующих разрядов дробной части, начиная с первого (с десятых). Здесь действует тот же принцип: больше та из дробей, у которой больше разряд десятых; при равенстве цифр разряда десятых сравнивают разряды сотых и так далее.
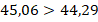
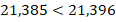
Сложение и вычитание десятичных дробей
Десятичные дроби складывают и вычитают так же, как и целые числа, записав соответствующие цифры друг под другом. Для этого нужно, чтобы друг под другом находились десятичные запятые. Тогда единицы (десятки и т.д.) целой части, а также десятые (сотые и т.д.) дробной окажутся в соответствии. Недостающие разряды дробной части заполняют нулями. Непосредственно процесс сложения и вычитания осуществляется так же, как и для целых чисел.
Примеры:
Умножение десятичных дробей
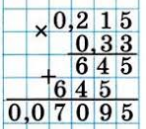
Для умножения десятичных дробей нужно записать их друг под другом, выровняв по последней цифре и не обращая внимания на местоположение десятичных запятых. Затем нужно перемножить числа так же, как и при умножении целых чисел. После получения результата следует пересчитать количество цифр после запятой в обоих дробях и отделить запятой в результирующем числе суммарное количество дробных разрядов. Если разрядов не хватает, то они заменяются нулями.
Умножение и деление десятичных дробей на 10 n
Примеры:
Деление десятичной дроби и целого числа на целое число и на десятичную дробь
Деление в столбик десятичной дроби на целое число выполняется аналогично делению двух целых чисел. Дополнительно требуется только учет положения десятичной запятой: при сносе цифры разряда, за которым следует запятая, необходимо поставить запятую после текущей цифры формируемого ответа. Далее нужно продолжать делить до получения нуля. Если знаков в делимом для полного деления недостает, в их качестве следует использовать нули.
Аналогично делятся в столбик 2 целых числа, если снесены все цифры делимого, а полное деление еще не завершено. В этом случае после сноса последней цифры делимого ставится десят.запятая в формирующемся ответе, а в качестве сносимых цифр используют нули. Т.е. делимое здесь, по сути, представляют как десятичную дробь с нулевой дробной частью.
Пример:
Графическое представление десятичных дробей
Графически десятичные дроби изображаются посредством координатной прямой. Для этого единичные отрезки делят дополнительно на 10 равных долей подобно тому, как на линейке откладываются одновременно сантиметры и миллиметры. Это обеспечивает точное отображение десятичных дробей и возможность объективного их сравнения.
Чтобы дольные деления на единичных отрезках были одинаковыми, следует тщательно продумывать длину самого единичного отрезка. Она должна быть такой, чтобы можно было обеспечить удобство дополнительного деления.
Десятичные дроби — для чайников
Действия с десятичными дробями – деление умножение, сложение, вычитание, сравнение. Разбор примеров.
Между прочим, большинство ошибок на экзаменах происходят как раз из-за незнания простейших действий вроде этих.
Так что читай эту статью и отрабатывай скиллы.
Десятичные дроби — коротко о главном
1. Определение
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени.
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
3. Свойства десятичных дробей
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
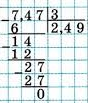
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
Деление десятичных дробей друг на друга
Десятичные дроби — подробнее
Конечно, ты знаешь, что такое обыкновенная дробь. Например, \( \displaystyle \frac<1><3>,\ \frac<1><4>,\frac<5><112>\).
Наравне с приведенными выше дробями существуют дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) и т.д.
Такие дроби можно записать намного удобнее и более кратко, то есть:
Данного вида дроби называются десятичными. Иными словами:
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).
Ты наверняка знаешь, что каждая цифра после запятой имеет свое название. На всякий случай напомню тебе про них, чтобы в дальнейшем мы говорили на одном языке:
Это огромное число читается по следующему алгоритму:
А теперь прочитаем все вместе – «\( 46\) целых одна тысяча двести тридцать четыре десятитысячные». Разобрался? Переходим к визуализации полученных знаний!
Итак, небольшая тренировка на понимание, что такое эта десятичная дробь! Нарисуй квадрат \( 10\) на \( 10\) и закрась какую-нибудь его часть равную:
Справился? Проверяем, что у тебя получилось.
Во-первых, квадрат \( 10\) на \( 10\) состоит из \( 100\) клеточек. Соответственно, \( 0.05\) – \( 5\) клеточек из \( 100\); \( 0,4\) – \( 40\) клеточек из \( 100\) и так далее.
С понятиями разобрались, теперь научимся переводить из десятичной дроби в обыкновенную и обратно.
Перевод из десятичной дроби в обыкновенную и обратно
Уверена, что ты с легкостью справился! А как насчет обратного перевода? Из обыкновенных в десятичные?
Попробуй свои силы на вот этих дробях:
Если ты со всем справился, можешь пропускать следующий абзац, а если где-то допустил ошибку, внимательно прочти о том, как легко и 100% правильно переводить дроби из обыкновенных в десятичные.
Разобрался? Посмотри еще раз эту маленькую «инструкцию»:
Я думаю, ты во всем-всем разобрался! Потренируемся? Попробуй поработать еще с вот этими дробями:
Виды десятичных дробей
Десятичная дробь может быть:
Поговорим сначала о конечных дробях.
Конечная десятичная дробь
Само собой понятно, что дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) являются конечными, ведь знаменатель дроби уже представлен как единица с последующими нулями, и поэтому мы сразу можем сказать, что данную обыкновенную дробь можно перевести в конечную десятичную. А что ты скажешь насчет этой дроби: \( \displaystyle \frac<1><4>\)? Ее знаменатель далеко не единица с последующими нулями, но ты четко знаешь, что у нее есть десятичный «аналог»:
То есть, чтобы определить, можно ли перевести дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число, такое, чтобы знаменатель стал равен \( 10\), \( 100\), \( 1000\) и так далее.
Усвоил? Постарайся представить в виде конечной десятичной дроби следующие обыкновенные дроби:
Сравним наши ответы:
Справился? Молодец. Выходим на новый уровень и переходим к бесконечным десятичным дробям.
Бесконечная десятичная дробь
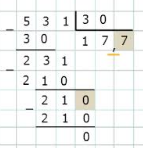
Итак, бери калькулятор и дели \( 1\) на \( 17\). Поделил? Ты получил \( 0,05882352941\) и дальше окошко калькулятора не показывает… Это тоже является десятичной дробью, только данная десятичная дробь является бесконечной. Ты сейчас скажешь, а как же наше определение?
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).
Все очень просто и никаких противоречий с определением нет. В данном случае нам необходимо привести наш знаменатель к \( <<10>^
Бесконечной десятичной дробью называется обыкновенная дробь, в записи которой после запятой содержится бесконечное количество цифр.
Как правило, в задачах, где встречаются бесконечные десятичные дроби, просят указать ответ либо с округлением (например, до десятых, или до сотых), либо записать в виде обыкновенной дроби, то есть как \( \displaystyle \frac<1><17>\).
Подумай, какой самый популярный пример можно привести на тему «бесконечная десятичная дробь»? Правильно! Число \( \pi \) является бесконечной десятичной дробью. Во всем мире люди договорились, что для решения математических задач принято, что \( \pi =3,14\), но это далеко не так. Число \( \pi \) не имеет определенного завершения. Оно настолько бесконечно, что ежегодно в мире проводятся соревнования по запоминанию числа \( \pi \). Мировой рекорд по запоминанию знаков числа \( \pi \) после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки! Все 67 890 знаков после запятой мы приводить не будем, а приведем несколько сокращенную запись:
Думаю, этого хватит, чтобы оценить «масштабы» данного числа.
Наравне с бесконечными десятичными дробями существуют периодические десятичные дроби. Они так же не имеют конца, но последующие числа в них повторяются, например, попробуй перевести в десятичную дробь \( \displaystyle \frac<1><3>\). Что у тебя получилось?
Чтобы не повторять число \( 3\) много много раз, решили говорить «ноль целых и три в периоде», так как тройка будет повторяться после запятой бесконечное число раз. Из этого умозаключения следует определение:
Дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр.
Чтобы кратко записать такую дробь, период (повторяющиеся цифры после запятой) пишут в скобках:
\( \displaystyle \frac<1><3>=0,\underbrace<3>_<период>33333333….=0,\left( 3 \right)\)
\( \displaystyle \frac<1><7>=0,\underbrace<142857>_<<период>>\underbrace<142857>_<период>142…=0,\left( 142857 \right)\)
Важно, что период не может начинаться слева от запятой:
\( \displaystyle \frac<100><7>=\underbrace<14,2857>_<не период>1428571428571…=14,\left( 285714 \right)\).

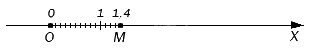
 ,
,  ,
,