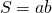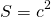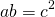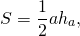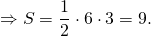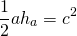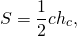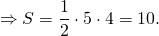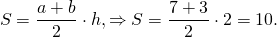Что такое одинаковые фигуры
Какие две фигуры называют равными?
Ответ или решение 2
Равными называются такие фигуры, которые можно совместить, воспользовавшись каким-либо видом движения (центральная и осевая симметрия, поворот и параллельный перенос).
В таких фигурах все стороны и углы соответственно равны.
Например, если даны треугольники ABC и A₁B₁C₁, то они равны в том случае, если соблюдается равенство сторон (AB = A₁B₁, BC = B₁C₁, AC = A₁C₁) и углов (угол A = угол A₁, угол B = угол B₁, угол C = угол C₁).
Также в равных фигурах равны и соответствующие точки и линии. Например, в тех же равных треугольниках ABC и A₁B₁C₁ будут равны биссектрисы, медианы, высоты, радиусы вписанной и описанной окружностей, центроиды и т.д.
Признаки равенства фигур
Геометрические фигуры считаются равными, если они являются точной копией друг друга, то есть должны выполняться следующие условия:
Что значит одинакова форма фигур
Говоря о форме фигуре, подразумевается в первую очередь класс геометрических фигур, а так же количество углов, направление выпуклостей (вогнутостей) и прочие визуальные детали контура плоской фигуры.
Почему важно совпадение размеров фигур
Что, если отличия в размерах визуально мало заметны? Тогда необходимо произвести точные замеры обоих фигур. Также равенство размеров разделяет понятия подобных и равных фигур. К примеру, 2 квадрата с разной площадью будут подобными, но не равными (имеется ввиду, когда один больше другого).
Что понимается под «наложением» фигур друг на друга
Иногда сделать точные замеры сложно. Особенно, если фигура образована замкнутой произвольной кривой или ломаной линией. Тогда нужно найти способ, чтобы наложить одну фигуру на другую.
Так, если они нарисованы на листе бумаги, нужно вырезать одну из них точно по контуру и положить поверх другой. Можно ее поворачивать в любом направлении и даже переворачивать. Если найдется способ совместить эти фигуры так, чтобы они совпали точно по контурам, значит они равны.
Всегда ли можно доказать равенство фигур
Иногда сделать это не возможно. Например, если речь идет о прямых. Все они бесконечны. То же касается и лучей.
Равные фигуры
Цель: формирование понятия “равные фигуры”.
1. Организационный момент
Вступительное слово учителя.
Она очень запутанная, на ней отмечено множество островов, чтобы запутать искателей, но нужно попасть на остров, на котором спрятаны сокровища. Чтобы его найти, нам нужно будет преодолеть множество препятствий. Вы готовы? Тогда в путь.
Путешествовать мы будем на корабле.
Отправляемся на первый остров.
Итак, следуя нашей карте, мы оказались на острове под названием “Устный счет”. И чтобы двинуться дальше, нам необходимо выполнить задания:
— назови соседей чисел: 3, 6, 8;
— реши пример по числовому отрезку.
3. Актуализация знаний
Следующий остров, встретившийся нам на пути, это “Геометрический остров”. Он таит в себе свои тайны и загадки, которые нам необходимо раскрыть!
— Ребята нужно вспомнить и нарисовать все известные нам геометрические фигуры. (Круг, квадрат, ромб, овал, прямоугольник)
— Посмотрите на рисунок, какие фигуры изображены?
— По каким признакам можно разбить все фигуры на группы? (Цвет, форма, размер). Назови эти группы.
4. Ознакомление с новым материалом
Мы удачно справились с заданием и можем отправиться на следующий остров. На третьем острове я нашла тайные послания для нас с вами. У каждого на парте есть конверт. Давайте откроем их и посмотрим, какое на этот раз испытание нас ждёт. (В каждом конверте находятся большой и маленький зеленый квадрат, большой и маленький синий треугольник, большой и маленький желтый прямоугольник, два красных круга одинакового размера)
— Ребята, вспомним, по каким признакам делятся все фигуры? (Цвет, форма, размер)
Задание: разбейте по парам фигуры, находящиеся в конверте, так, чтобы менялся только один признак – размер.
— Смогли ли вы разбить все предметы по парам? (Нет)
— Почему? (Потому что два круга одинаковы по размеру, цвету и форме)
— Докажите, что эти фигуры одинаковы. (Наложением)
— Давайте подумаем, как можно такие фигуры назвать? (Из предложенных вариантов учитель выбирает понятие “равные фигуры”)
— Итак, ребята, тема нашего урока “Равные фигуры”. (Тема фиксируется на доске)
Давайте поближе познакомимся с ними. Для этого нам нужно отправиться на следующий остров, который так и называется: “Равные фигуры”.
Прибыв на остров, я сразу заметила на песке различные фигуры, зарисовала их, так как волна могла в любой момент их смыть.
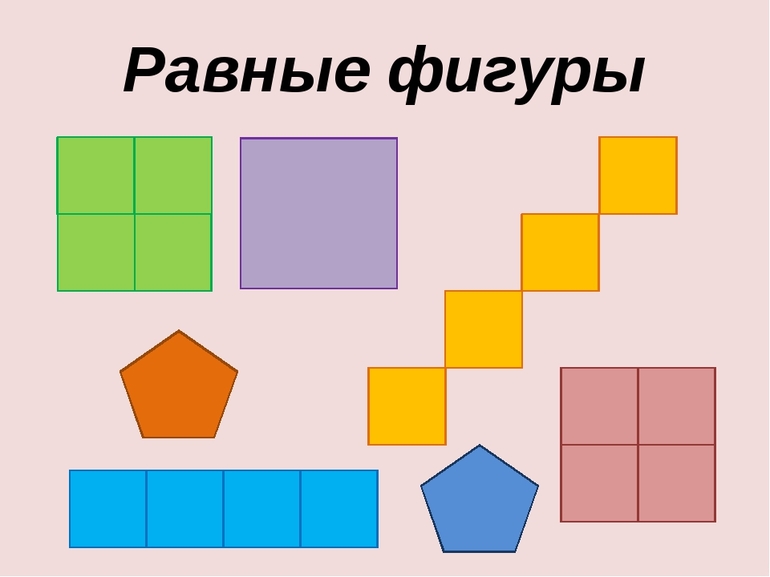
— Посмотрите на доску, вот эти фигуры:
— Если среди них равные? (Дети сначала определяют визуально равные фигуры, затем к доске вызывается ученик)
— Как мы узнаем, действительно эти фигуры равны или нет? (Путем наложения одной фигуры на другую). Выполняется практическое действие.
— Итак, какие же фигуры мы можем назвать равными? (Равными фигурами являются те, которые совпадают при наложении).
— Определим, какие признаки у равных фигур должны совпадать.
Под темой урока на доске фиксируется краткая запись рассуждений детей.
Ф
Ф
РР
Цили
Ц
(Равные фигуры всегда одинаковой формы и одинакового размера, а цвет может различаться)
Далее к доске приглашаются три ученика, каждому учитель выдаёт большую модель фигуры. Весь класс участвует в обсуждении.
— Как вы считаете, 1 и 2 фигуры – равные?
— Как мы это проверим? (Ученики совмещают фигуры и убеждаются, что они равны)
— А как вы думаете, 2 и 3 фигуры равны? (Выполняется аналогичная работа)
— Ребята, а 1 и 3 фигура равны?
— Почему? (Они обе равны фигуре 2, значит, равны друг другу)
— Давайте проверим наложением.
Ребята делают вывод, учитель кратко фиксирует на доске 1=2 и 2=3, то 1=3 (Если первая фигура равна второй, а вторая третьей, то первая фигура равна третьей)
— У меня возникла проблема, а если я не могу наложить фигуры, например, они нарисованы в тетради, как проверить, равны они или нет? (Можно посчитать по клеткам)
Отправляемся на следующий остров.
5. Первичное закрепление
Работа с учебником.
1) Стр. 36 №1. Найди равные фигуры и раскрась их одинаковым цветом. Работа выполняется по вариантам:
— Ребята, и с этим заданием вы справились, но продолжить наше путешествие мы не можем, корабль наткнулся на риф, нам необходимо его снова собрать. Потому что по карте последний остров именно тот, который нам нужен!
6. Повторение пройденного
Вы сегодня были храбры и не боялись сложных испытаний, которые встречались нам на островах. И в награду за это вы можете стать учителями-капитанами корабля. Но быть капитаном не просто, вам нужно многое знать и уметь, поэтому постарайтесь справиться со следующими заданиями:
1) Учащимся предлагается стать учителем: придумать задание к рисунку, проконтролировать выполнение, оценить.
2) Раздаются карточки. Нужно найти все ошибки. Взаимопроверка по парам.
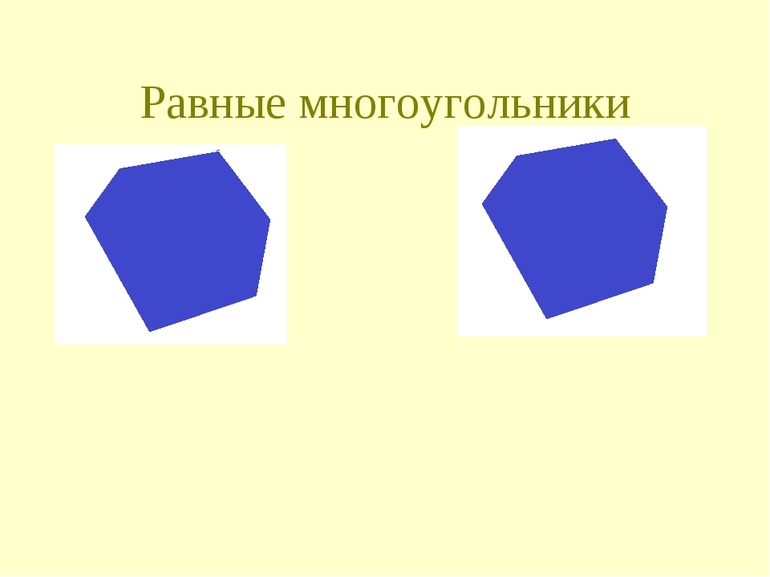
Равные многоугольники
По определению равные фигуры должны быть во всём одинаковыми, включая площадь, длину сторон, размер углов и другие параметры. Чтобы рассмотреть всё из них, уйдёт много времени, да это и не нужно, ведь они взаимозависимы. Хорошим примером будет самый простой многоугольник — треугольник. Существует несколько правил, по которым можно определить, равны ли 2 треугольника между собой или нет:
Нельзя путать первое условие с тремя углами. Ведь если в треугольнике равны 3 угла, они необязательно будут равными, но будут подобными.
Названия условий достаточно точно описывают критерии, по которым можно определить одинаковые 2 треугольника или нет. Из них следует, что необязательно знать все параметры: часто хватает только нескольких из них для определения «равности».
В большинстве случаев определить одинаковость других фигур гораздо сложнее, нежели треугольников. К счастью, чаще всего в школьной геометрии такой класс задач не рассматривают или даются дополнительные данные, помогающие с решением.
Например, доказательство «равности» для четырёхугольника сложнее, да и почти не встречается. Но если по условию сказано, что четырёхугольник не произвольный, а имеет прямые углы, задача становится проще. В таком случае рассматривается прямоугольник. А для него достаточно, чтобы 2 не противолежащие стороны были равны.
Если указано ещё и условие, что прямоугольник является квадратом, достаточно указать, что у двух таких фигур совпадает по длине одна сторона и уже этого будет достаточно.
Равность правильных фигур
Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат. Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы. При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».
Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.
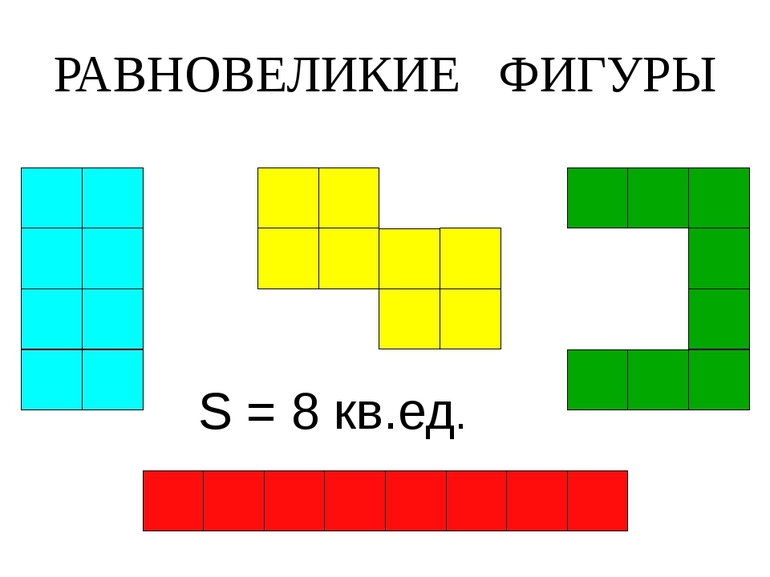
Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.
Вычисление площади треугольника
Чаще всего приходится работать с прямоугольными треугольниками. Их площадь вычислить несложно — это полупроизведение катетов (сторон, между которыми лежит прямой угол). Таким образом, даже если стороны двух фигур по длине разные, но их произведение равно, они равновеликие. Например, треугольник с катетами 4 и 4 равен по площади многоугольнику с катетами 16 и 1. Так как их полупроизведение, а значит и площадь равна 8.
Если же треугольник произвольный (то есть не является частным случаем — прямоугольным, равнобедренным или равносторонним), можно воспользоваться одной из 5 формул, позволяющих вычислить его площадь.
То, какую формулу использовать, будет зависеть от данных, предоставленных в задаче. Иногда придётся проводить дополнительное построение, например, провести высоту или использовать свойства, что биссектрисы пересекаются в центре вписанной окружности. Если не даны все 3 стороны, использовать третью формулу не получится.
Важно понять, что фигуры могут быть разными по количеству углов, но всё равно считаться равновеликими — в учёт идёт только площадь, остальные параметры не важны. Например, прямоугольный треугольник с катетами 2 и 4 будет визуально казаться больше, чем квадрат со стороной 2, но их площади совпадают и равны 4 (площадь прямоугольника считается как произведение прилежащих сторон друг на друга). По определению это делает их равновеликими.
Визуальный способ
Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.
Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.
Равновеликие фигуры
Равновеликие фигуры — это фигуры, которые имеют одинаковые площади.
Равновеликие тела — это тела, которые имеют равные объёмы (равновеликие тела часто также называют равновеликими фигурами). Равные фигуры — это фигуры, которые совпадают при наложении (у них соответствующие стороны равны и соответствующие углы равны).
Равные фигуры имеют равные площади, поэтому равные фигуры являются также равновеликими. Обратное, вообще говоря, неверно.
1) Прямоугольник и квадрат, изображенные на рисунке 1, — равновеликие фигуры.
То есть, прямоугольник со сторонами a и b и квадрат со стороной c являются равновеликими, если
2) Треугольник и квадрат, изображенные на рисунке 2 — равновеликие фигуры, так как имеют равные площади.
Площадь квадрата S=3²=9.
Треугольник со стороной a и проведенной к ней высоте ha и квадрат со стороной c являются равновеликими, если
3) Треугольник и трапеция, изображенные на рисунке 3 — равновеликие, поскольку их площади равны.
Треугольник со стороной c и проведенной к ней высотой hс и трапеция с основаниями a и b и высотой h являются равновеликими, если
Подобие фигур
Подобие фигур — это две геометрические фигуры или два геометрических тела называются подобными, если одно представляет собой уменьшенную модель другого.
Содержание:
Понятие подобия фигур
В окружающем мире часто встречаются предметы, одинаковые по форме, но различные по размерам: мыльный пузырь и футбольный мяч, небольшая модель ледокола и сам корабль, карты, фотоснимки различных размеров одного и того же здания. В геометрии такие фигуры называют подобными.
Существуют фигуры, которые всегда подобны друг другу, например, круги, квадраты, кубы.
Для обозначения подобия фигур употребляется знак 
. На рисунке 2.434 изображены подобные фигуры 
. Запись 
читается: фигура 
подобна фигуре 
Для подобных фигур вводится понятие — коэффициент подобия, он обозначается k; k всегда больше нуля. Коэффициент подобия показывает, в каком отношении находятся соответствующие расстояния между точками фигур. На рисунке 2.434 коэффициент подобия можно определить, найдя отношения сторон квадратиков изображенной сетки.
Подобие фигур широко используется при разработке планов построек зданий или при изображении на картах городов или других участков земной поверхности. Всякий план или карта является подобным изображением реального объекта или участка земной поверхности, т. е. фигурой, подобной реальному объекту. При этом план или карта может изображать реальный объект в разном масштабе.
Определение. Масштаб — это коэффициент подобия соответствующих фигур.
Подобие треугольников
На рисунке 2.435 изображены два чертежных прямоугольных треугольника с острыми углами в 60° и 30°. Стороны второго треугольника по сравнению с первым уменьшены в два раза: 
У этих треугольников углы попарно равны. Стороны, лежащие против разных углов, пропорциональны: 
Такие треугольники называют подобными. Стороны, лежащие против равных углов, называют сходственными.
Определение. Подобными называют треугольники, у которых углы попарно равны, а сходственные стороны пропорциональны.
Подобие треугольников записывается так: 
Отношение сходственных сторон подобных треугольников называется коэффициентом подобия. В случае, изображенном на рисунке 2.435, коэффициентом подобия треугольников 
будет число 2. Если же взять отношения 
, коэффициент подобия будет равен 
.
Подобные треугольники могут быть произвольно расположены как на плоскости, так и в пространстве.
Если фигуры равны, то они подобны с коэффициентом подобия, равным 1. Если фигуры подобны, то они не обязательно равны.
Теорема 1. (Лемма о подобии треугольников). Прямая, пересекающая две стороны треугольника и проведенная параллельно третьей стороне, отсекает треугольник, подобный данному.
Для выявления подобия треугольников существуют признаки подобия треугольников.
Теорема 2. (Первый признак — по двум равным углам.) Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.
Следствия из этой теоремы.
1. Равносторонние треугольники подобны.
2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.
3. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.
4. Равнобедренные прямоугольные треугольники подобны.
Теорема 3. (Второй признак — по пропорциональности двух сторон и равенству углов между ними.) Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.
Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.
Теорема 4. (Третий признак — по пропорциональности трех сторон.) Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Подобие многоугольников
Определение. Если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы этих многоугольников равны, то такие многоугольники подобны.
Для многоугольников с числом сторон больше трех признак подобия, аналогичный третьему признаку подобия треугольников, будет неверен. Например, квадрат и ромб, отличный от квадрата, не будут подобны, хотя их стороны пропорциональны (рис. 2.437). Недостаточно для подобия двух прямоугольников и равенства их соответствующих углов. Например, квадрат не подобен четырехугольнику, не все стороны которого равны (рис. 2.438).
Теорема 6. Отношение периметров подобных многоугольников равно отношению их сходственных сторон (коэффициенту подобия).
Теорема 7. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»: