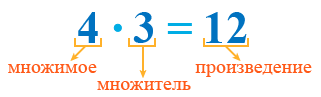Что такое одинаковый множитель

Вынесение общего множителя за скобки

5 класс, 6 класс, 7 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие вынесения множителя за скобки

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

Есть несколько способов разложения многочлена на множители. Один из них — вынесение общего множителя за скобки.

Вынести общий множитель за скобки можно в выражениях, которые представляют из себя суммы, в которых каждое слагаемое является произведением, причем в каждом произведении есть один одинаковый для всех множитель. Он так и называется — общий множитель.

Вынесение общего множителя за скобки — это преобразование многочлена в произведение с помощью распределительного свойства умножения. Только в случае вынесения множителя за скобки это свойство применяется справа налево.

Формула вынесения общего множителя за скобки:

Покажем метод вынесения общего множителя за скобки на примере с цифрами:

Определение общего множителя для всех членов многочлена производится пошагово:

Если нам дано произведение 6 * 2 и 6 * 5, то мы можем вынести за скобки общий множитель 5. В чем состоит данное преобразование? Мы представляем исходное выражение как произведение общего множителя и выражения в скобках, которое содержит сумму всех исходных слагаемых, кроме общего множителя.

Итак, вынесем общий множитель 5 в 6 * 2 и 6 * 5 и получим 6 * (2 + 5).

Итоговое выражение — это произведение общего множителя 6 на выражение в скобках, которое является суммой исходных слагаемых без 6.

Так и получается: 6 * 2 + 6 * 5 = 6 * (2 + 5).

Правило вынесения общего множителя за скобки

Основное правило вынесения общего множителя за скобки

Чтобы вынести за скобки общий множитель, нужно записать исходное выражение в виде произведения общего множителя и скобок, которые включают в себя исходную сумму без общего множителя.

Алгоритм вынесения общего множителя за скобки:

Важно! В скобках должно быть столько одночленов, сколько их было в многочлене.

Это и есть итог нашего преобразования. Запись всего решения выглядит так:

Определить сразу, какой множитель является общим, получается не всегда. Иногда выражение нужно предварительно преобразовать, заменив числа и выражения тождественно равными им произведениями.

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Вынесение минуса за скобки

Еще один случай, на котором следует обратить внимание — это вынесение за скобки минуса. Только мы выносим не сам знак, а минус единицу. Часто это помогает упростить выражение и сделать его проще.

Чтобы вынести минус за скобки, нужно записать перед скобками минус и в скобках записать все слагаемые с противоположными знаками:

Найдем решение для каждого выражения:

Поэтому между выражениями можно поставить знак равенства, потому что они равны одному и тому же значению:

Ставим минус и рядом в скобках записываем выражение с противоположным знаком у каждого слагаемого:

Как и в прошлом примере, здесь за скобки вынесен не минус, а минус единица.

Источник

Что такое множитель и разложение на простые множители

Дадим определение понятию «множитель» и разберемся что такое множитель. Какие множители бывают и почему некоторые из множителей — простые.

Определение множителя

В младших классах вы учили, что множители — это числа, которые мы умножаем, называя результат их умножения произведением.

Определения множителя как компонента умножения

Сейчас немного расширим понятие множителя.

Давайте рассмотрим определение множителя на примерах. Давайте определим где в представлении числа или выражения прячется множитель?

Пример 1

Пусть нам дано число 15. Это число можно представить в виде произведения . Значит, согласно определению 5 — это множитель, 3 — это тоже множитель.

Пример 2

Рассмотрим теперь выражение: . Это выражение можно представить в виде произведения . Получаем два множителя — первый множитель (2x-3) и второй множитель (2x+3).

Самое простое произведение имеет два множителя, но может быть и больше множителей.

Простые множители

Пример 1

Разложите число 65 на простые множители.

Решение: число 65 будем делить на простые числа, пока оно нацело не разделится. Так мы видим, что число 65 не делится на 2, 3 и 4, так как не соответствует признакам делимости на эти числа. Зато делится на 5, так как оканчивается на 5. При делении мы получаем 13. Число 13 — простое, так как делится только на себя и на единицу. Таким образом, число . И мы выполнили разложение числа на простые множители. Теперь вы знаете, как разложить число на простые множители.

Пример 2

Разложите число 270 на простые множители.

Решение: Разделим сначала число 270 на 2 (сначала берем самое маленькое простое число), получим 135. Посмотрим, делится ли это число на 3. Для этого сложим все числа, стоящие в разрядах данного числа — . Девять делится на 3, значит, и число 135 разделится на 3: . Получившееся число опять делится на 3: . И снова число 15 делится на 3: . Получили простое число 5. Делим .

Итак, запишем разложение числа 270 на простые множители в виде столбца, где справа от черты мы пишем на какое простое число мы делим, а слева — что получаем:

Разложение числа на простые множители в столбик.

Разложение числа на простые множители в строчку записывается так: .

Про разложение многочлена на множители поговорим в отдельной теме.

Источник

Вынесение за скобки общего множителя: правило, примеры

В рамках изучений тождественных преобразований очень важна тема вынесения общего множителя за скобки. В данной статье мы поясним, в чем именно заключается такое преобразование, выведем основное правило и разберем характерные примеры задач.

Понятие вынесения множителя за скобки

Чтобы успешно применять данное преобразование, нужно знать, для каких выражений оно используется и какой результат надо получить в итоге. Поясним эти моменты.

В чем состоит данное преобразование? В ходе него мы представляем исходное выражение как произведение общего множителя и выражения в скобках, содержащего сумму всех исходных слагаемых, кроме общего множителя.

Правило вынесения общего множителя за скобки

Используя все сказанное выше, выведем основное правило такого преобразования:

Чтобы вынести за скобки общий множитель, надо записать исходное выражение в виде произведения общего множителя и скобок, которые включают в себя исходную сумму без общего множителя.

Определить сразу, какой множитель является общим, возможно не всегда. Иногда выражение нужно предварительно преобразовать, заменив числа и выражения тождественно равными им произведениями.

В выводах отметим, что преобразование путем вынесения общего множителя за скобки очень часто применяется на практике, например, для вычисления значения рациональных выражений. Также этот способ полезен, когда нужно представить выражение в виде произведения, например, разложить многочлен на отдельные множители.

Источник

Разложение на множители что значит и как раскладывать на простые множители число, корни, трехчлен, квадратное уравнение, примеры и решения, правило и алгоритм

При решении математических уравнений часто приходится преобразовывать равенства для упрощения выражений. Делается это с помощью разложения на множители. Приводить к простому виду можно как многочлены, так и одночлены, при этом необязательно знать даже формулы. Для решения сложных заданий можно воспользоваться онлайн-калькулятором. Пользоваться им несложно, главное, иметь чёткое условие задачи и доступ к интернету.

Термины и понятия

Под разложением в математике понимается операция, которую выполняют для превращения сложного неудобного для вычисления примера в простой. В учебниках и литературе такое преобразование выражений называется тождественным, то есть без изменения сути задания.

Из слова «множители» можно понять, что в превращении используется умножение. Зная, как разложить полином на простые числа, можно быстро решать задачи на действия с корнями и сложными дробями. Например, выражение (3*h*y + 9*y — 8*h — 24) * (3*h — 8) после упрощения примет вид: h + 3 — и быстро решается в уме.

В математике все алгебраические выражения могут быть:

Числа часто записывают в так называемом стандартном виде. Например, 296,8 = 2,968 * 102. То есть используется формула приведения: a * 10r, где 1≤а Простое разложение

На уроках математики ученикам предлагают разложить на простые множители числа с помощью столбика (двух колонок). Делается это по следующему алгоритму. Исходное число проверяют на возможность деления без остатка на два. Если делится, то рисуют две колонки, в правую вписывают двойку, а в левую число, получившееся после деления на него исходного. В обратном случае вместо двойки используют цифру три. Далее действия повторяют для числа, находящегося уже в правой колонке. Выполняют деление до тех пор, пока в левой колонке не останется единица. Например, число 1176 можно разложить следующим образом:

1176 | 2 (1176 / 2 = 588).

588 | 2 (588 / 2 = 294).

294 | 2 (294 / 2 = 147).

1176 = 2 * 2 * 2 * 3 * 7 * 7 = 23 * 3 * 72.

Для того чтобы понять алгоритм, лучше рассмотреть ещё несколько интересных примеров:

Используя метод, можно представить любое число как произведение простых множителей, но с условием, что изначально оно будет кратным двум или трём. В ином же случае простые множители подобрать не получится, как, например, для числа 247, которое можно заменить произведением чисел 13 и 19.

Вынесение коэффициента

Это довольно простой способ разложения многочлена. Выполняют его с помощью перестановки общего множителя за скобку, в которой остаётся сумма выражения. То есть для этого метода необходимо представить искомое в виде произведения нескольких полиномов.

Чтобы выделить общий множитель, следует выполнить:

Например, пусть дано выражение: 3у2 — 3y + 6 r*y. Согласно правилу, необходимо найти число, на которое без остатка можно разделить каждый из трёх коэффициентов многочлена. Для рассматриваемого примера это будет цифра 3.

Затем определить буквенный множитель, имеющийся в каждом члене выражения. Найденную цифру и повторяющееся неизвестное с наименьшей степенью записать за скобкой. Теперь нужно каждый одночлен разделить на вынесенное значение, а полученный результат записать в скобках: 3y * (y — 1 + 2r). Для проверки правильности действий нужно просто раскрыть скобки путём умножения каждого члена на вынесенный множитель.

Формулы умножения

Довольно часто для упрощения расчётов используют формулы сокращённого умножения. Всего существует семь выражений, которые необходимо выучить. Найти их можно в таблицах любого учебника по алгебре за седьмой класс. Смысл этих теорем в следующем:

Все эти формулы умножения можно использовать также в обратную сторону, то есть собирать многочлен. Например, для решения примеров типа: «квадратный трёхчлен разложен на множители, найдите а». Если понять смысл этих формул, то запомнить их наизусть будет довольно легко.

Метод группировки

Пожалуй, самый распространённый способ разложения на множители. Его удобно применять для упрощения квадратных уравнений без поиска корней. Разложение этим методом выполняют в следующей последовательности действий:

Выполнять группировку можно по-разному, но в итоге обязательно должен остаться общий многочлен. Например, выражение 48 * h * e 2 + 32 * h * q — 15 * e 2 — 10 * q2 возможно решить двумя способами.

Для того чтобы вынести многочлен за скобку, может понадобиться инвертировать все знаки. Следует помнить, что при выносе минуса у всех одночленов, оставшихся под скобкой, знак изменится на противоположный.

Выделение квадрата

По сути, выделение общего квадрата соответствует преобразованию, при котором трёхчлен представляют в виде (k + e)2 или (k — e)2. Метод используется для решения биквадратных уравнений. Для выделения полного квадрата при разложении многочлена на множители применяют две формулы:

Например, нужно упростить дробь: (k4 + 4 * e4) / (k4 + 2 * e2 + 2 * k * e). Необходимо разложить числитель, используя формулы для полного квадрата: (k4 + 4 * e4) = (k4 + 4 * e2 * k2 + 4 * e 4). Значит, если отнять от многочлена 4 * k2 * e2, то получится уравнение: (k2 + 2 * e2) * 2 − 4 * k2 * e2. Используя формулу умножения квадратов, верно будет записать: (k2 + 2 e 2 − 2 * k * e) * (k2 + 2 e 2 + 2 * k * e).

Заменив полученным выражением числитель, можно будет его часть взаимно сократить со знаменателем. В итоге получится простое выражение: h2 + 2 * e2 − 2 * h * e.

Неприводимые множители

Решая различные задачи, можно столкнуться со сложными выражениями, которые, как кажется, разложить нельзя. Например, (2 * p2 — 5 * p — 3)/(3 * p — 9). В числителе дроби находится квадратный трёхчлен, который на самом деле можно разложить. Для того чтобы его можно было упростить, используется формула: ar2 + br + p = a (r — r1) * (r — r2), где r1 и r2 корни выражения.

Чтобы найти решения для линейного уравнения, необходимо определить дискриминант. То есть нужно из задачи отделить числитель, найти его решения и подставить найденные значения в формулу разложения.

Теперь вместо числителя нужно подставить полученное разложение: (2*p2 — 5*p — 3)/(3*p — 9) = 2*(p — 3) * (p + ½)/3 * (p — 3) = (2 *p + 1)/3.

Использование онлайн-калькуляторов

Порой, для решения сложных заданий нужно затратить много времени. При этом всегда существует риск допустить ошибку при расчётах. Чтобы этого избежать или проверить свой ответ, можно воспользоваться сайтами, предлагающие онлайн-калькуляторы. Использовать их сможет даже пользователь, совершенно не понимающий методов, используемых для упрощения выражений.

Расчёт обычно занимает менее 30 секунд. Приложений для упрощений уравнений достаточно много. Написаны они на Паскале или javascript. Появление ошибки при вычислении невозможно. Нередко на этих сайтах ещё и содержится информация о способах упрощения полиномов.

Для того чтобы получить ответ, необходимо будет с помощью браузера зайти на сайт онлайн-калькулятора и заполнить предлагаемые им поля. После того как упрощаемое выражение будет вписано, следует нажать кнопку «Рассчитать» или «Упростить выражение» и получить ответ с пошаговым решением.

Источник

Умножение натуральных чисел

Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.

Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе?

Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4.

Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах.

Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.

Для записи умножения используется знак х (косой крест) или · (точка), который ставится между числами. Например:

Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак = (равно), после которого записывается полученный результат:

Умножение – это краткая запись сложения одинаковых слагаемых.

Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:

Сократим запись, заменив сложение на умножение:

Оба выражения равны:

6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,

но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.

Множимое, множитель и произведение

Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:

4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.

Произведение — это число, которое получается в результате умножения. Например, в записи:

12 — это произведение. При этом сама запись 4 · 3 тоже называется произведением.

Множимое и множитель иначе называются множителями или сомножителями.

Проверка умножения

Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.

Источник