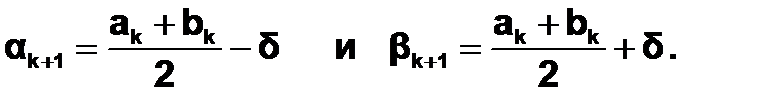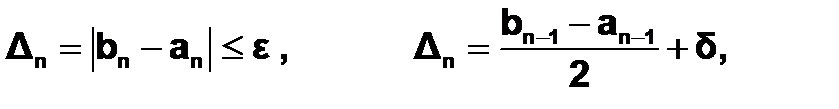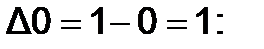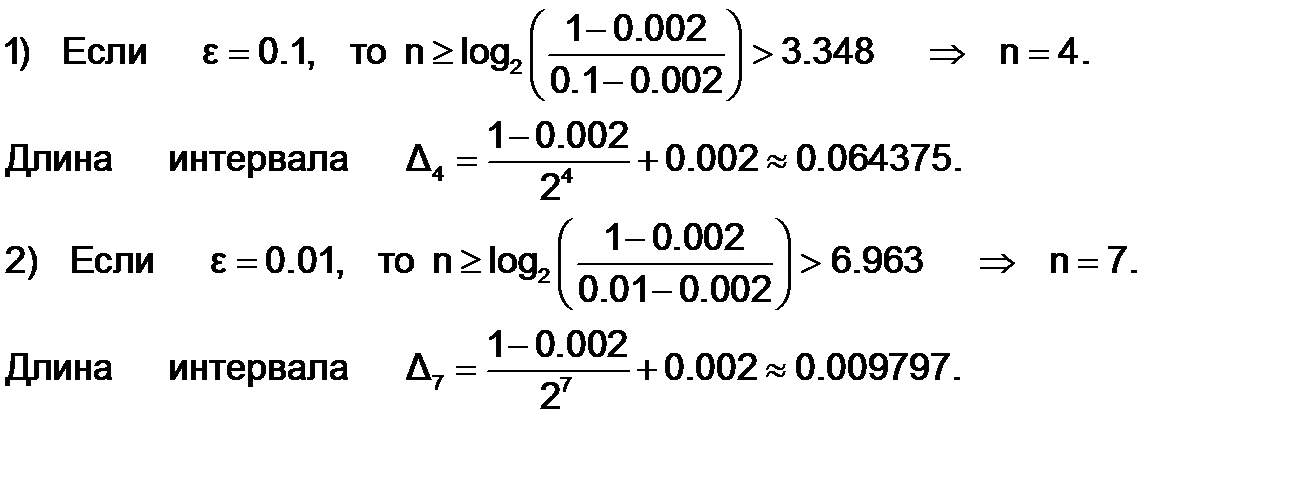Что такое одномерная оптимизация

Одномерная оптимизация

Задача оптимизации – одна из важнейших составляющих многих инженерных задач. Найти оптимальное решение – означает найти наилучший, в смысле заданного критерия, вариант из всех возможных. При решении задачи оптимизации рассматривается некоторая функция, называемая целевой(иликритериальной), и аргументы (параметры целевой функции), называемые параметрами оптимизации.

По количеству независимых переменных различают задачи одномерной оптимизации (n=1) и многомерной оптимизации (n³ 2). При этом задача нахождения максимума целевой функции сводится к задаче нахождения минимума путем замены функции f(x) на -f(x), поэтому в дальнейшем будем говорить только о поиске минимума функции, то есть такого x*Î[a, b], при котором f(x*) = minf(x).

Проверим достаточное условие существования минимума на выбранных отрезках:

f¢(0) 0, f¢¢ (x) > 0 для хÎ[0;1],

f¢(-4) 0, f¢¢ (x) > 0 для хÎ[-4;-3].

Условия существования минимума выполнены, поскольку f¢¢(x) > 0 для всех хÎ[0;1] и хÎ[-4;-3]. Следовательно, функция f(x) является унимодальной на выбранных отрезках.

На практике численные методы одномерной оптимизации применяют в следующих случаях:

· значения функции f(x) определены в ходе эксперимента;

· целевая функция очень сложна или не имеет непрерывных производных;

· классические методы поиска оптимального значения не применимы.

Суть методоводномерного поисказаключается в том, что на каждой итерации интервал неопределенности уменьшается и стягивается к точке минимума. Уменьшение отрезка происходит до тех пор, пока на некоторой n-й итерации отрезок неопределенности[b_n;a_n] нестанет соизмеримым с заданной погрешностьюe, то естьбудет выполняться условие|b_n-a_n| f(b₁),тоx*Î[a₁;b₀] (Рис. 1.6.1-3.b).

Если описанную процедуру принять за одну итерацию, то алгоритм поиска минимума можно описать следующим образом. Опишем k+1 итерацию, исходя из того, что k-й отрезок неопределенности найден [a_k;b_k]:

1.Вычисляются

2.Находят значения f(a_k₊₁) и f(b_k₊₁).

3.Находят k+1-й отрезок неопределенности по правилу:

Вычисления проводятся до тех пор, пока не выполнится неравенство

где D_n– длина n-го отрезка неопределенности.

Выберем d =0.001 и положим a = 0;b = 1;

n	a	b	a₁	b₁	f(a₁)	f(b₁)	D_n
0.499	0.501	0.23239	0.23067	0.501
0.499	0.7485	0.7505	0.14392	0.14435	0.2515
0.499	0.7505	0.62375	0.6257	0.15486	0.15413	0.12675
0.62375	0.7505	0.68613	0.6881	0.14040	0.14023	0.06437
…	…..	…..	…..	….	…..	…..	….
0.701719	0.71931	0.70951	0.7115	0.13954	0.13959	0.00979

Приe = 0.1 x*=0.7183 f(x*)=0.1399, а при e = 0.01 x*=0.7066 f(x*)=0.13951
.

Дата добавления: 2016-05-31 ; просмотров: 4581 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник