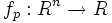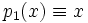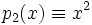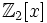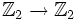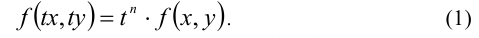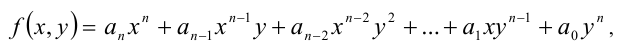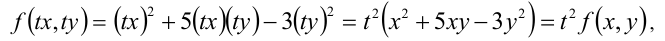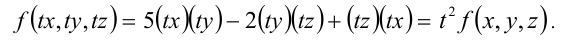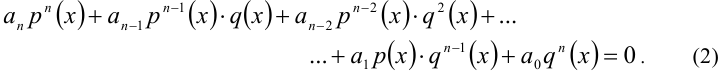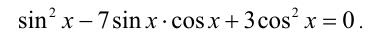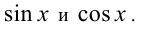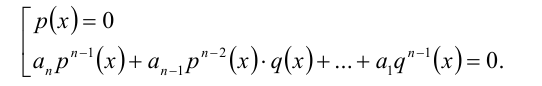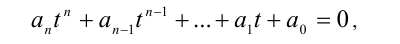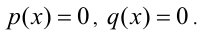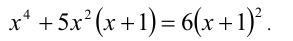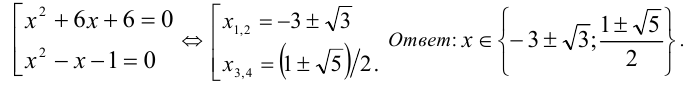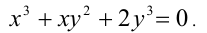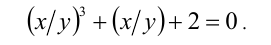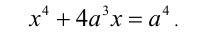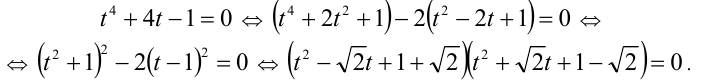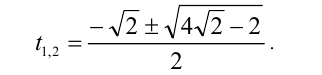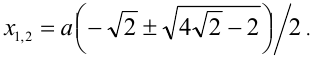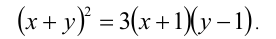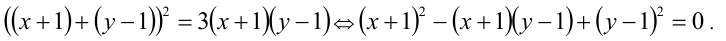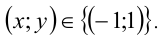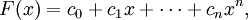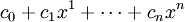Что такое однородный многочлен

Однородный многочлен

Одноро́дный многочле́н — многочлен, все одночлены которого имеют одинаковую полную степень. Любая алгебраическая форма является однородным многочленом.

Примеры

Вариации и обобщения

См. также

Полезное

Смотреть что такое «Однородный многочлен» в других словарях:

ОДНОРОДНЫЙ МНОГОЧЛЕН — многочлен, у всех членов которого сумма показателей степеней входящих в него переменных (неизвестных) одинакова. Напр.: x5+4x3y2 3xy4 … Большой Энциклопедический словарь

однородный многочлен — многочлен, у всех членов которого сумма показателей степеней входящих в него переменных (неизвестных) одинакова. Например: х5+4х3у2 3ху4. * * * ОДНОРОДНЫЙ МНОГОЧЛЕН ОДНОРОДНЫЙ МНОГОЧЛЕН, многочлен, у всех членов которого сумма показателей… … Энциклопедический словарь

ОДНОРОДНЫЙ МНОГОЧЛЕН — многочлен, у всех членов к рого сумма показателей степеней входящих в него переменных (неизвестных) одинакова. Напр.: х5+ 4х3у2 3ху4 … Естествознание. Энциклопедический словарь

Многочлен Лорана — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Общий метод решета числового поля — (англ. general number field sieve, GNFS) метод факторизации натуральных чисел. Является наиболее эффективным алгоритмом факторизации чисел длиной более 110 десятичных знаков. Сложность алгоритма оценивается эвристической формулой[1] Метод… … Википедия

Двучлен — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Моном — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Полином — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Источник

ОДНОРОДНЫЙ МНОГОЧЛЕН

Смотреть что такое «ОДНОРОДНЫЙ МНОГОЧЛЕН» в других словарях:

Однородный многочлен — многочлен, все одночлены которого имеют одинаковую полную степень. Любая алгебраическая форма является однородным многочленом. Примеры однородный многочлен однородный многочлен однородный многочлен неоднородный многочлен … Википедия

однородный многочлен — многочлен, у всех членов которого сумма показателей степеней входящих в него переменных (неизвестных) одинакова. Например: х5+4х3у2 3ху4. * * * ОДНОРОДНЫЙ МНОГОЧЛЕН ОДНОРОДНЫЙ МНОГОЧЛЕН, многочлен, у всех членов которого сумма показателей… … Энциклопедический словарь

ОДНОРОДНЫЙ МНОГОЧЛЕН — многочлен, у всех членов к рого сумма показателей степеней входящих в него переменных (неизвестных) одинакова. Напр.: х5+ 4х3у2 3ху4 … Естествознание. Энциклопедический словарь

Многочлен Лорана — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Общий метод решета числового поля — (англ. general number field sieve, GNFS) метод факторизации натуральных чисел. Является наиболее эффективным алгоритмом факторизации чисел длиной более 110 десятичных знаков. Сложность алгоритма оценивается эвристической формулой[1] Метод… … Википедия

Двучлен — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Моном — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Полином — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Источник

Однородные уравнения

Однородные уравнения

Это означает, что однородный многочлен n-й степени f (х, у) можно представить в виде

где 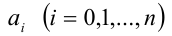— коэффициенты многочлена, одновременно не обращающиеся в нуль.

т.е. условие (1) из определения выполняется (n = 2).

Итак, однородное алгебраическое уравнение — это уравнение, не меняющее своего вида при одновременном умножении всех его неизвестных на одно и то же число, отличное от нуля. Можно распространить понятие однородности на случай неалгебраических уравнений.

Пусть р(х) и q(x) — две произвольные функции, определённые на одном и том же множестве, .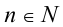

В частности, если функции р(х) и q(x) являются целыми алгебраическими многочленами, то и уравнение (2) будет относиться к аналогичному классу. В качестве другого примера рассмотрим уравнение вида

Оно является однородным тригонометрическим уравнением 2-й степени относительно функций

Перейдём к процедуре решения уравнения (2).

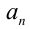
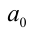
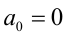
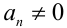
Если хотя бы один из коэффициентов или обращается в нуль, то левая часть уравнения легко раскладывается на множители. В результате уравнение оказывается равносильно на ОДЗ совокупности двух уравнений. Например, если , то получим совокупность

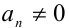
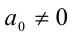
Если же и , то для решения однородного уравнения (2) необходимо рассмотреть два возможных случая.

решив которое и сделав обратную подстановку, найдём часть решений однородного уравнения.

2) Если q(х) = 0. то, подставив в уравнение вместо q(x) нуль, получим, что тогда и р(х) должно обращаться в нуль. Таким образом, этот случай сводится к решению системы уравнений

Осталось объединить все найденные решения. Уравнение (2) решено. Обратимся к примерам.

Пример №185.

Решить уравнение

Решение:

Пример №186.

Решить в целых числах уравнение

Решение:

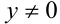
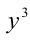
Заметим, что если у = 0, то x = 0, и, значит, пара (0;0) удовлетворяет уравнению. Пусть , тогда поделим обе части уравнения на :

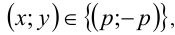
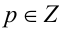
Ответ: где .

Пример №187.

Для каждого действительного значения параметра а решить уравнение

Решение:

Заметим, что данное уравнение можно рассмотреть как однородное алгебраическое уравнение 4-й степени относительно x и а.

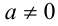
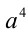
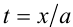
2) Если , то поделим на , и положим :

Первый сомножитель в нуль не обращается, а второй имеет два корня

Ответ: при а = 0 единственное решение x = 0 ;

при 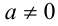два решения

Пример №188.

Найти действительные корни уравнения

Решение:

Данное уравнение в исходном виде не является однородным, но может быть сведено преобразованиями к однородному. Действительно, достаточно привести его к виду

Получили однородное уравнение 2-й степени относительно x + 1 и у — 1.

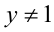
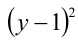
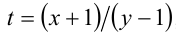
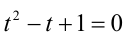
1) Если , то, поделив на и обозначив , получим нет решений.

Ответ:

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Однородная функция

СОДЕРЖАНИЕ

Примеры [ править ]

Пример 1 [ править ]

Например, предположим, что x = 2, y = 4 и t = 5. Тогда

Линейные функции [ править ]

Любое линейное отображение ƒ : V → W однородно степени 1, поскольку по определению линейности

Аналогично, любая полилинейная функция ƒ : V ₁ × V ₂ × ⋯ × V _n → W однородна степени n, поскольку по определению полилинейности

Однородные многочлены [ править ]

однородна степени 10, так как

Однородный многочлен является многочленом из суммы одночленов той же степени. Например,

x 5 + 2 x 3 y 2 + 9 x y 4 <\displaystyle x^<5>+2x^<3>y^<2>+9xy^<4>\,>

является однородным многочленом степени 5. Однородные многочлены также определяют однородные функции.

( x k + y k + z k ) 1 k <\displaystyle \left(x^+y^+z^\right)^<\frac <1>>>

Мин. / Макс. [ Редактировать ]

Поляризация [ править ]

Рациональные функции [ править ]

Не примеры [ править ]

Логарифмы [ править ]

Аффинные функции [ править ]

Положительная однородность [ править ]

В частном случае векторных пространств над действительными числами понятие положительной однородности часто играет более важную роль, чем однородность в указанном выше смысле.

Все приведенные выше определения можно обобщить, заменив равенство f ( rx ) = r f ( x ) на f ( rx ) = | г | f ( x ), и в этом случае мы ставим перед этим определением слово « абсолютный » или « абсолютно ». Например,

Обобщения [ править ]

Моноиды и моноидные действия [ править ]

Однородность [ править ]

Если мы говорим, что функция однородна над M (соответственно, абсолютно однородна над M ), мы имеем в виду, что она однородна степени 1 над M (соответственно абсолютно однородна степени 1 над M ).

Понятие бытия абсолютно однородна степени к над М обобщена аналогично.

Теорема Эйлера об однородных функциях [ править ]

Непрерывно дифференцируемые положительно однородные функции характеризуются следующей теоремой:

Теорема может быть специализирована для случая функции одной действительной переменной ( n = 1 ), и в этом случае функция удовлетворяет обыкновенному дифференциальному уравнению

f ′ ( x ) − k x f ( x ) = 0. <\displaystyle f'(x)-<\frac >f(x)=0.>

Однородные распределения [ править ]

t − n ∫ R n f ( y ) φ ( y t ) d y = t k ∫ R n f ( y ) φ ( y ) d y <\displaystyle t^<-n>\int _ <\mathbb ^>f(y)\varphi \left(<\frac >\right)\,dy=t^\int _ <\mathbb ^>f(y)\varphi (y)\,dy>

Приложение к дифференциальным уравнениям [ править ]

Подстановка v = y / x преобразует обыкновенное дифференциальное уравнение

Источник

Полиномы

где c_i фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций.

Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.

Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (смотри аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе.

Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования, или выражения многочленами свойств различных объектов.

Содержание

Определение

Многочлен (или полином) от n переменных — есть конечная формальная сумма вида

,

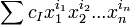
где I = (i₁,i₂. i_n) есть набор из целых неотрицательных чисел (называется мультииндекс), c_I — число (называемое «коэффициент многочлена»), зависящее только от мультииндекса I.

В частности, многочлен от одной переменной есть конечная формальная сумма вида

Коэффициенты многочлена обычно берутся из определённого коммутативного кольца R (чаще всего поля, например, поля вещественных или комплексных чисел). В этом случае, относительно операций сложения и умножения многочлены образуют кольцо (более того ассоциативно-коммутативную алгебру над кольцом R без делителей нуля) которое обозначается

Связанные определения

Делимость

Например, многочлен x 4 + 2, неприводимый в поле рациональных чисел, разлагается на два множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.

Вообще, каждый многочлен от одного переменного x разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).

Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого n > 2 существуют многочлен от n переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми.

Полиномиальные функции

.

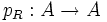
В случае если R есть поле вещественных или комплексных чисел (а также любое другое поле с бесконечным числом элементов) то функция полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены и из определяют тождественно равные функции .

Источник