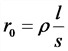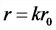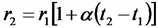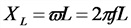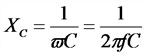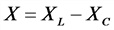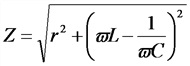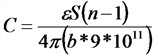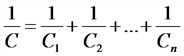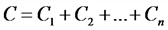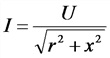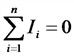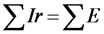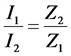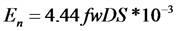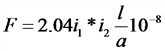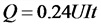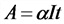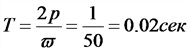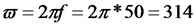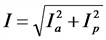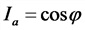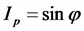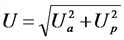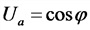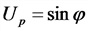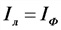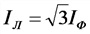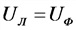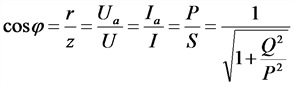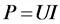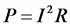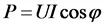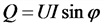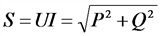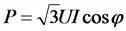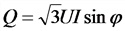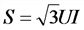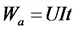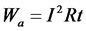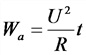Что такое омега в электротехнике
Переменный (синусоидальный) ток и основные характеризующие его величины.
Переменный ток (англ. alternating current — AC) — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.
В быту для электроснабжения переменяется переменный, синусоидальный ток.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рисунок 1):
Максимальное значение функции называют амплитудой. Её обозначают с помощью заглавной (большой) буквы и строчной буквы m — максимальное значение. К примеру:
Период Т— это время, за которое совершается одно полное колебание.
f = 1/T
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси)
В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j (или e(t) и j(t)).
Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 10 3 Гц = 1 кГц;
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2
Рисунок 2. Радиан.
1рад = 360°/2
? = 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Основные формулы электротехники.
В таблице представлены основные расчетные формулы по электротехнике для расчета тока, напряжения, сопротивления, мощности и других парметров электрических схем.
Измеряемые величины
Формулы
Обозначение и единицы измерения
Сопротивление проводника омическое (при постоянном токе)
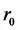
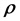
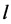
Активное сопротивление при переменном токе
r — активное сопротивление, Ом;
k — коэффициент, учитывающий поверхностный эффект, а в магнитных проводниках — также явление намагничивания
Зависимость омического сопротивления проводника от температуры
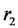
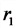
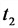
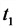
Индуктивное (реактивное) сопротивление
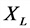
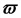
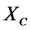
L — коэффициент самоиндукции (индуктивность), Гц;
Z — полное сопротивление, Ом
Емкостное (реактивное) сопротивление
Полное реактивное сопротивление
Полное сопротивление переменному току
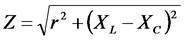
Емкость пластинчатого конденсатора
S — площадь между двумя
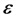
b — толщина слоя диэлектрика, см
Общая емкость цепи:
а) при последовательном соединении емкостей
б) при параллельном соединении емкостей
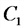
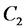
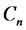
Закон Ома; цепь переменного тока с реактивным сопротивлением
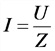
U — напряжение цепи, В;
1-й закон Кирхгофа (для узла)

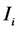
Е — ЭДС, действующая в контуре, В;
r — сопротивление отдельных
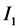
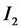
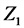
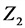
2-й закон Кирхгофа (для замкнутого контура)
Распределение тока в двух параллельных ветвях цепи переменного тока
Закон электромагнитного индукции для синусоидального тока
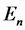
w — число витков обмотки;
В — индукция магнитного поля в стали, Тс;
S — сечение магнитопровода, см2
Электродинамический эффект тока для двух параллельных проводников
F — сила, действующая на 1 (см) длины проводника, кГ;
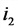
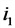
а — расстояние между проводниками, си;
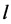
Подъемная сила электромагнита
Р — подъемная сила, кГ;
В3 — индукция в воздушном
зазоре; В3 = 1000 Гс (электромагниты для подъема стружки и мелких деталей); В3 = 8000 — 10 000 Гс (электромагниты для подъема крупных деталей)
S — сечение стального сердечника, см2
Тепловой эффект тока
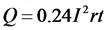
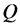
t— время протекания тока, сек;
r — сопротивление, Ом;
А — количество вещества, от-
ложившегося на электроде, мг;
α — электрохимический эквивалент вещества
Химический эффект тока
Зависимости в цепи переменного тока при частоте 50 Гц:
а) период изменения тока
б) угловая скорость
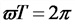
Т — период изменения тока, сек;
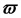
Зависимости токов и напряжений в цепи переменного тока:
б) напряжение в цепи
I — полный ток в цепи, А;
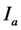
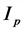
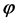
U— напряжение в цепи, В;

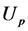
Соотношения токов и напряжений в трехфазной системе:
а) соединение в звезду
б) соединение в треугольник
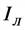
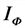
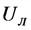
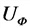
Р — активная мощность, Вт;
Q — реактивная мощность, нар;
S —полная мощность, B*А;
r — активное сопротивление,
Мощность в цепи постоянного тока
Мощность в цепи переменного тока:
а) цепь однофазно тока
б) цепь трехфазного тока
Энергия в цепи постоянного тока
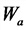
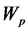
Чему равна омега в физике
| Угловая частота | |
|---|---|
| ω | |
| Размерность | T −1 |
| Единицы измерения | |
| СИ | рад/с |
| СГС | рад/с |
| Другие единицы | градус/с |
Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).
Угловая частота является производной по времени от фазы колебания:
Угловая частота связана с частотой ν соотношением [1]
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2 π единиц времени.
В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2 π и 1/(2 π ), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.
| В Викисловаре есть статья « омега » |
Омега (греч. ὦ μέγα — большое «о») — последняя буква греческого алфавита. А также:
Содержание
Омега в математике и информатике [ править | править код ]
Омега в химии и физике [ править | править код ]
Омега в астрономии [ править | править код ]
Топонимы [ править | править код ]
Подразделения специального назначения [ править | править код ]
Музыкальные группы и произведения [ править | править код ]
Автомашины [ править | править код ]
«Омега» как марка технических устройств [ править | править код ]
«Омега» в художественных произведениях, кинематографии и компьютерных играх [ править | править код ]
•Омега-персонаж из fortnite
Рассмотрите угловую скорость вращения тела в физике: определение, как объект вращается с угловой скоростью, формула решения задач, угловая и линейная скорость.
Чтобы проверить стремительность вращения тела, представим угловую скорость ω как скорость изменения угла:
Чем больше угол поворота за предложенный временной промежуток, тем выше угловая скорость. Единица – радиан в секунду.
Угловая скорость (ω) соответствует линейной (v). Чтобы отыскать точное соотношение между ними, рассмотрим углубление на вращающемся компакт-диске. Оно смещает длину дуги Δs за период Δt и поэтому обладает линейной скоростью v = Δs/Δt.
Из Δθ = (Δs)/r видно, что Δs = r ⋅ Δθ. Подставим в формулу для v, и видим:
v = (r ⋅ Δθ)/(Δt) = r (Δθ/Δt) = rω.
Это можно описать двумя путями: v = rω или ω = v/r.
Из первого видно, что линейная скорость (v) расположена пропорционально дистанции от центра вращения, поэтому ее максимум достигает для точки на ободе. На краю мы можем назвать ее тангенциальной скоростью.
Второе можно рассмотреть на перемещении машины. Обратите внимание на шину. Скорость точки в центре совпадает с показателями v машины. Чем быстрее движение, тем больше оборотов совершает шина, а значит v = rω. Точно также, шина большего радиуса, вращающаяся с той же угловой скоростью (ω), будет повышать линейную скорость (v).
Машина, смещающаяся вправо со скоростью v, обладает шиной с угловой скоростью ω. Скорость протектора шины относительно оси приравнивается к v так же, как если бы машину приподняли. Получается, что транспорт перемещается вперед с линейной скоростью v = rω (r – радиус шины). Большая угловая скорость шины приводит к повышению скорости автомобиля