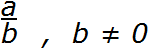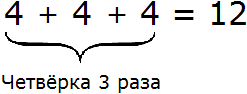Что такое операция в алгебре
Основные операции
Ещё пример. Число 11 меньше, чем число 15. Эту фразу можно записать так:
В математике с помощью отношений можно записывать законы, формулы, уравнения и функции. Можно записать, что одно выражение равно другому, либо какое-то действие недопустимо по отношению к какому-нибудь объекту, числу, закону.
Например, знаменитая фраза «на ноль делить нельзя» записывается так:
Не будем опережать события и забегать вперёд. Просто скажем, что в этом выражении вместо a и b могут стоять любые числа. Но потом говорится, что b не должно быть равным нулю.
Знак равенства = стáвится между величинами и говорит о том, что эти величины равны между собой.
Ещё пример: если один большой арбуз весит 20 кг, а два маленьких арбуза весят по 10 кг каждый, то между арбузом в 20 кг и двумя арбузами по 10 кг можно поставить знак равенства. Это отношение можно прочитать так: «один арбуз весом в 20 килограмм равен весу двух арбузов, каждый из которых весит 10 кг». Ведь 20 кг = 10 кг + 10 кг.
Знак не равно ≠ ставится между величинами тогда, когда они не равны между собой.
Вы можете осмотреться вокруг себя и найти множество примеров отношений, которые можно истолковать с точки зрения математики.
Операция сложения
Операция сложения обозначается знаком «плюс» (+) и используется, когда складывают числа.
Числа, которые складывают называются слагаемыми. Число, которое получается в результате их сложения, называется суммой.
Например, сложим числа 3 и 2.
Записываем 3 + 2 = 5
В этом примере 3 − это слагаемое, 2 − второе слагаемое, 5 − сумма.
В будущем придётся складывать довольно большие числа. Но сложение этих больших чисел в конечном итоге будет сводиться к тому, чтобы сложить маленькие.
Поэтому нужно научиться складывать маленькие числа в диапазоне от 0 до 9. Например:
Можете потренироваться, записав в тетради несколько простых примеров. Поверьте, ничего постыдного в этом нет.
Операция вычитания
Операция вычитания обозначается знаком «минус» (−) и используется когда из одного числа вычитают другое.
Число, из которого вычитают другое число, называется уменьшаемым. Число, которое вычитают из уменьшаемого числа, называется вычитаемым. Число, которое получается в результате, называется разностью.
Например, вычтем из числа 10 число 2.
В этом примере число 10 − это уменьшаемое, число 2 − вычитаемое, а число 8 − разность.
Операция умножения
Обозначается знаком умножения (×) и используется когда одно число умножается на другое. Слово умножение говорит само за себя — какое-то число увеличивается в определенное количество раз, то есть мнóжится.
Например, запись 4 × 3 означает, что четверка в ходе операции умножения будет увеличена в три раза.
Число, которое увеличивают, называется множимым. Число, которое показывает во сколько раз нужно увеличить множимое, называется множителем. Число, которое получается в результате называется произведением.
Например, умножим число 4 на 3.
В этом примере 4 − это множимое, 3 − множитель, 12 − произведение.
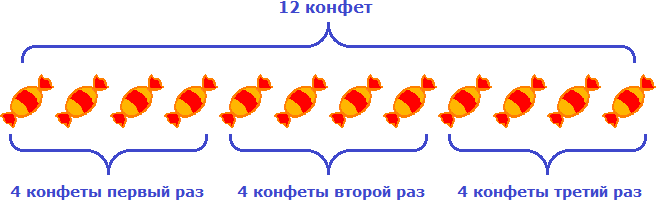
Запись 4 × 3 можно понимать как «повторить число 4 три раза». Например, если у нас имеются четыре конфеты и мы повторим их три раза, то полýчится двенадцать конфет:
Другими словами, умножение 4 на 3 можно представить как сумму трёх четвёрок:
Умножение можно понимать и другим образом, а именно как взятие чего-то определенное количество раз.
Допустим, в вазе лежат конфеты. Возьмём четыре конфеты один раз:
У нас в руках окажется четыре конфеты.
Попробуем взять четыре конфеты 2 раза:
У нас в руках окажется восемь конфет.
Попробуем взять четыре конфеты ноль раз, то есть ни разу:
У нас на руках не окажется конфет, поскольку мы ни разу их не взяли. Поэтому умножение любого числа на ноль даёт в ответе ноль.
В некоторых книгах множимое и множитель называют одним общим словом — сомножители. Например, в записи 4 × 3 множимым является 4, а множителем 3, но эти два числа ещё можно назвать сомножителями. Ошибкой это не будет.
Операция деления
Обозначается знаком деления (÷ или : ) и используется когда делят числа.
Число, которое делят называют делимым. Число, которое указывает на сколько частей делят делимое, называется делителем. Число, которое получается в результате, называется частным.
Например, разделим число 10 на 2.
В этом примере число 10 − это делимое, число 2 − делитель, число 5 − частное.
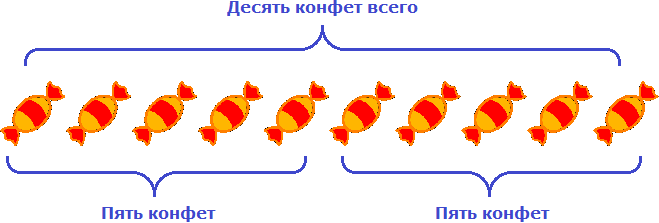
Если у нас имеются десять конфет и мы разделим их на две равные части, то в каждой части полýчится по пять конфет:
Так можно понять смысл записи 10 : 2 = 5.
Задания для самостоятельного решения
Большинство людей решат эти задания в уме что конечно похвально. Однако, рекомендуется выполнить эти задания именно в тетради, взяв в руку карандаш. К математике следует привыкать посредством решения простых примеров.
АЛГЕБРАИЧЕСКАЯ ОПЕРАЦИЯ,
n-й декартовой степени множества Ав само множество А. Число пназ. где 
Смотреть что такое «АЛГЕБРАИЧЕСКАЯ ОПЕРАЦИЯ,» в других словарях:
АЛГЕБРАИЧЕСКАЯ ОПЕРАЦИЯ — АЛГЕБРАИЧЕСКАЯ ОПЕРАЦИЯ, операция обычной алгебры, т.е. арифметические действия сложения, вычитания, умножения и деления. Операции с бесконечными рядами и функциями типа log х не являются алгебраическими они зависят от наличия пределов. Термин… … Научно-технический энциклопедический словарь
Алгебраическая система — (или алгебраическая структура) в универсальной алгебре множество (носитель) с заданным на нём набором операций и отношений (сигнатура), удовлетворяющим некоторой системе аксиом. Алгебраическая система с пустым множеством отношений… … Википедия
АЛГЕБРАИЧЕСКАЯ СИСТЕМА — множество с определенными на нем операциями и отношениями. А. с. принадлежат к числу основных математич. структур и имеют глубоко разработанную общую теорию, сформировавшуюся в начале 50 х гг. 20 в. на грани между алгеброй и математич. логикой.… … Математическая энциклопедия
математическая операция — ▲ операция ↑ математический операции, у которых исходные операнды и результат имеют одинаковую размерность: сложение, вычитание операции, у которых операнды имеют неодинаковую размерность: умножение … Идеографический словарь русского языка
НУЛЬ — 1) Число, обладающее тем свойством, что любое (действительное или комплексное) число при сложении с ним не меняется. Обозначается символом 0. Произведение любого числа на Н. равно Н.: Если произведение двух чисел равно Н., то один из сомножителей … Математическая энциклопедия
Дифференцирование — Под термином дифференцирование могут подразумевать различные родственные понятия. Дифференцирование операция взятия полной или частной производной функции. Дифференцирование линейное отображение, удовлетворяющее тождеству Лейбница.… … Википедия
КОМПОЗИЦИЯ — бинарная алгебраическая операция. Напр., К. (или суперпозицией) двух функций f(x)и g(x)наз. функция h(x)=f[g Предметом рассмотрения в абстрактной алгебре являются произвольные множества с заданными на них операциями. При этом природа множеств и операций может существенно отличаться от привычных числовых множеств и известных операций над числами. Мы уже сталкивались с операциями над множествами и бинарными отношениями, которые оказались в чем-то похожими на операции над числами, но в то же время проявились и их существенные отличия. В дискретной математике разрабатываются алгоритмы и вычислительные методы, позволяющие манипулировать сложно организованными нечисловыми структурами. Проблема работы с такими объектами возникла в связи с развитием современных информационных технологий и переходом от собственно вычислений (т.е. операций над числами) к обработке сложных структур данных. Так, проблемы программирования и машинного перевода привели к задачам работы с языковыми структурами, проблемы автоматизации проектирования — к задачам обработки графических объектов. Современная дискретная математика проникнута алгебраическим духом, поскольку оказалось, что именно на алгебраической базе наиболее удобно разрабатывать общие подходы к работе с объектами различной природы. Множество векторов в пространстве с операцией сложения векторов, операцией векторного умножения, множество квадратных матриц с операциями сложения или умножения, множество функций с операцией сложения — вот примеры некоторых множеств с операциями, рассматривающихся в различных разделах математики. Выясним, что общего есть в свойствах операций на этих множествах и в чем их различие. Для n-арной операции используют обозначение Наиболее важными в алгебре и, следовательно, наиболее исследованными являются бинарные операции. Примерами таких операций могут служить сложение и умножение чисел, сложение и умножение матриц, сложение векторов линейного пространства. Операция сложения, заданная на множестве натуральных чисел, является ассоциативной и коммутативной. Операция умножения матриц ассоциативна, но не коммутативна. Идемпотентными являются операции объединения и пересечения множеств. Пример 2.1. а. На множестве целых чисел нулем относительно операции умножения будет число 0. Однако левого нуля в этом множестве нет, так как иначе он совпадал бы с правым нулем и был бы единственным. Но правых нулей имеется больше одного. Пример 2.2. Нейтральным элементом относительно операции умножения на множестве натуральных чисел является число 1. На множестве целых чисел нейтральным элементом относительно операции сложения будет число 0. Поскольку правых нейтральных элементов несколько, то левого нейтрального элемента по этой операции нет, так как иначе существовал бы единственный нейтральный элемент (левый и правый). Следует заметить, что не для всякой бинарной операции нули и нейтральные элементы (левые и правые, в частности), существуют. Рассмотрим некоторые примеры бинарных операций на множествах. Пример 2.3. а. Пусть — универсальное множество. Теоретико-множественные операции на множестве являются идемпотентными, ассоциативными и коммутативными, причем пустое множество является нулем относительно пересечения и нейтральным элементом относительно объединения тогда как универсальное множество есть нуль относительно объединения и нейтральный элемент относительно пересечения б. На множестве всех бинарных отношений на множестве операция композиции отношений является ассоциативной, но не коммутативной, а диагональ множества будет нейтральным элементом относительно этой операции. Действительно, для любого отображения и любого имеем Рассмотренные выше примеры множеств с операциями приводят к следующим определениям. Замечание 2.1. Операции, включенные в сигнатуру, заданы как некоторые специальные отображения. Однако при этом не оговариваются свойства, которыми обладают операг ции на носителе. Например, они могут быть ассоциативными, коммутативными и т.д. При задании алгебр свойства операций обычно указывают дополнительно. Если существует нейтральный элемент относительно операции, то его можно задать как нульарную операцию на носителе и включить в сигнатуру, а можно не включать и описать как свойство соответствующей операции. Таким образом, одну и ту же алгебру можно задавать по-разному. Ниже приведены примеры различных описаний конкретных алгебр. Пример 2.4. а. Рассмотрим алгебру б. Для любого множества можно определить алгебру в. На множестве действительных чисел можно, например, определить такую алгебру: сигнатура которой состоит из операций сложения, умножения, а также двух нульарных операций, обозначающих два особых числа 0 и 1. Обратим внимание на то, что числа 0 и 1 в данном случае являются соответственно нулем и нейтральным элементом относительно умножения, а число 0 также играет роль нейтрального элемента относительно сложения. Мы применили понятие нульарнои операции, чтобы в обозначении алгебры отразить элементы со специальными свойствами. г. Все предыдущие примеры алгебр были алгебрами с конечной сигнатурой, т.е. с сигнатурой, состоящей из конечного числа операций. Однако несложно построить пример алгебры с бесконечной сигнатурой. Например, алгебра на множестве действительных чисел с операцией возведения в натуральную степень имеет счетную сигнатуру. Далее будут приведены примеры алгебр и с несчетными сигнатурами. Определяя алгебру, следует помнить, что результат применения любой операции обязательно должен принадлежать тому же множеству, что и ее аргументы. Например, пару из множества всех свободных векторов в пространстве и операции скалярного умножения векторов нельзя рассматривать как алгебру, так как скалярное произведение двух векторов не есть вектор. Заменив скалярное умножение векторным, получим алгебру. Точно так же множество действительных чисел с операцией деления действительных чисел не является алгеброй, поскольку результат деления не определен при нулевом делителе. Пара же есть алгебра. Договоримся, определяя конкретную алгебру, записывать ее сигнатуру без фигурных скобок, перечисляя после обозначения носителя все операции. Так, в примере 2.4.а первая алгебра может быть записана как Алгебра и алгебра в примере 2.4.а не являются однотипными, так как их сигнатуры состоят из разного числа операций и между ними установить взаимно однозначное соответствие нельзя. Операция — отображение, ставящее в соответствие одному или нескольким элементам множества (аргументам) другой элемент (значение). Термин «операция» как правило применяется к арифметическим или логическим действиям, в отличие от термина «оператор», который чаще применяется к некоторым отображением множества на себя, имеющим замечательные свойства. Операция — отображение, областью определения которого является прямое произведение нескольких множеств. Арность операции — количество множеств, декартово произведение которых является её областью определения. Для операций могут быть характерны следующие свойства: Операция — В Викисловаре есть статья «операция» Операция (лат. operatio, действие) действие … Википедия МАТЕМАТИКА — Математику обычно определяют, перечисляя названия некоторых из ее традиционных разделов. Прежде всего, это арифметика, которая занимается изучением чисел, отношений между ними и правил действий над числами. Факты арифметики допускают различные… … Энциклопедия Кольера Математика инков — Кипукамайок из книги Гуамана Пома де Айяла «Первая Новая Хроника и Доброе Правление». Слева у ног кипукамайока юпана, содержащая вычисления священного числа для песни «Сумак Ньюста» (в оригинале рукописи рисунок не цветной, а чёрно белый;… … Википедия Сложение (математика) — У этого термина существуют и другие значения, см. Сложение (значения). Сложение (прибавление) одна из основных операций (действий) в разных разделах математики, позволяющая объединить два объекта (в простейшем случае два числа). Более … Википедия Вектор (математика) — Вектор У этого термина существуют и другие значения, см. Вектор … Википедия Теория функциональных систем (дискретная математика) — У этого термина существуют и другие значения, см. Теория функциональных систем (значения). Теория функциональных систем раздел дискретной математики, занимающийся изучением функций, описывающих работу дискретных преобразователей. В теории… … Википедия Группа (математика) — Теория групп … Википедия Кольцо (математика) — У этого термина существуют и другие значения, см. Кольцо. В абстрактной алгебре кольцо это один из наиболее часто встречающихся видов алгебраической структуры. Простейшими примерами колец являются алгебры чисел (целых, вещественных,… … Википедия Деление (математика) — Запрос «Деление» перенаправляется сюда; для просмотра других значений см. Деление. Деление (операция деле … Википедия Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы. Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики. Алгебра логики — это раздел математической логики, который исследует операции над высказываниями. Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных. Основные законы алгебры логики представлены в таблице: В информатике предоставляется два вида высказываний: простое и сложное. Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное. Нью-Йорк — столица США (ложное); в России 1117 городов (верное). Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами. Идёт дождь, а у меня нет зонта.Алгебраические структуры и операции
Понятие алгебраической структуры
Нейтральные элементы относительно операции
Примеры бинарных операций на множествах
Сигнатура алгебры
Однотипные алгебры
Операция (математика)
Содержание
Определение
Связанные определения
Свойства
См. также
Полезное
Смотреть что такое «Операция (математика)» в других словарях:
Что такое алгебра и алгебра логики
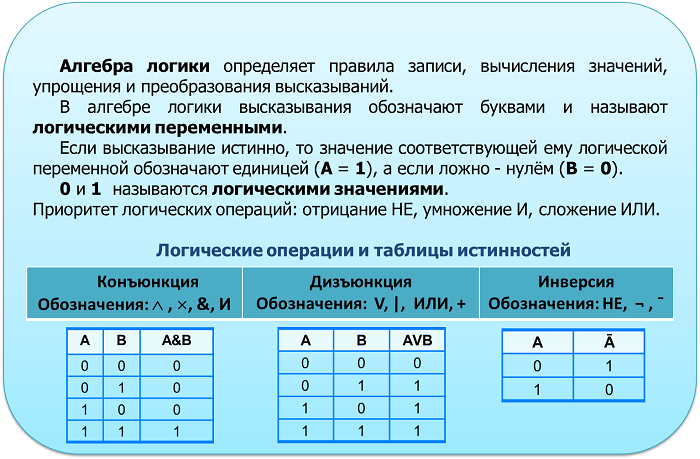
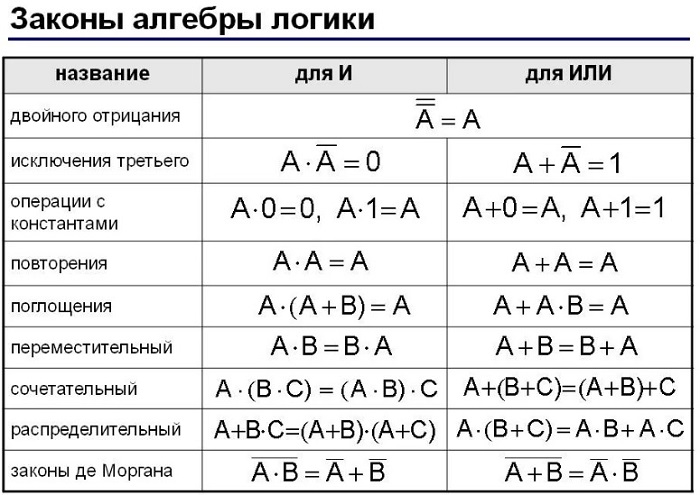
Законы алгебры логики
Логические выражения
Основные логические операции
Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.
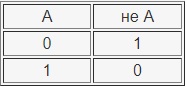
Логическое отрицание (инверсия) —НЕ
Таблица истинности инверсии:
Результаты операции НЕ следующие:
если исходное выражение истинно, то результат его отрицания будет ложным;
если исходное выражение ложно, то результат его отрицания будет истинным.
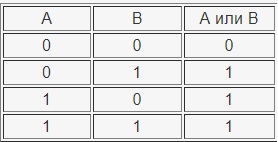
Логическое сложение (дизъюнкция, объединение) — ИЛИ
Понятие «Логическое ИЛИ» также можно заменить понятием «Дизъюнкция». Данная операция обозначается знаками — ИЛИ, OR, ||, |.
Но есть небольшое отличие: в «Логическом И» результат отрицания равен единице, если оба обозначения равны единице, а в «Логическом ИЛИ» итог равен единице, если одно из обозначений равно единице.
Таблица истинности операции ИЛИ:
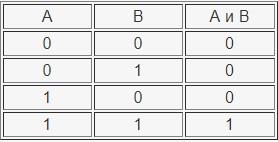
Логическое умножение(конъюнкция) — И
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.
За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).
При всех остальных значениях операция будет ложной.
Таблица истинности операции И приведена ниже:
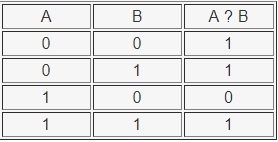
Логическое следование (импликация) — ЕСЛИ ТО
Данная программа имеет также название «Импликация». Она образуется из двух высказываний, которые соединяет: «если. то».
Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.
Таблица истинности операции ЕСЛИ ТО выглядит так:
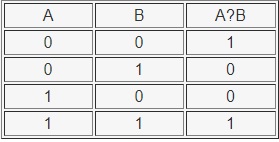
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.
И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.
Таблица истинности операции эквивалентности: