Что такое операция в информатике
Операция (программирование)
Опера́ция — конструкция в языках программирования, аналогичная по записи математическим операциям, то есть специальный способ записи некоторых действий. Наиболее часто применяются арифметические, логические и строковые операции. В отличие от функций, операции часто являются базовыми элементами языка и обозначаются различными символами пунктуации, а не алфавитно-цифровыми; они имеют специальный инфиксный синтаксис и нестандартные правила передачи аргументов. Терминология, однако, несколько отличается от языка к языку.
Содержание
Операция и инструкция
Операция и функция
Фактически, операция — это та же функция, но записываемая особым образом. По этой причине логично иметь возможность определять операции для произвольных типов таким же образом, как и методы — чтобы можно было работать с ними точно так же, как и с элементарными типами. Эта возможность называется «перегрузка операций» и присутствует в большинстве языков 4—5 поколений. В таких языках транслятор, фактически, подставляет вместо выполнения операции вызов соответствующей ей функции.
Типы операций
Операции делятся по количеству принимаемых аргументов на:
Синтаксис операций
Поскольку операции аналогичны по записи алгебраическим выражениям, для них, как и для последних, существует 3 варианта синтаксиса:
Для бинарных и тернарных (с 3 операндами) операций в подавляющем большинстве случаев используют инфиксную нотацию — по той простой причине, что она принята в математике и наиболее привычна большинству людей. Для унарных операций инфиксной нотации не существует, и, как правило, используется префиксная.
Список типовых операций
Операции обычно переходят из языков в родственные — например, операции языка С присутствуют в языках C++, Java, JavaScript и многих других.
проверка на неравенство
меньше, меньше или равно
См. также
Ссылки
Полезное
Смотреть что такое «Операция (программирование)» в других словарях:
Операция — В Викисловаре есть статья «операция» Операция (лат. operatio, действие) действие … Википедия
программирование — я, ср. programmer.1. Раздел вычислительной математики и техники, связанный с эксплуатацией электронных машин, с автоматическим программным управлением; составлением программ 10. БАС 1. 2. Действие по знач. гл. программировать. Программирование… … Исторический словарь галлицизмов русского языка
ПРОГРАММИРОВАНИЕ ПАРАЛЛЕЛЬНОЕ — раздел программирования, связанный с изучением и разработкой методов и средств для: а) адекватного описания в программах естественного параллелизма моделируемых в ЭВМ и управляемых ЭВМ систем и процессов, б) распараллеливания обработки информации … Математическая энциклопедия
программирование — я; ср. 1. к Программировать. П. производства. Операция программирования. 2. Раздел прикладной математики и вычислительной техники, разрабатывающий методы составления программ для ЭВМ. Заниматься программированием. Специалист по программированию.… … Энциклопедический словарь
программирование — я; ср. 1) к программировать Программи/рование производства. Операция программирования. 2) Раздел прикладной математики и вычислительной техники, разрабатывающий методы составления программ для ЭВМ. Заниматься программированием. Специалист по… … Словарь многих выражений
Битовая операция (значения) — Битовая операция: Битовая операция (теория алгоритмов) (или элементарная операция [1]) в теории алгоритмов, криптографии запись знаков 0, 1, плюс, минус, скобка; сложение, вычитание и умножение двух битов (числа записаны в двоичной системе… … Википедия
Оператор (программирование) — У этого термина существуют и другие значения, см. оператор. Из за путаницы с терминологией словом «оператор» в программировании нередко обозначают операцию (англ. operator), см. Операция (программирование). Инструкция или оператор… … Википедия
Комбинаторное программирование — Комбинáторное программирование (англ. function level programming) это парадигма программирования, не требующая явного упоминания аргументов определяемой функции (программы) и использующая вместо переменных комбинаторы и композицию… … Википедия
Логические операции. ➞ Что такое конъюнкция, дизъюнкция, импликация
Тот, кто хочет подробно разбираться в цифровых технологиях должен понимать основы такой темы, как алгебра логики. В этой статье будут разобраны основные определения, а также показаны самые важные логические операции, такие как конъюнкция, дизъюнкция, импликация и т.д.
Основные положения
Для начала следует разобраться, для чего нужна алгебра логики – главным образом, этот раздел математики и информатики, нужен для работы с логическими выражениями и высказываниями.
Логическим высказыванием называется утверждение (или запись), которое мы можем однозначно классифицировать, как истинное или ложное (1 или 0 в информатике).
Примером таким высказываний будут являться:
Логические высказывания делятся на два типа — простые и сложные.
В алгебре логики, как простые, так и сложные высказываниями описываются булевыми выражениями.
Булево выражение – это символическое (знаковое) описание высказывания.
Операции
Ниже рассмотрим основные операции, которые применяются в булевой алгебре. Их хватит, чтобы упростить львиную долю всех выражений, которые Вам встретятся.
Конъюнкция
Конъюнкция (булево умножение) — функция, по своему смыслу приближенная к союзу «И». При выполнении конъюнкции результат истинен (равен 1) тогда и только тогда, когда истинны ВСЕ переменные. Если хотя бы одно из высказываний ложно, то ложно и всё выражение (равно 0).
Функция может работать как с двумя операндами (высказываниями), так и с тремя, четырьмя и т.д. В математике обозначается с помощью знаков \( \wedge \) и &. Обозначение в языках программирования AND, &&. Таблица истинности для двух операндов:
Дизъюнкция
Дизъюнкцией называется функция булева сложения. По смыслу дизъюнкция приближена к союзу «ИЛИ». В результате выполнения данной функции результирующие выражение является истинным, когда хотя бы одно из высказываний в этом выражении тоже истинно.
Булево сложение, также как и умножение, может работать с произвольным количеством операндов. В математике обозначается как V, а в программировании с помощью OR или I.
Инверсия
Логическое отрицание – функция, работающая с одним высказыванием, и заменяющая истину на ложь, а ложь на истину. В математике обозначается с помощью черты над значением, а в программирование и информатике с помощью слова NOT.
Импликация
Также называется булевым следованием. В русском языке данной функции соответствует оборот «Если …, то …». Например, если на улице гремит гром, то стоит пасмурная погода.
Эквивалентность
Булева тождественность или равенство. На простом языке будет обозначено как «… эквивалентно (равно) …». Результат будет истинным тогда, когда все значения в выражении будут иметь одинаковую истинность.
Обозначается с помощью трех черточек или ⟺.
Порядок выполнения операций
Логические операции выполняются в следующем порядке:
Если в формуле указаны скобки, то порядок выполнения действий в скобках точно такой же, как написано выше.
Пример
Дано два отрезка B = [2,10], C = [6,14]. Из предложенных вариантов ответа выберите такой отрезок A, что формула \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) истинна при любом значении z. Варианты ответа:
Решение: Подставим в уравнение \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) =1 значения B и C и составим таблицу истинности:
Получившаяся формула \( ((z \in A) \Longrightarrow (z \in [2,10])) \vee (z \in [6,14])=1 \). По условию \( z \in A \)=1.
Таблица истинности для всех отрезков:
Ответ: A = [3,11].
Видео
Заключение
Вот Вы и познакомились с основными логическими операциями и понятиями и знаете, что такое булево сложение и умножение. Если вас заинтересовала данная тема, то можете изучить булевы законы. Эти законы не проходятся в рамках школьной программы и служат для упрощения сложных выражений.
Операция (программирование)
Наиболее часто применяются арифметические, логические и строковые операции. В отличие от функций, операции часто являются базовыми элементами языка и обозначаются различными символами пунктуации, а не алфавитно-цифровыми; они имеют специальный инфиксный синтаксис и нестандартные правила передачи аргументов. Терминология, однако, несколько отличается от языка к языку.
Связанные понятия
Из-за путаницы с терминологией словом «оператор» в программировании нередко обозначают операцию (англ. operator), см. Операция (программирование).Инстру́кция или опера́тор (англ. statement) — наименьшая автономная часть языка программирования; команда или набор команд. Программа обычно представляет собой последовательность инструкций.
Упоминания в литературе
Связанные понятия (продолжение)
В языках программирования объявле́ние (англ. declaration) включает в себя указание идентификатора, типа, а также других аспектов элементов языка, например, переменных и функций. Объявление используется, чтобы уведомить компилятор о существовании элемента; это весьма важно для многих языков (например, таких как Си), требующих объявления переменных перед их использованием.
В информатике и теории автоматов состояние цифровой логической схемы или компьютерной программы является техническим термином для всей хранимой информации, к которой схема или программа в данный момент времени имеет доступ. Вывод данных цифровой схемы или компьютерной программы в любой момент времени полностью определяется его текущими входными данными и его состоянием.
Побо́чные эффе́кты (англ. side effects) — любые действия работающей программы, изменяющие среду выполнения (англ. execution environment). Например, к побочным эффектам относятся.
По одной из классификаций, языки программирования неформально делятся на сильно и слабо типизированные (англ. strongly and weakly typed), то есть обладающие сильной или слабой системой типов. Эти термины не являются однозначно трактуемыми, и чаще всего используются для указания на достоинства и недостатки конкретного языка. Существуют более конкретные понятия, которые и приводят к называнию тех или иных систем типов «сильными» или «слабыми».
В логике логи́ческими опера́циями называют действия, вследствие которых порождаются новые понятия, с использованием уже существующих. В более узком смысле, понятие логической операции используется в математической логике и программировании.
В информатике, спи́сок (англ. list) — это абстрактный тип данных, представляющий собой упорядоченный набор значений, в котором некоторое значение может встречаться более одного раза. Экземпляр списка является компьютерной реализацией математического понятия конечной последовательности.
Что такое операция в информатике
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Основные логические операции
Логические операции в создании компьютерных программ — действия, которые производятся над входными данными. Такие функции производятся над сигналами булевского типа, то есть над примитивными выражениями, имеющими только два возможных значения: истина или ложь.
Виды операций
В программировании выделяют следующие виды функций:
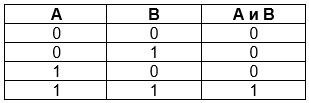
Логическое умножение (конъюнкция)
Конъюнкция — это действие, в результате которого каждым двум входным данным соответствует одно новое высказывание. Истинное значение на выходе получается, когда оба входных значения истинны.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Таблица истинности для логического умножения выглядит так:
A, B — исходные данные;
A и B — значение, приобретаемое в результате реализации конъюнкции.
Из таблицы следуют свойства логического умножения:
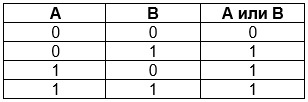
Логическое сложение (дизъюнкция)
Дизъюнкция — это булева функция, в итоге которой выходные данные будут ложными только при ложности всех исходных выражений.
Таблица истинности логического сложения:
A, B — входная информация;
A или B — значение, приобретаемое в результате выполнения дизъюнкции.
Для дизъюнкции справедливы следующие утверждения:
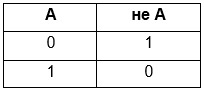
Логическое отрицание (инверсия)
Инверсия — выражение, ставящее в соответствие одному значению противоположное.
Условное обозначение логического отрицания: с помощью частицы «не», символов ¯, \(\neg.\)
Таблица истинности инверсии:
A — исходные данные;
не A — значение, приобретаемое в результате логического отрицания.
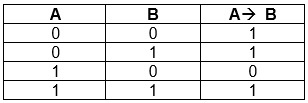
Логическое следование (импликация)
Импликация — это булева операция, ложная лишь тогда, когда первая исходная переменная является истиной, а вторая — ложью.
Следование записывается с помощью знака \(\rightarrow.\)
Таблица истинности для импликации:
A — входная информация, означающая условие;
B — входная информация, означающая следствие;
A → B — значение, приобретаемое в результате импликации.
По своему употреблению данная связка схожа со значением союзов «если. то. ».
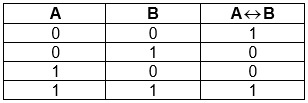
Логическая равнозначность (эквивалентность)
Эквивалентность — выражение, являющееся истинным лишь в случае равенства двух входных элементов.
Таблица истинности для равнозначности:
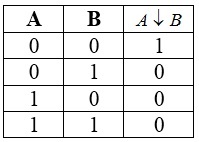
Стрелка Пирса
Стрелка Пирса — двухместное логическое действие со следующей последовательностью: сначала над исходными показаниями производится дизъюнкция, затем происходит отрицание полученного результата.
Данная манипуляция является отрицание логического сложения. Свое название рассматриваемая функция получила от своего автора — американского ученого Чарльза Пирса.
Таблица истинности для этой операции следующая:
Особенность стрелки Пирса заключается в ее возможности строить другие булевы функции.
Пример
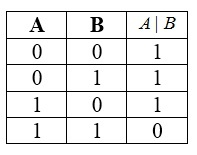
Штрих Шеффера
Штрих Шеффера — это действие, приводящее к ложному итогу лишь при истинности обоих исходных данных. По порядку выполнения операций эта функция эквивалентна отрицанию конъюнкции.
Символ Шеффера назван по фамилии своего создателя — американского логика Генри Шеффера — и обозначается посредством знака \(\vert.\)
Таблица истинности для данной функции:
С помощью штриха Шеффера можно воспроизвести другие логические манипуляции.
Пример
Порядок выполнения операций
В составном логическом выражении действия выполняются в такой последовательности:
Для построения нужного порядка, как и в математических выражениях, используют скобки.