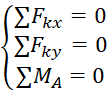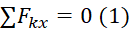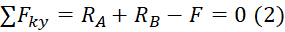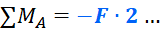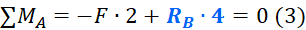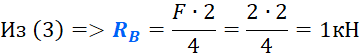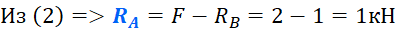Что такое опорная реакция

Как определить реакции опор или найти опорные реакции: для балки или рамы

Что такое реакция опоры или опорная реакция?

Реакция опоры или опорная реакция – это силовой фактор, возникающий в опоре, от действия на конструкцию внешней нагрузки. В опорах, как правило, возникают реактивные силы, которые для удобства ручного расчета раскладываются на две составляющие: вертикальную и горизонтальную проекции. В жестких заделках, которые ограничивают все степени свободы конструкций, в том числе поворот сечений, также могут появляться реактивные моменты.

Зачем определять реакции опор?

На элементы конструкций всегда наложены какие-то связи, в виде опор, жестких заделок, стержней, которые ограничивают степени свободы конструкций. Под действием внешней нагрузки в этих связях возникают реакции. И эти реакции опор нужно обязательно учитывать при расчетах на прочность, жесткость и т. д., так как они являются внешними нагрузками. Практически любая задача по сопромату начинается с нахождения реакций связей, именно поэтому статья будет одной из первых на этом сайте.

Пример определения опорных реакций для балки

Давайте рассмотрим пример, на котором я покажу как определяются реакции опор. Причем, постараюсь объяснить максимально просто, буквально на пальцах.

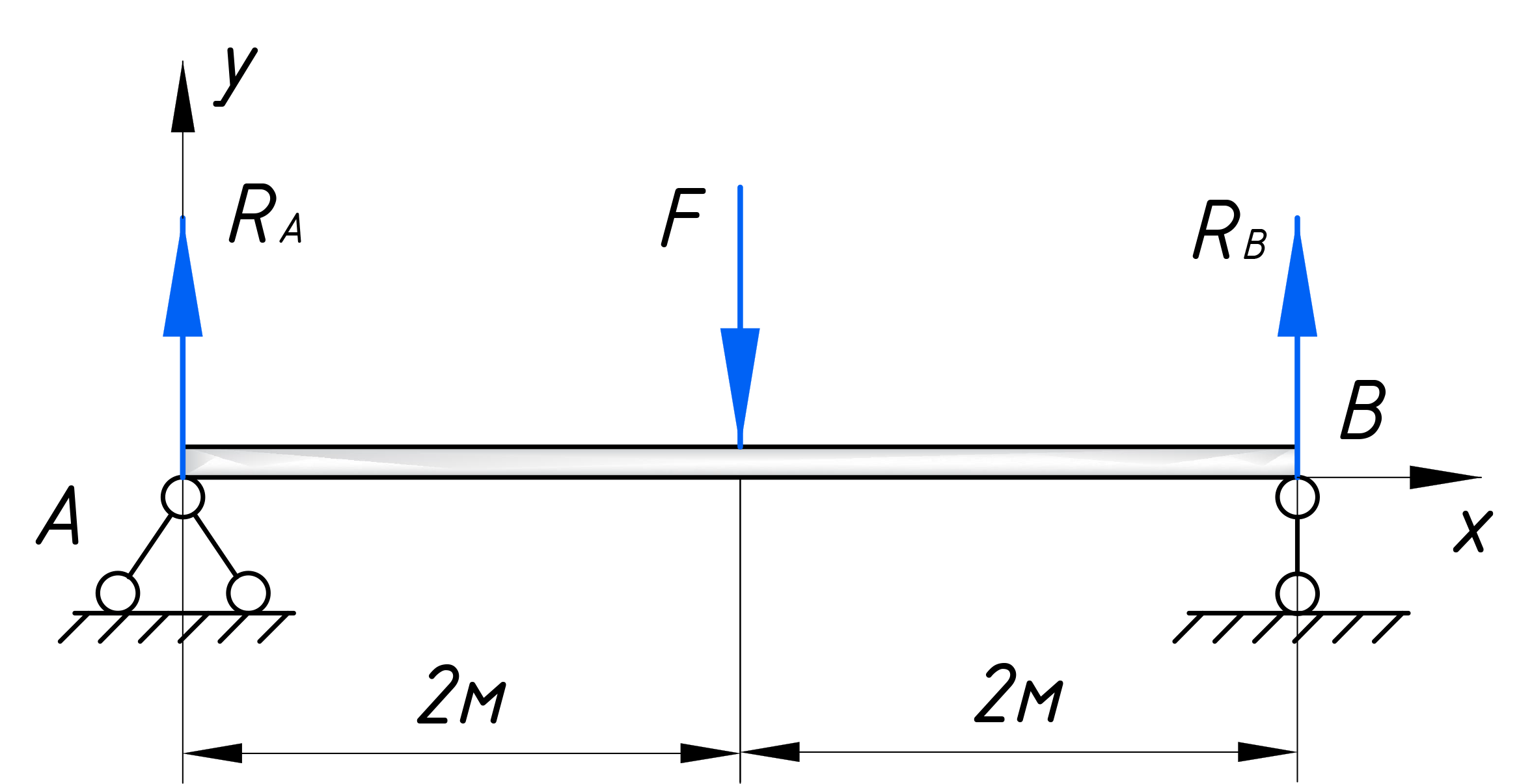
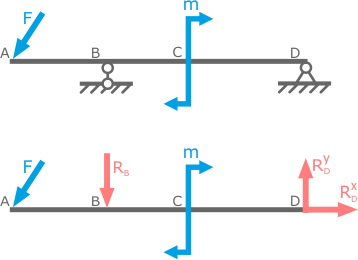
Возьмем простую балку, загруженную сосредоточенной силой F, под действием которой в опорах появляются реакции R_A и R_B. Также сразу вводим систему координат x, y:

Чтобы узнать численное значение эти реакций, воспользуемся первой формой уравнений равновесия:

Первое уравнение равновесия

Записываем первое уравнение. Так как оси x не параллельна ни одна из сил, то соответственно сумма проекций сил на эту ось будет равна нулю:

Таким будет первое уравнение для этой расчетной схемы.

Второе уравнение равновесия

Второе уравнение, связанно с проекциями на вертикальную ось. Здесь все намного лучше, все силы параллельны этой оси, а значит дадут проекции. Вопрос только с каким знаком, каждая сила пойдет в уравнение. Если направление силы, совпадает с направлением оси, то в уравнение она пойдет со знаком «плюс» (R_A и R_B). Если же сила направленна в противоположную сторону, как F, в нашем случае, то в уравнении будем записывать ее с минусом. Таким образом, получим второе уравнение равновесия:

Как видите, во втором уравнении у нас находится 2 неизвестные реакции. Чтобы, наконец, решить задачу, давайте запишем третье уравнение равновесия.

Третье уравнение равновесия

Это уравнение отличается от первых двух, так как тут речь идет о моментах. Напомню, момент – это произведение силы на плечо. В свою очередь, плечо – это перпендикуляр, опущенный от центра момента до линии действия силы. То есть это кратчайшее расстояние от центра момента до силы. В качестве центра моментов у нас назначена точка A, по условию сумма моментов всех сил должна быть равна нулю относительно этой точки.

Начинаем рассуждать и записывать уравнение. Реакция R_A не дает момента, относительно точки А, так как линия действия этой силы пересекает эту точку и соответственно плечо равно нулю. А там, где нет плеча, нет и момента.

Сила F, относительно точки А, создает момент равный:

Обратите внимание, плечо в данном случае равно 2 метрам. Кроме того, важен знак момента, для этого традиционно используется правило, которое продвинутым студентам известно еще с теоретической механики:

Для силы F, как видите, момент отрицательный:

Реакция опоры — R_B, создает момент равный R_B · 4, так как сила поворачивает против часовой стрелки, то в уравнение записываем его со знаком плюс:

Вычисление реакций опор

Вот собственно и все, все уравнения составлены. Теперь осталось только решить их и найти искомые значения реакций опор (F=2 кН):

В этой статье, мы рассмотрели достаточно простой пример. Если вы хотите развить свои навыки по определению реакций опор, узнать различные хитрости по их нахождению, научится определять реакции, когда на конструкцию действуют силы под различными углами, учитывать в уравнениях сосредоточенные моменты и распределенную нагрузку, приступайте к изучению статьи – как определить реакции опор для балки.

Источник

Виды опор и опорных реакций

Сопромат, какие виды опор бывают и как из реальных конструкций нарисовать схематические опоры, какие реакции опор (сила реакции опоры и момент в заделке) при этом возникают и как их понять, как учесть.

Ниже видео урок, на котором я на доске объясняю все то что написано в тексте. Смотрите, может быть так вам лучше вопринимается.

Какие виды опор встречаются в жизни?

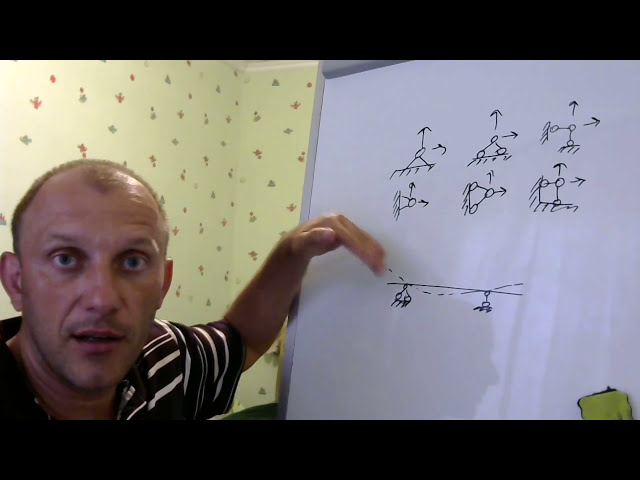
В целом опора — это такое устройство, которое сопротивляется движению. Мы же помним такое выражение к закону Ньютона: «Сила действия равна силе противодействия». Так вот в реальной жизни есть всего два вида движения: поступательное и вращательное. Остальные виды движения комбинируются. Т.е. плоскопараллельное — это сочетание поступательного и вращательного движений. Но сейчас о первых двух.

Для того чтобы тело двигалось горизонтально или вертикально — нужно приложить силу вдоль этой оси.

Для того чтобы тело вращалось относительно оси — нужно приложить момент

Чтобы зафиксировать поступательное движение — нужна соответственно опора, реакция в виде силы, а чтобы вращательное движение предотвратить — нужен момент в опорной конструкции.

Опорные реакции, Виды опор в схемах реальных конструкций

Что такое защемление балки, что такое заделка. Как сопоставить заделку на схеме (на рисунке) с закреплением балки в стену. Почему возникают моменты в заделке?

балка с жестким защемлением, такой вид опор называют заделка

Какую опору балки или стержня мы называем шарнирно подвижная опора и какая реакция при это возникает. Какую называем опору называем шарнирно неподвижная опора. Почему?

Какие опорные реакции возникают в этих опорах и как их определять.

Об этом в нашем видео уроке на тему «Виды Опор и опорные реакции. Заделка и шарнирно подвижные и неподвижные опоры, Сопромат.»

Шарнирно подвижная опора это такая опора, в которой возникает одна опорная реакция в одном направлении, вдоль стержня этой опоры.

слева шарнирно неподвижная опора, а справа шарнирно подвижная

На рисунке выше представлена обычная балка, которая изгибается под действием вертикальной силы. Обычно так обозначают опорные реакции для реальных конструкций таких как, например, бревно (балка) лежит свободно на обрезках бревна (круглых катках), просто балка лежит сверху на стене, а на ней больше, кроме силы нет ничего. Это называют еще свободное опирание. Так если линейку положить на два карандаша — это и будет точно такая же схема опирания. Но на рисунке левая опора показывает еще то, что балка (линейка на карандашах) не «уедет» свободно вдоль (по столу линейка на карандашах не поедет) потому, что в продольном направлении есть реакция на левой опоре, которая не позволяет это сделать

Источник

Опоры и опорные реакции, и их определение

Лекция №1

Тема: «Внутренние усилия в поперечных сечениях стержня»

Вопросы:

Метод сечений для определения внутренних сил

Напряжения

Опоры и опорные реакции, и их определение

Поперечная сила и изгибающий момент

Метод сечений для определения внутренних сил

Как уже отмечалось, до приложения к телу нагрузки, внутри его не возникает внутренних усилий (4-е допущение). При приложении внешних сил или моментов внутри тела появляются внутренние силовые факторы. Их определяют методом сечений. Для этого в интересующем нас месте делается мысленный разрез, отбрасывается одна часть тела (обычно та, на которую действует больше сил), а ее воздействие на оставшуюся заменяется внутренними силовыми факторами, значение которых находят из уравнений статического равновесия рассматриваемой части тела.

Возможны два варианта решения задачи:

а) внешние силы и моменты находятся в одной плоскости, проходящей через центр тяжести сечения (плоская задача);

б) внешние силы и моменты не находятся в одной плоскости (пространственная задача).

Рассмотрим плоскую задачу. Пусть на тело (рисунок 1) действует система сил, лежащих в одной плоскости и оно находится в статическом равновесии. Определим внутренние усилия в сечении 1-1. Отбрасываем правую часть тела, а ее воздействие на левую заменим на три силовые факторы: продольную силу N, направленную перпендикулярно плоскости сечения; поперечную силу Q, лежащую в плоскости сечения (на рисунке она несколько смещена вправо для того, чтобы она не сливалась с сечением); изгибающий момент М, плоскость действия которого перпендикулярна плоскости сечения.

Рисунок 1

Для нахождения внутренних силовых факторов проведем оси координат через центр тяжести сечения OX, OY и составим уравнения статического равновесия:

; ;

где и – соответственно проекции сил и на ось OY.

.

; ;

где и – соответственно проекции сил и на ось OX.

;

где a₁ и a₂ плечи сил и , т.е. кратчайшие стояния от точки 0 до направления действия сил (плечо a₂ не показано, чтобы не усложнять рисунок).

Аналогично определяют усилия в сечениях 2-2, 3-3 и т.д. по всей длине тела. Определив значения N, Q и M строят эпюры (графики) каждого внутреннего усилия в отдельности. По эпюрам находят опасное сечение (сечения). Опасным считают сечение, где одно из внутренних усилий имеет максимальное значение. Это важно при расчете брусьев постоянного сечения (стержней), так как там, где внутреннее усилие максимально, возможна потеря прочности. А если прочность обеспечена в опасном сечении, то она обеспечена для всего стержня.

При плоской задаче опасных сечений может быть три. При некоторых видах нагружения два из трех внутренних усилий могут быть равны нулю, и тогда будет одно опасное сечение. Возможен также вариант, когда все внутренние усилия имеют максимум в одном сечении. Тогда тоже будет одно опасное сечение.

Рассмотрим пространственную задачу, т.е. когда внешние силы и моменты не лежат в одной плоскости (рисунок 2).

Рисунок 2

Внутренних усилий будет шесть: три силы и три момента, т.е. одна сила и один момент относительно каждой оси координат (две силы или два момента относительно одной оси быть не может, так как они сложатся и будет результатируюшая, т.е. одна сила или момент).

Сила, перпендикулярная сечению, называется продольной N и направлена по оси Z. Сила, лежащая в плоскости сечения, называется поперечной Q. Их будет две: вдоль осей Y и X соответственно Q_y и Q_x. Эти силы можно сложить по правилу параллелограмма и получить одну силу Q. Моменты M_x и M_y действуют перпендикулярно плоскости сечения, поэтому являются изгибающими. Момент M_z лежит в плоскости сечения и называется крутящим моментом Т.

Для пространственной задачи составляется шесть уравнений статического равновесия:

; определяем ;

; определяем ;

; определяем ;

; определяем ;

; определяем ;

; определяем .

Возможны следующие частные случаи возникновения внутренних усилий в сечении:

а) только продольная сила N. Это случай растяжения (сила направлена от сечения) или сжатия (сила направлена внутрь тела);

б) только поперечная сила Q.Это случай сдвига;

в) только крутящий момент Т. Это случай кручения;

г) только изгибающий момент М_х или только изгибающий момент М_у. Это случай изгиба.

д) Несколько внутренних усилий, например, М_х и М_у вместе. Это случай сложного сопротивления.

Напряжения

Внутренние усилия действуют не в одной какой-либо точке, а распределены по всему сечению, причем интенсивность их, т.е. отношение внутреннего усилия к площади сечения, в разных точках может быть различной. Интенсивность внутренних усилий называют также механическим напряжением или просто напряжением.

Напряжение – это внутренняя сила, приходящаяся на единицу площади в данной точке данного сечения. Размерность напряжения сила/площадь. Единица измерения – паскаль.

Паскаль величина небольшая. Его можно представить как давление 100 г воды, разлитой на 1 м 2 поверхности. Прочность всех материалов измеряется в миллионах Па, поэтому применяют математическую приставку “мега”, т.е. миллион.

Рисунок 3

Полное напряжение р можно разложить на две составляющие (рисунок 3):

а) нормальную к плоскости сечения, называемую нормальным напряжением s;

б) лежащую в плоскости сечения, называемую касательным напряжением t.

Разложение полного напряжения на нормальное и касательное имеет определенный физический смысл. Нормальные напряжения возникают, когда частицы материала стремятся отдалится друг от друга или наоборот, сблизится. Касательные напряжения связаны со сдвигом частиц материала по плоскости рассматриваемого сечения.

Опоры и опорные реакции, и их определение

При расчете конструкций в основном встречаются элементы, испытывающие изгиб. Стержни, работающие преимущественно на изгиб, называют балками. Для того чтобы балка могла испытывать нагрузку и передавать ее на основание, она должна быть соединена с ним опорными связями. На практике применяют несколько типов опорных связей, или, как говорят, несколько типов опор.

Различают три основных типа опор:

а) шарнирно-подвижная опора:

б) шарнирно-неподвижная опора:

Рисунок 4

Рисунок 5

На рисунке 6 показана жесткая заделка. Она не позволяет балке ни поворачиваться, ни перемещаться. Поэтому могут возникать три опорные реакции: момент, вертикальная и горизонтальная силы. Если балка не имеет на конце опоры, то эта часть ее называется консолью.

Рисунок 6

Определим реакции опор для балки (см. рисунок 7).

Рисунок 7

где — момент от равномерно распределенной нагрузки.

Произведение q на расстояние, на котором она приложена, из условия равновесия системы равно сосредоточенной силе, приложенной посредине отрезка. Поэтому момент равен:

– момент силы F

Внешний момент m на плечо не умножается, так какэто пара сил, т.е. две равные по величине, противоположно направленные силы, имеющие постоянное плечо.

.

Проверка: Сумма всех сил на вертикальную ось Y должна быть равна нулю:

.

Источник

iSopromat.ru

Опорными называют реакции связей, возникающие в опорах под действием внешних нагрузок и удерживающие рассматриваемый элемент или конструкцию в статическом равновесии.

При расчете элементов конструкций реакции опор также выступают в качестве внешних усилий приложенных к рассматриваемому телу.

Подрообнее о реакциях в различных типах опор смотрите в нашем видео:

При этом некоторые задачи в сопромате можно решить без их определения. Это возможно в случаях, когда за расчетную схему принимается брус, закрепленный в жесткой опоре (заделке) без дополнительных опор, например, статически определимые консольные балки, стержни либо стержневые системы.

Реакции в шарнирных опорах

Реакции в шарнирных опорах могут возникать только по тем направлениям, в которых перемещение исключено:
нормально к опорной поверности и вдоль неё.

Моменты в шарнирных опорах не возникают.

Реакции в шарнирно-неподвижных опорах

В плоской шарнирно-неподвижной опоре исключены линейные перемещения во всех направлениях и возможен только поворот относительно шарнира.
Поэтому в таких опорах могут иметь место реакции, направленные нормально к поверхности и вдоль нее: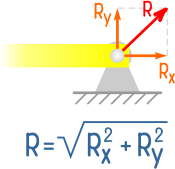

Они являются проекциями полной реакции R на вертикальную и горизонтальную оси.

Реакции в шарнирно-подвижных опорах

В шарнирно-подвижной опоре возможно поступательное перемещение вдоль одной из осей, следовательно в данном направлении реакции быть не может.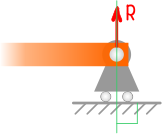

В данном случае, оставшаяся реакция по величине и направлению, будет равна полной.

Реакции в шарнире

В трехмерном шаровом шарнире аналогично, осевые проекции полной реакции R направляются вдоль всех трех осей: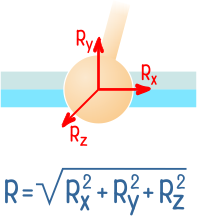

При этом, в зависимости от схемы нагружения, некоторые из проекций могут быть равны нулю.

Расчет реакций в опорах

Количество и направление реакций зависит как от вида опор, так и от способа нагружения бруса и для статически определимых систем определяются из уравнений равновесия конструкции или ее элементов.

Для общего случая нагружения (пространственных систем), при котором может возникать до 6 реакций опор, требуется соответствующее количество уравнений.

Например, из условия, что заданная система относительно опор не перемещается в пространстве (вправо-влево, вверх-вниз, и вперед-назад) можем приравнять к нулю сумму проекций всех сил на оси x, y и z.

Из условия, что система не вращается, приравниваем к нулю суммы моментов всех нагрузок относительно соответствующих осей.

Совместное решение системы полученных уравнений позволяет определить величину и направление реакций в опорах.

Для плоской системы нагружения можно составить максимум три уравнения равновесия для определения до трех искомых усилий в опорах.

Линейно нагруженные элементы позволяют записать лишь одно уравнение равновесия.

Для расчета реакций опор статически неопределимых систем помимо уравнений статики требуются дополнительные зависимости, связывающие усилия с соответствующими им деформациями.

В некоторых случаях опорные реакции могут быть равны нулю. Это говорит лишь о том, что внешние нагрузки и остальные реакции взаимно уравновешены таким образом, что система может оставаться статичной и без соответствующего усилия в данной точке.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник