Что такое оптимальность конструкции
 |
Согласно принципу соответствия, задача анализа (синтеза) должна решаться в том объеме, в том направлении и на ту глубину, которые соответствуют целям моделирования.
6. Принцип информативности модели.
Вытекает из принципов адекватности и максимального упрощения и предполагает, что в модель закладывается наиболее существенная и значимая информация, она является генератором, существенно значимой информации в смысле ее целевого назначения. И, исходя из принципа информационной прозрачности, вся существенная информация, заложенная и считываемая с модели, доступна эксперту по моделированию.
Модель должна быть информативной, т.е. обладать свойством аккомулирования наиболее существенной, актуальной и полезной информации и одновременно генерировать (порождать) новую информацию с определенными целями и задачами моделирования.
Интерпретация сообщения порождает информацию, следовательно информация и сообщения – различные категории. Сообщение может быть информативным или неинформативным.
Если в модель закладывают информацию, не несущую ничего нового для нас, то она выступает в роли генератора.
Информативность модели состоит в комбинировании и порождении новой информации.
7. Принцип оптимальности конструкции.
Формулировка принципа минимальной (оптимальной) конструкции:
Конструкция модели должна состоять из минимально возможного количества компонент, совокупность которых вещественно, энергетически и информационно оптимальным образом удовлетворяет принципу целенаправленности, т.е. целевому назначению модели.
При исследовании (анализе) сложных объектов выделяются и учитываются наиболее существенные по отношению к преследуемым целям и задачам моделируемые аспекты, свойства, явления – компоненты исследуемой системы и игнорируются малосущественные, второстепенные.
Реализация осуществляется на основе методов стратификации и декомпозиции, а также принципе модульности конструкции (разделяй и властвуй).
8. Принцип максимального упрощения.
При исследовании (анализе) сложных объектов выделяются и учитываются наиболее существенные по отношению к преследуемым целям и задачам моделируемые аспекты, свойства, явления – компоненты исследуемой системы и игнорируются малосущественные, второстепенные.
Реализация ПМУ осуществляется на основе методов стратификации и декомпозиции, а также принципе модульности конструкции (разделяй и властвуй).
9. Принцип интерпретируемости модели.
Модель становится конкретной только в том случае, если она интерпретируема семантически, синтаксически, качественно и количественно в терминах, символах, понятиях,
Принцип интерпретируемости предполагает, что объект интерпретируется по всем уровням анализа, т.е. альтитуды.
Уровни анализа приводят при интерпретации к уровням абстракции или конкретизации, в зависимости от направления движения.
10. Принцип адекватности модели.
Модель и объект-оригинал должны находиться между собой в отношениях адекватности. Адекватность устанавливает не только факт соответствия через интерпретируемость модели в терминах «объекта-оригинала» на семантическом и синтаксическом уровнях, но также качественную близость модели к объекту оригиналу, определяемую в соответствии с целями и задачами моделирования.
В тех случаях, когда смысловая интерпретация объекта и модели совпадают, то говорят, что модель релевантна объекту-оригиналу, либо адекватна в семантическом аспекте.
Чтобы распечатать файл, скачайте его (в формате Word).
Что такое оптимальность конструкции
Выберите два верных ответа из пяти и запишите в таблицу цифры, под которыми они указаны.
По каким принципам организованы биологические системы?
1) закрытость системы
2) высокая энтропия системы
3) низкая упорядочность
4) иерархичность – соподчинение элементов и частей
5) оптимальность конструкции
Одним из принципов организации любой биологической системы является её открытость для веществ, энергии и информации. Раздражимость — это специфические избирательные ответные реакции организмов на изменения окружающей среды. Всякое изменение окружающих организм условий представляет собой по отношению к нему раздражение, а его ответная реакция является проявлением раздражимости. Отвечая на воздействия факторов среды, организмы взаимодействуют с ней и приспосабливаются к ней, что помогает им выжить.
Реакции многоклеточных животных на раздражители, осуществляемые и контролируемые центральной нервной системой, называются рефлексами. Организмы, не имеющие нервной системы, лишены рефлексов, и их реакции выражаются в изменении характера движения (таксисы) или роста (тропизмы).
Представляя собой совокупность взаимосвязанных и взаимодействующих элементов, биологические системы обладают свойствами целостности (несводимость свойств системы к сумме свойств её элементов), относительной устойчивости, а также способностью к адаптации по отношению к внешней среде, развитию, самовоспроизведению и эволюции.
Любая биологическая система является динамической — в ней постоянно протекает множество процессов, часто сильно различающихся во времени. В то же время биологические системы — открытые системы, условием существования которых служит обмен энергией, веществом и информацией как между частями системы (или подсистемами), так и с окружающей средой.
А что такое энтропия?
Энтропия это свойство состояния изолированной (или принимаемой за таковую) физической системы, характеризуемое количеством самопроизвольного изменения, на которое она способна.
Живой организм с точки зрения протекающих в нем физико-химических процессов можно рассматривать как сложную открытую систему, находящуюся в неравновесном, нестационарном состоянии. Для живых организмов характерна сбалансированность процессов обмена, ведущих к уменьшению энтропии. Конечно, с помощью энтропии нельзя охарактеризовать жизнедеятельность в целом, так как жизнь не сводится к простой совокупности физико-химических процессов. Ей свойственны другие сложные процессы саморегуляции.
Топологическая оптимизация геометрии изделия как путь повышения прибыльности предприятия
Если говорить сухим академическим языком, топологическая оптимизация – это процесс изменения конструкции, структуры детали и ее варьирующихся параметров при заданном критерии оптимальности с сохранением или улучшением ее функционала.
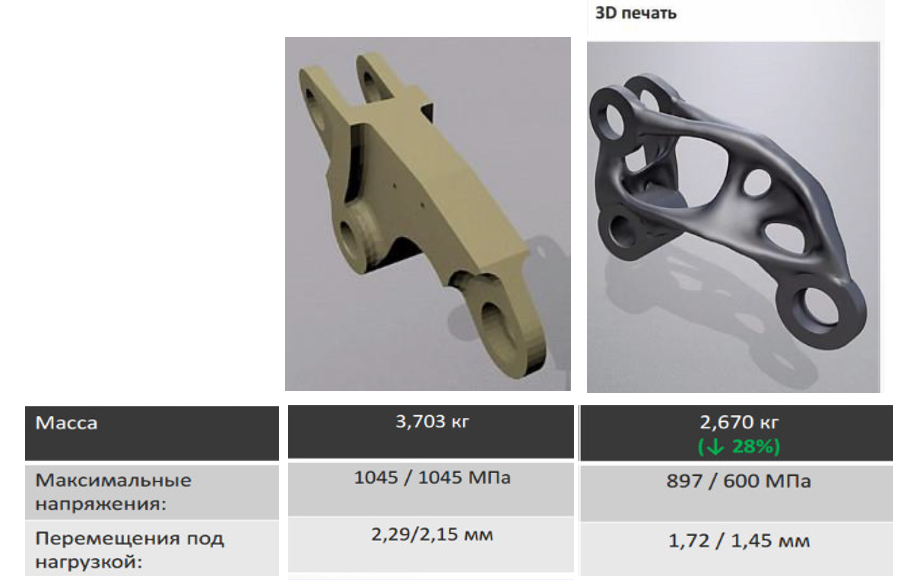
Объясним более доступно на конкретном примере. Возьмем две детали, выполняющие одну и ту же функцию с определенными нагрузками и имеющие определенный ресурс (см. рисунок ниже). По сути, это одна и та же деталь, но с разной геометрией. Геометрия первой детали оптимизирована для изготовления стандартными методами производства: на фрезерном, токарном станке и средствами других технологий металлообработки. Это простая и плоская геометрия, ее легко добиться при обработке на станке. У второй детали геометрия более сложная, и сделать ее на станке представляет серьезные трудности.
Геометрия без ограничений
Когда еще не существовало аддитивных технологий, а были только субтрактивные, то вопрос геометрии не стоял так остро и решался доступными способами. Топологическая оптимизация позволяет изменить стандартную геометрию на геометрию, специально адаптированную под определенную технологию. И это может быть и традиционная технология (например, литье), и аддитивный процесс.
Согласно данным, у второй детали меньше напряжение, меньше перемещение под нагрузкой и, самое главное, вес уменьшился на 1 кг. Для одной детали немного, но если их выпускают сто тысяч в год, то суммарно мы можем сэкономить сто тонн металла только на одной детали.
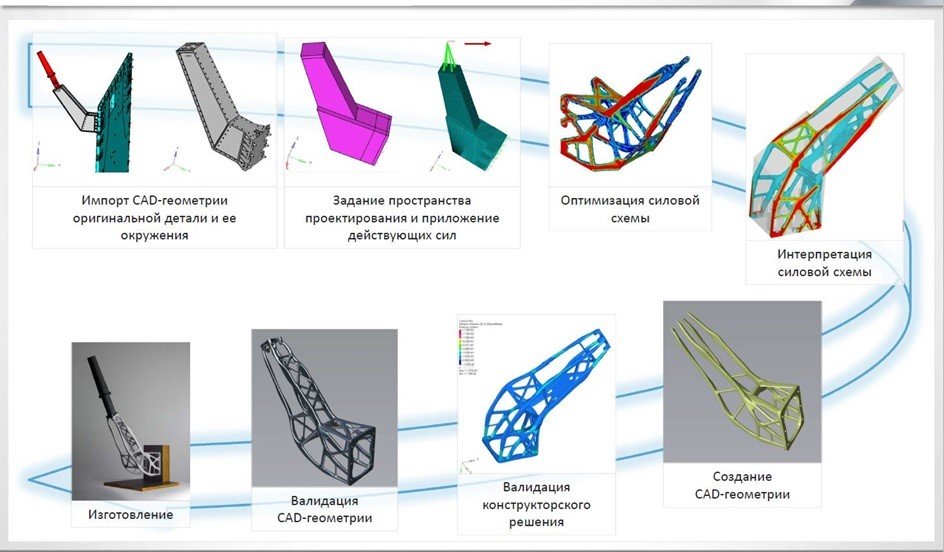
Программное обеспечение для топологической оптимизации не строит модель объекта с нуля. В него загружается геометрическая модель изделия, ранее изготовленного другим методом. На рисунке приведен пример изделия с простыми плоскими формами и заклепками, болтами, приваренными ребрами. Когда мы загрузили модель, мы отмечаем места, которые не полежат изменению. В данном случае это крепления. Все остальное, что не попало в эти зоны, но принадлежит детали, является так называемой design space, то есть той зоной, где программа может менять геометрию.
Затем мы в соответствии со служебным назначением изделия накладываем нагрузки, которые деталь должна выдерживать, то есть создаем силовую схему нагрузок. И далее, на основе заданных нами параметров, программа начинает создавать новую оптимизированную геометрию. Между двумя неизменными местами для крепления она выстраивает новую модель. Она анализирует напряжение в каждом сечении – выдерживает его сечение или нет. Если не выдерживает, то программа меняет сечение.
Процесс построения новой модели довольно затратный по времени и требует больших вычислительных ресурсов. Этот метод моделирования называется методом конечных элементов. Для каждой точки изделия программа составляет и решает интегральные уравнения, учитывая при этом взаимосвязи между всеми точками. В результате расчета получается новая геометрия. Затем конструктор может изменить что-то в модели, если это необходимо. В итоге получается CAD-модель.
Далее для верификации модель загружается в другое программное обеспечение, в котором она проходит финальную проверку на максимальные деформации, напряжения и пр. Затем геометрия утверждается и может быть передана в производство. При этом программа умеет оптимизировать геометрию под разные виды производства: под литье, штамповку, ковку или под аддитивное производство.
Топологическая геометрия, как правило, имеет аморфные формы, в ней нет плоских, прямых линий, могут быть сплайны второго порядка. При соблюдении тех же самых свойств и нагрузочных характеристик такое моделирование позволяет уменьшить массу изделия, и, следовательно, сократить издержки на производство. Понижение массы изделия при сохранении функционала изделия – это задача номер один в самолетостроении, авиакосмической отрасли и автомобилестроении.
Создание ячеистых и сетчатых структур
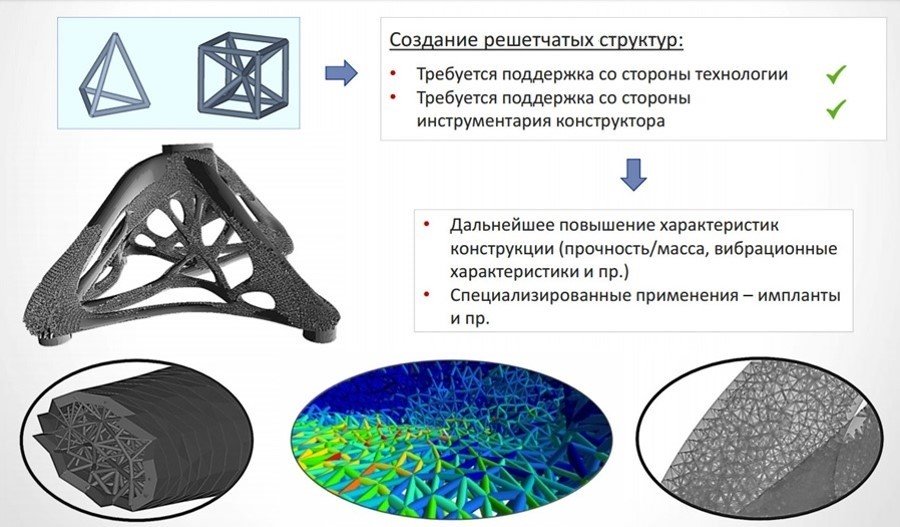
В природе такие структуры встречаются очень часто. Кости птиц могут быть почти пустотелыми, а кость млекопитающих представляет из себя жесткую оболочку с губчатой структурой внутри. Это позволяет выдерживать те же нагрузки при меньших затратах организма на выращивание такой кости и меньшем весе.
Топологическая оптимизация дает возможность делать решетчатые структуры разных форм и размеров (например, гексагоновые) или создавать ячеистую структуру, а снаружи – твердую оболочку. Стандартными методами такую структуру нельзя изготовить – только с использованием аддитивных технологий.
Сокращение числа единиц в сборке
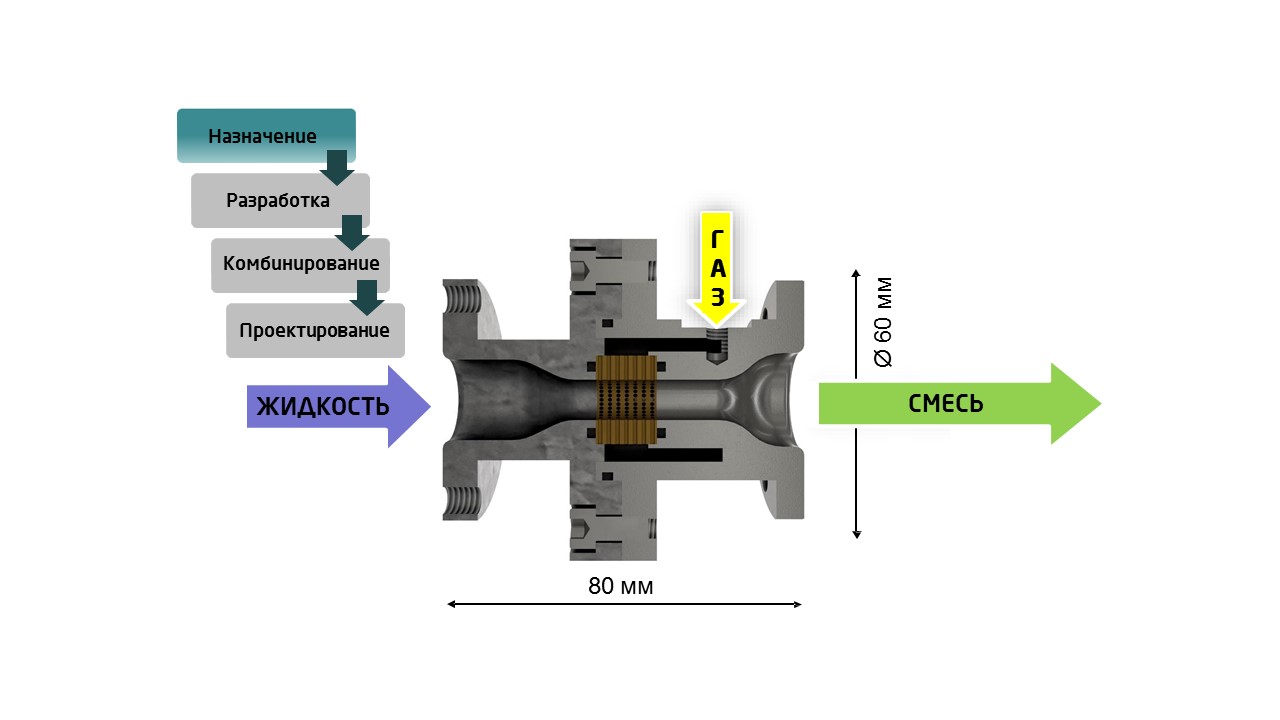
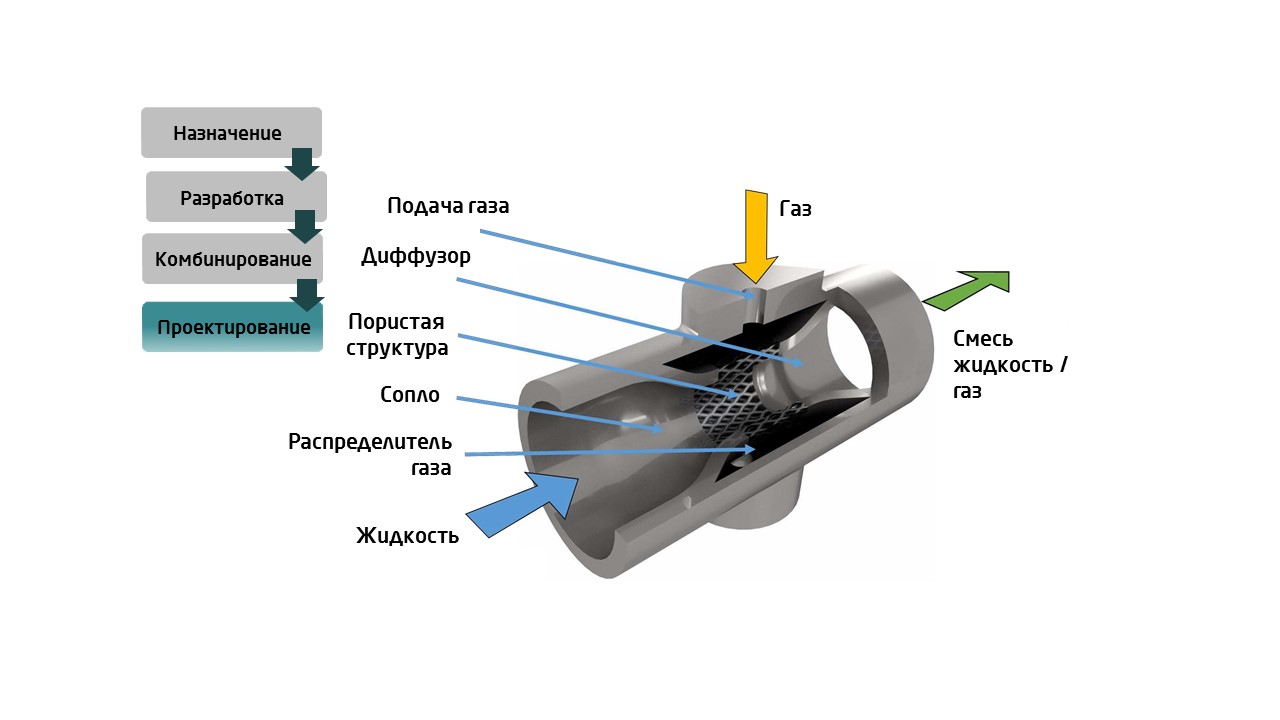
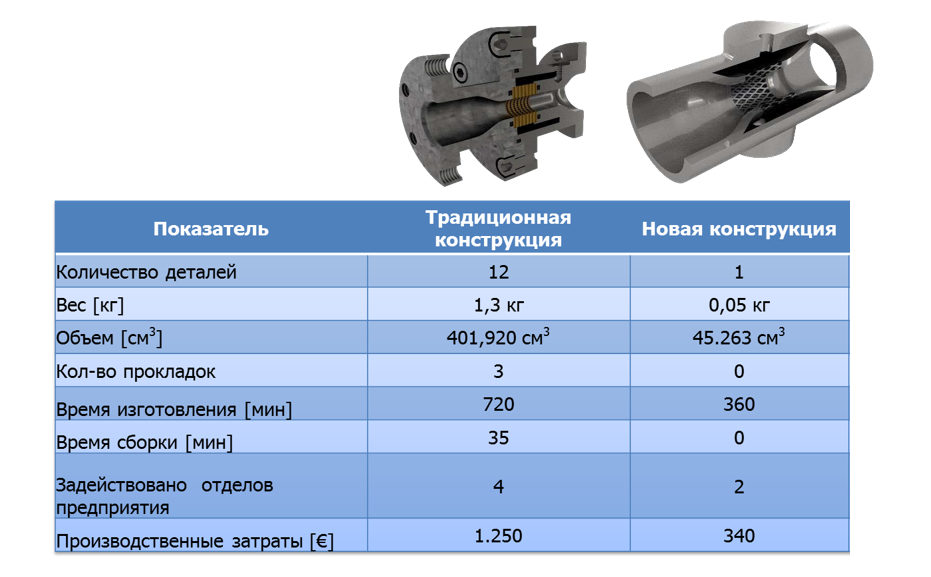
Это еще одно преимущество топологической оптимизации вместе с аддитивными технологиями. Пример: на рисунке изображен типичный сатуратор (смеситель жидкости с газом). Внутри трубы стоит маленький фильтр. Чтобы установить его туда, необходимо эту деталь сделать разъемной в двух частях, сделать фланцы для крепления, а также прокладки, болты и т.д.
С помощью аддитивных технологий можно в одном корпусе создать и саму трубу, и мелкий фильтр внутри, и канал вокруг для распределения газа.
В итоге, применяя 3D-печать металлом, получаем в цельном корпусе единую деталь, одну единицу хранения. Теперь не требуется операция сборки, нет прокладок, которые могут течь, нет больших фланцев, на которые уходил металл.
Если мы уменьшаем вес детали в самолете всего на 200 г, а в нем таких деталей 100, то мы экономим 20 кг, а при ресурсе самолета в 25 лет это огромная экономия топлива или лишняя полезная нагрузка.
Таким образом, топологическая оптимизация – это моделирование в специализированном программном обеспечении, которое позволяет создать геометрию без ограничений.
оптимальная конструкция
оптимальная конструкция
—
[А.С.Гольдберг. Англо-русский энергетический словарь. 2006 г.]
Тематики
Смотреть что такое «оптимальная конструкция» в других словарях:
ГОСТ 20718-75: Катушки индуктивности аппаратуры связи. Термины и определения — Терминология ГОСТ 20718 75: Катушки индуктивности аппаратуры связи. Термины и определения оригинал документа: 71. Базовая конструкция катушки индуктивности Базовая конструкция Е. Unified construction of coil F. Construction normalisée de bobine… … Словарь-справочник терминов нормативно-технической документации
Паровая турбина — первичный паровой двигатель с вращательным движением рабочего органа ротора и непрерывным рабочим процессом; служит для преобразования тепловой энергии пара водяного (См. Пар водяной) в механическую работу. Поток водяного пара поступает… … Большая советская энциклопедия
максимальная — максимальная: Максимально возможная длина ЗО, в пределах которой выполняются требования настоящего стандарта и технических условий (ТУ) на извещатели конкретных типов, Источник: ГОСТ Р 52651 2006: И … Словарь-справочник терминов нормативно-технической документации
ПОЛЕТА ТЕОРИЯ И ПРАКТИКА — совокупность прикладных знаний, позволяющих авиационным инженерам на занятий в области аэродинамики, проблем прочности, двигателестроения и динамики полета летательных аппаратов (т.е. теории) создать новый летательный аппарат или улучшить… … Энциклопедия Кольера
Основы теории и история развития компоновки танка — Введение Современный читатель популярных военно технических изданий избалован обилием материалов по истории создания, боевому применению, особенностям конструкции вооружения и военной техники. Мой опыт общения с фанатами военной техники… … Энциклопедия техники
перегородка (в здании) — перегородка Ненесущая внутренняя вертикальная ограждающая конструкция, разделяющая помещения [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Перегородки являются планировочным элементом, с помощью которого… … Справочник технического переводчика
СТО НОСТРОЙ 2.25.23-2011: Автомобильные дороги. Строительство земляного полотна автомобильных дорог. Часть 1. Механизация земляных работ при сооружении земляного полотна автомобильных дорог — Терминология СТО НОСТРОЙ 2.25.23 2011: Автомобильные дороги. Строительство земляного полотна автомобильных дорог. Часть 1. Механизация земляных работ при сооружении земляного полотна автомобильных дорог: 3.1 влажность : Отношение количества воды… … Словарь-справочник терминов нормативно-технической документации
СП 78.13330.2012: Автомобильные дороги — Терминология СП 78.13330.2012: Автомобильные дороги: 3.1 автомобильная дорога : Комплекс конструктивных элементов, предназначенных для движения с установленными скоростями, нагрузками и габаритами автомобилей и иных наземных транспортных средств … Словарь-справочник терминов нормативно-технической документации
Бесстыковой путь — (или Бархатный) условное наименование железнодорожного пути, расстояние между рельсовыми стыками которого знач … Википедия
Подводные лодки типа U — ПЛ типа «U» U / V class … Википедия
СОДЕРЖАНИЕ
Преимущества
Оптимальные планы имеют три преимущества перед субоптимальными экспериментальными планами :
Минимизация дисперсии оценок
Экспериментальные планы оцениваются с использованием статистических критериев.
Другие критерии оптимальности связаны с дисперсией прогнозов :
Контрасты
Реализация
Каталоги оптимальных проектов встречаются в книгах и в библиотеках программного обеспечения.
Кроме того, в основных статистических системах, таких как SAS и R, есть процедуры для оптимизации проекта в соответствии со спецификациями пользователя. Экспериментатор должен определить модель для плана и критерий оптимальности, прежде чем метод сможет вычислить оптимальный план.
Практические соображения
Некоторые продвинутые темы в оптимальном дизайне требуют больше статистической теории и практических знаний при планировании экспериментов.
Зависимость и надежность модели
Выбор критерия оптимальности и надежности
Выбор подходящего критерия оптимальности требует некоторого размышления, и полезно оценить производительность проектов по нескольким критериям оптимальности. Корнелл пишет, что
Гибкие критерии оптимальности и выпуклый анализ
Высококачественное статистическое программное обеспечение предоставляет комбинацию библиотек оптимальных планов или итерационных методов для построения приблизительно оптимальных планов, в зависимости от указанной модели и критерия оптимальности. Пользователи могут использовать стандартный критерий оптимальности или могут программировать индивидуальный критерий.
Неопределенность модели и байесовские подходы
Выбор модели
Байесовский экспериментальный дизайн
Однако использование байесовского плана не заставляет статистиков использовать байесовские методы для анализа данных. Действительно, некоторые исследователи не одобряют «байесовский» ярлык для вероятностных экспериментальных планов. Альтернативная терминология для «байесовской» оптимальности включает «среднюю» оптимальность или «популяционную» оптимальность.
Итеративное экспериментирование
Последовательный анализ
Методология поверхности отклика
Идентификация системы и стохастическая аппроксимация
Указание количества экспериментальных запусков
Использование компьютера для поиска хорошего дизайна
Дискретные планы измерения вероятности
В математической теории оптимальных экспериментов оптимальный план может быть вероятностной мерой, которая поддерживается в бесконечном множестве точек наблюдения. Такие оптимальные схемы измерения вероятностей решают математическую задачу, в которой не учитывается стоимость наблюдений и экспериментальных прогонов. Тем не менее, такие оптимальные планы с вероятностной мерой могут быть дискретизированы для получения приблизительно оптимальных планов.
История
Логика не возьмется сообщать вам, какие эксперименты вам следует провести, чтобы наилучшим образом определить ускорение свободного падения или величину Ома; но он расскажет вам, как приступить к формированию плана экспериментов.
Кирстин Смит предложила оптимальные планы для полиномиальных моделей в 1918 году (Кирстин Смит была ученицей датского статистика Торвальда Н. Тиле и работала с Карлом Пирсоном в Лондоне).
Смотрите также
Примечания
использованная литература
дальнейшее чтение
Учебники для практиков и студентов
Учебники с упором на методологию регрессии и поверхности отклика
Учебник Аткинсона, Донева и Тобиаса использовался для кратких курсов для промышленных практиков, а также для университетских курсов.
Учебники с упором на блочные конструкции
Оптимальные блочные конструкции обсуждаются Бейли и Бапатом. В первой главе книги Бапата рассматривается линейная алгебра, используемая Бейли (или более сложные книги, приведенные ниже). Упражнения Бейли и обсуждение рандомизации подчеркивают статистические концепции (а не алгебраические вычисления).
Оптимальные блочные конструкции обсуждаются в продвинутой монографии Шаха и Синхи и в обзорных статьях Ченга и Маджумдара.