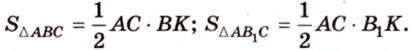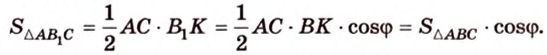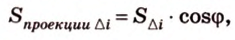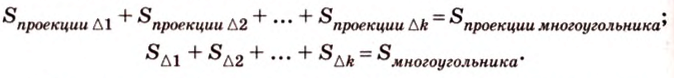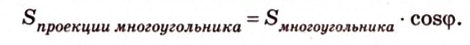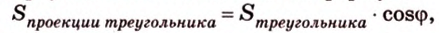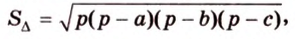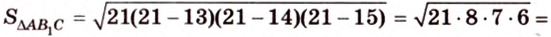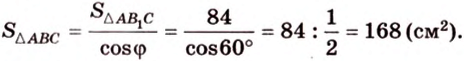Что такое ортогональная проекция вектора
Ортогональная проекция
Резюме
Чертеж ортогональной проекции
Ортогональная проекция в «элементарной» аффинной геометрии
Плоская геометрия
Ортогональная проекция на линию, расстояние
Простейший пример проекции расположен в обычной плоскости (евклидова аффинная): ортогональная проекция на прямую (D) точки A, отмеченная p (D) (A), является точкой H, принадлежащей (D) такой, что линии (D) и (AH) перпендикулярны :
Выражение «опустить перпендикуляр от A» часто используется для построения H, что можно сделать с помощью линейки и циркуля. Аналитически H можно найти, выполнив скалярное произведение:
Общий случай сразу выводится из случая унитарности. Продемонстрируем последнее. v → <\ displaystyle <\ vec 
B ЧАС → знак равно B ЧАС ¯ v → знак равно ( B ЧАС → ⋅ v → ) v → <\ displaystyle <\ overrightarrow <\ mathrm .
Обратите внимание, что у нас есть
Тогда расстояние AH меньше, чем расстояние AM для других точек M из (D), строго за исключением случаев, когда M = H.
Это расстояние называется расстоянием от точки A до линии (D) и часто обозначается d (A, (D)):
Точка A находится на прямой (D) тогда и только тогда, когда она равна своей проекции
или тогда и только тогда, когда его расстояние до (D) равно нулю:
В аналитической геометрии, если отметить
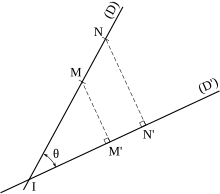
Ортогональная проекция прямой на другую.
Геометрия в космосе
Ортогональная проекция на линию, расстояние
Ортогональная проекция на плоскость, расстояние
Тогда расстояние AH меньше, чем расстояние AM для других точек M от P, строго за исключением случая, когда M = H. Это расстояние называется расстоянием от точки A до плоскости P и часто обозначается d (A, P):
Ортогональная проекция в доильбертовском векторном пространстве
Ортогональная проекция на векторную линию
Икс знак равно Икс F + Икс ⊥ <\ Displaystyle х = х _ <\ mathrm с участием Икс F знак равно ( Икс ⋅ в ) ‖ в ‖ 2 в <\ displaystyle x _ <\ mathrm
Поэтому всегда можно выполнить ортогональную проекцию на векторную линию.
Транзитивность
Наличие ортогональной проекции
Этот пример поразителен: в то время как линия всегда имеет ортогональное дополнение (более того, уникальное), гиперплоскость вполне может не иметь ортогонального дополнения. В такой ситуации сложно нарисовать убедительную картину!
В более общем плане у нас есть эквивалентность следующих свойств:
Попутно это показывает, что ортогональное дополнение, если оно существует, единственно.
Важный случай существования
Общей чертой двух указанных выше достаточных условий является то, что они влекут за собой полноту F (любое конечномерное подпространство предгильберта является полным, а также любое замкнутое подпространство гильберта). На самом деле этого более слабого предположения достаточно:
Минимизация расстояния
Расстояние вектора х на подпространство F есть по определению нижняя грань расстояний от х до всех векторов F:
Характеристики среди проекторов
По подчиненному стандарту
Затем мы можем сформулировать характеристику:
Будучи помощником
Что такое ортогональная проекция вектора
В. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников
.Геометрическое определение вектора
.Алгебраические операции над направленными отрезками
..Сложение направленных отрезков
..Умножение направленных отрезков на число
..Параллельное проектирование вектора в пространстве
..Параллельное проектирование вектора в пространстве
. Проекция точки на плоскость
. Проекция вектора на плоскость
..Ортогональная проекция вектора в пространстве
. Ортогональная проекция вектора на плоскость
. Ортогональная проекция вектора на прямую и направленную ось
..Векторы в трехмерном геометрическом пространстве
..Линейная зависимость векторов и размерность пространства
..Различные формы записи векторов
..Линейные операции над векторами в координатной форме
. Свойства скалярного умножения
. Скалярное умножение в декартовых координатах
..Некоторые примеры использования скалярного умножения
..Площадь параллелограмма, построенного на векторах
..Задачи на применение определителей
..Определитель третьего порядка и его свойства
..Векторное умножение векторов базиса декартовой системы координат
.Ковариантные и контравариантные координаты вектора
..Индексная форма записи для выражений с определителями
..Свойства символов Веблена
..Операция векторного умножения в произвольных косоугольных координатах
.Линейный оператор и его матрица
.Доказательство теоремы об определителе
.Общие определения алгебраических операций с тензорами
.Примеры на применение тензоров в физике
..Задачи на тождественные преобразования
..Параллельное проектирование вектора в пространстве
Проекция точки на плоскость
Проецирование точки на плоскость производится способом аналогичным проецированию точки на прямую в плоскости. Проекцией 
точки A на плоскость α в направлении вектора 
называется точка пересечения плоскости и прямой, проведенной через эту точку в направлении проецирования (рис. 7, а).
а) 
б) 
Рис. 7
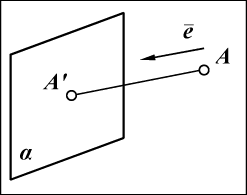
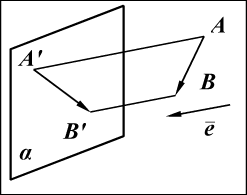
Проекция вектора на плоскость
Проекцией вектора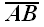 
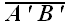
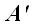
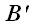
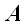
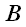
на плоскость α называется вектор 
(рис. 7, б), где точки и 
являются проекциями точек 
и 
соответственно.
Проекция вектора на прямую
Спроектировать вектор на прямую в пространстве аналогично тому, как это можно сделать на плоскости, нельзя.
Рис. 8
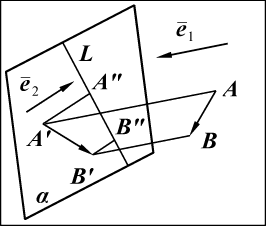
Следовательно, можно дать следующее определение проекции вектора на прямую в пространстве.
Проекцией вектора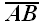 
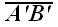
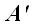
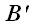
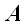
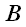
на прямую L по направлению проецирующей плоскости α называется вектор, 
. Точки и при этом являются точками пересечения прямой L и плоскостей, проведенных через точки и параллельно проецирующей плоскости.
Для обозначения проекции вектора на прямую будем использовать следующее обозначение: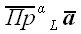 
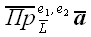
или 
.
Проекция вектора на прямую – величина векторная. Совершенно аналогично тому, что мы имели на плоскости, и для пространственного случая мы можем ввести понятие алгебраического значения проекции вектора на направленную ось. Для обозначения алгебраического значения проекции мы будем (так же как и в «плоском» случае) использовать то же самое обозначение, только без «векторной» черты сверху: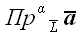 
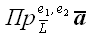
или 
. И, что очень приятно, теорема (1), которую мы доказали для «плоского» случая, справедлива и для обеих проекций в пространстве:
1. 
;
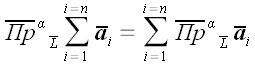
2. 
.
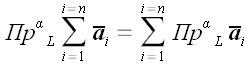
Доказательство полностью аналогично тому, что мы привели для случая на плоскости.
..Ортогональная проекция вектора в пространстве
О ртогональная проекция есть частный случай параллельной проекции и, поэтому для нее справедливы те общие результаты, которые мы уже получили. В то же время ортогональная проекция обладает рядом геометрических свойств, которые выгодно отличают ее от других видов проекции. Физика также имеет свой собственный интерес к этому виду проекции. Например, работа силового поля зависит именно от ортогональной проекции силы на направление перемещения. Можно, видимо, утверждать, что ортогональная проекция и, связанная с ней, ортогональная система координат, о которой мы будем говорить в дальнейшем, выделена самой природой.
Ортогональная проекция вектора на плоскость
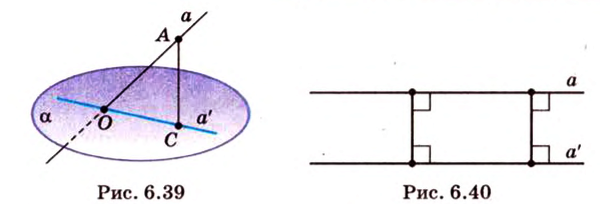
Ортогональную проекцию мы получим, если вектор, задающий направление проектирования, ортогонален плоскости, на которую производится проектирование. Поскольку при ортогональном проектировании направление проектирования задается однозначно самой плоскостью, то в условном обозначении его можно опустить: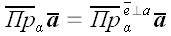 
.
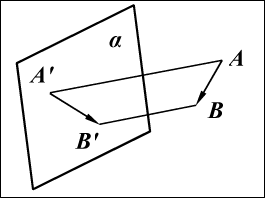
Рис. 9
Для получения ортогональной проекции вектора на плоскость достаточно из начала и конца вектора опустить на эту плоскость перпендикуляры. Основания этих перпендикуляров и определяют проекцию вектора на плоскость (рис. 9):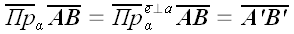 
.
Ортогональная проекция вектора на прямую и направленную ось
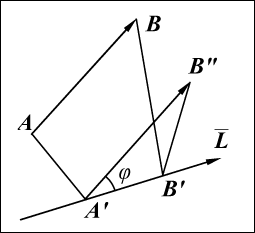
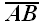
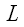
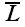
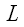
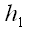
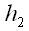
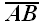
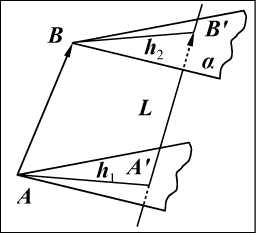
Для построения ортогональной проекции вектора на прямую 
или ось 
необходимо использовать проектирующую плоскость α ортогональную прямой, либо просто опустить на прямую перпендикуляры (
, 
) из начала и конца вектора (рис 10).
Рис. 10
В условных обозначениях это запишется так:
; и для алгебраической величины ортогональной проекции вектора на направленную ось – 
, где s – знак плюс или минус.
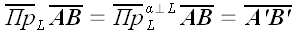
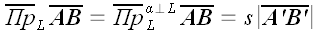
Теперь придется сказать несколько слов об употреблении термина «проекция». Мы уже ввели несколько понятий, каждое из которых претендует на это название: проекция вектора на плоскость, «векторная» проекция вектора на прямую, алгебраическое значение проекции вектора на направленную ось, ортогональная проекция вектора на плоскость, «векторная» ортогональная проекция вектора на прямую и алгебраическое значение ортогональной проекции вектора на направленную ось. Наиболее длинным и неудобным по названию и одновременно наиболее часто используемым является последнее понятие. В силу этого название «проекция» в векторной алгебре закрепилось именно за алгебраическим значением ортогональной проекции вектора на направленную ось. В дальнейшем мы также не будем отступать от этой традиции, тем более что из контекста обычно всегда ясно, о чем идет речь.
Итак, проекцией вектора на направленную ось будем называть алгебраическое значение его ортогональной проекции на эту ось.
Мы не будем считать это определением проекции вектора на направленную ось, а лишь удобным соглашением о названии.
Свойства ортогональной проекции вектора на направленную ось.
1. Проекция суммы векторов равна сумме их проекций.
;
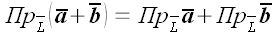
и для любого их количества
.
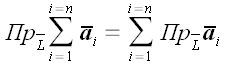
2. Проекция произведения вектора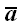 
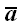
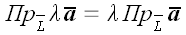
на действительное число λ равна произведению числа λ на проекцию вектора .
.
Если первые два свойства справедливы для всех типов проекций, и мы их сформулировали более для порядка, то следующее свойство является «визитной карточкой» ортогональной проекции.
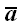
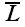
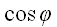
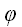
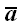
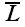
3. Проекция вектора на направленную ось равна произведению его модуля на 
, где угол 
– угол между вектором и направленной осью (рис. 11). Дадим этому свойству доказательство.
Рис. 11
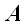
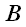
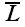
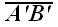
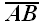
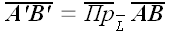
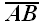
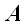
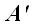
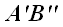
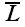
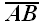
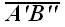
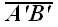
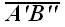
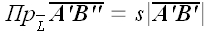
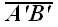
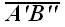
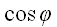
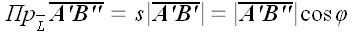
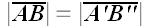
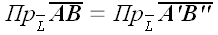
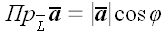
Спроектируем точки и (конечно, ортогонально) на прямую . Вектор есть проекция вектора : 
. Перенесем вектор параллельно самому себе так, чтобы точка совпала с точкой . Минимальный угол между векторами 
и принимается за угол принимается за угол φ между вектором и осью. Поскольку равные векторы имеют и равные проекции, то проекции векторов и 
одинаковы и равны 
. Алгебраическая величина проекции вектора , или просто проекция, в соответствии с соглашением о названиях, равна 
, где s означает знак «плюс» или «минус». А модуль вектора , в свою очередь, равен произведению модуля вектора на :
.
и
, получаем окончательно 
.
Ортогональное проецирование:
Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.
Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой 
Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.
Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.
Площадь ортогональной проекции
Теорема 5
Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.
Как пример многоугольника возьмем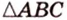 
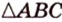
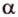
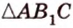
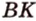
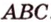
(рис. 6.41). Проекцией 
на плоскость 
является 
. Проведем высоту 
треугольника 
. По теореме
о трех перпендикулярах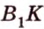 
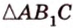
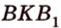
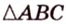
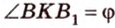
— высота 
. Угол 
— угол между плоскостью 
и плоскостью проекции. Пусть 
. Тогда
Учитывая, что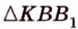 
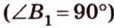
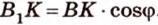
прямоугольный 
, имеем:
. Поэтому
Итак, 
. Теорема доказана.
Чтобы доказать теорему для произвольного многоугольника, его разбивают на треугольники. Тогда для каждого треугольника и его проекции можно записать равенство
где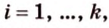 
поскольку угол между плоскостями этих треугольников и плоскостью их проекций будет один и тот же. Все эти равенства сложим почленно:
Т.е. и для этого случая теорема истинна.
Пример:
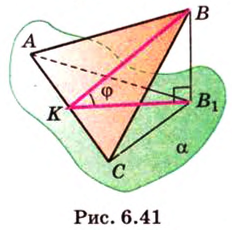
Ортогональной проекцией треугольника является треугольник со сторонами 13 см, 14 см и 15 см. Плоскость треугольника образует с плоскостью проекции угол 60°. Вычислите площадь данного треугольника.
Воспользуемся рисунком 6.41. Известно, что площадь проекции треугольника вычисляют по формуле:
где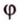 
— угол между плоскостью треугольника и плоскостью проекции.
По формуле Герона найдем площадь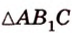 
:
где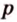 
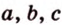
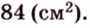
— полупериметр треугольника, 
— его стороны. 
Тогда 
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.