Что такое ортогональное проектирование
Что такое ортогональное проектирование
Мы постоянно встречаемся с различными способами проектирования (или, как еще говорят, проецирования) как в математике, так и в быту: оно применяется при изображении пространственных фигур на плоскости, в частности, при фотографировании и в кино; тени от предметов являются их проекциями; на проектировании основано введение координат как на плоскости, так и в пространстве, изготовление чертежей, планов и т.д. Об одном из способов проектирования — параллельном проектировании — уже говорилось в п. 1.9. Сейчас мы рассмотрим самый простой, но наиболее важный из способов проектирования в пространстве — ортогональное проектирование «ортогональный” в переводе и значит — «прямоугольный»). В этом пункте мы будем говорить просто о проектировании, имея в виду ортогональное проектирование.
О проекции точки и проекции наклонной на плоскость уже говорилось в п. 2.1.
Проекцией же фигуры F на плоскость а называется фигура F, состоящая из проекций всех точек фигуры F на эту плоскость а (рис. 2.32).
Преобразование фигуры F, сопоставляющее каждой точке X фигуры F ее проекцию 
называется проектированием (или проецированием) фигуры F на
Поскольку все прямые, перпендикулярные к одной плоскости, параллельны друг другу, то ортогональное проектирование 
на плоскость является частным случаем параллельного проектирования и обладает всеми свойствами параллельного проектирования.
Кроме точек и отрезков, рисуя изображения сферы, цилиндра или конуса, мы будем встречаться с проекцией окружности на плоскость (когда плоскость окружности не перпендикулярна и не параллельна плоскости проекции). Кривая, которая является проекцией окружности в этом случае, называется эллипсом (рис. 2.33). Эллипсом является и параллельная проекция окружности на плоскость (если направление проектирования не параллельно плоскости окружности). Окружность является частным случаем эллипса. Эллипсы обладают многими замечательными свойствами. Эллипс имеет центр симметрии и две взаимно перпендикулярные оси симметрии. По эллипсам (эллиптическим орбитам) двигаются планеты вокруг Солнца. Солнце, однако, находится не в центре эллипса — орбиты планеты, а в точке, называемой фокусом эллипса.
Ортогональное проектирование на одну, две и три плоскости широко используется в технике, в черчении. Изображение предмета в проекциях позволяет судить о его устройстве, без чего часто невозможно ни конструирование предмета, ни его изготовление.
В дальнейшем, говоря «проекция» или «проектирование», мы имеем в виду ортогональное проектирование и ортогональную проекцию, если нет специальных оговорок.
На ортогональном проектировании основан такой важный для инженеров раздел прикладной математики, как начертательная геометрия. Начертательная геометрия была создана знаменитым французским математиком Гаспаром Монжем (1746—1818). В ее основе лежит идея о том, что положение любой точки пространства
можно задать ее ортогональными проекциями на две взаимно перпендикулярные плоскости 
(рис. 2.34).
Повернем плоскость а, вокруг прямой x пересечения плоскостей 
в направлении, указанном на рисунке 2. 34, до совпадения с плоскостью 
После такого поворота обе плоскости изобразятся на одном и том же чертеже, называемом эпюром (рис. 2.35).
Прямая X называется осью проекции. Плоскости а, и 
разбивают все пространство на четыре четверти — квадранта. В зависимости от того, в каком квадранте лежит точка А, изображения ее проекций 
на эпюре находятся выше или ниже оси проекции (рис. 2.36), причем всегда отрезок 
перпендикулярен прямой x.
Ясно, что если на эпюре заданы изображения 
проекций точки А, то они однозначно определяют положение точки А в пространстве.
Тем самым метод Монжа дает возможность строить эпюр по данной фигуре и, наоборот, восстановить фигуру по ее изображению на эпюре. Сам Монж так определял предмет начертательной геометрии:
Начертательная геометрия преследует две цели: во-первых, дать методы для изображения на листе чертежа, имеющего только два измерения, а именно длину и ширину, любых тел природы, имеющих три измерения — длину, ширину и высоту, при условии, однако, что эти тела могут быть точно заданы.
Во-вторых, дать способ на основании точного изображения определять формы тел и выводить все закономерности, вытекающие из их формы и взаимного расположения.
Г. Монж был не только геометром, но и общественным деятелем в период французской буржуазной революции. Он был морским министром и организатором национальной обороны, одним из создателей Политехнической школы в Париже.
ОСНОВНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
КУРС ЛЕКЦИЙ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
ЛЕКЦИЯ 1
Начертательная геометрия – наука о методах построения изображений различных предметов расположенных в пространстве. Как правило, это делается методом перпендикулярного (ортогонального) проектирования этих предметов на плоскостях проекций, т.е. все проецирующие лучи перпендикулярны плоскостям проекций.
ОСНОВНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
1.Проекция любой точки пространства – единственная точка на плоскости проекций.
Например, точка А проецируется на горизонтальную плоскость 
проекцией А¢¢; если точка М лежит на плоскости , то её проекция М¢ совпадает с М : М 
М¢ (рис. 1).
Точки, лежащие на одной и той же проецирующей прямой, называют конкурирующими. Проекции конкурирующих точек совпадают. На рис. 2 показаны конкурирующие точки К и L и их совпадающие проекции: 
2. Проекция прямой в общем случае – единственная прямая на плоскости проекции.
3.Если точка С принадлежит прямой d(АВ) в пространстве, то проекция 
этой точки на плоскости проекции принадлежит проекции прямой d¢(А¢В¢), т.е. если С 
АВ, то С¢ А¢ В¢ (рис. 3).
4.Если отрезок EF параллелен плоскости проекций, то он проецируется в натуральную величину: 
(рис. 4).
5.Если прямые в пространстве параллельны друг другу, то их проекции также параллельны между собой, т.е. если АВ||CD, то А¢ В¢ ||C¢ D¢ (рис. 5).
6.Если отрезки в пространстве параллельны друг другу, то отношение их длин сохраняется при проецировании, т.е. если АВ||CD, то АВ/CD = А¢ В¢ / C¢ D¢ (рис. 5).
7. Натуральная длина отрезка АВ в пространстве равна длине гипотенузе прямоугольного треугольника, у которого один катет равен проекции отрезка, а второй – превышение одного конца отрезка над другим.Действительно, пусть имеем в пространстве отрезок АВ (рис. 6). Проведем в проецирующей плоскости АВВ¢А¢ прямую АМ || А¢В¢. В результате получим прямоугольный треугольник АВМ, у которого D=ВМ превышение одного конца отрезка АВ над другим, а 
= 
ВАМ – угол наклона отрезка АВ к плоскости .
8.Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то этот прямой угол проецируется на неё в натуральную величину. Например, если 
и АВ|| , то 
(рис. 7).
9. Проекции фигуры АВС – 
и 
не меняются при параллельном переносе плоскости проекций (рис. 8).
ТОЧКА
При рассмотрении свойств ортогонального проектирования видно, что проекции фигур, заданные только на плоскости , не определяют однозначно свои оригиналы в пространстве, поэтому применяется комплексный чертёж, который состоит из двух и более связанных между собой ортогональных проекций предмета. Эти проекции получают на взаимно перпендикулярных плоскостях проекций ( 
и 
), которые совмещаются с плоскостью чертежа. Плоскость называется горизонтальной, а – фронтальной (вертикальной) плоскостью проекций. Линии пересечения этих плоскостей называются осями проекций (х, у, z).
Каждый предмет можно рассматривать как совокупность точек. Таким образом, изучение метода ортогональных проекций начинается с изучения проецирования точки.
Любая точка пространства (например, точка А на рис. 1) проецируется ортогонально на плоскости 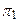и , образуя свои горизонтальную 
и фронтальную 
проекции.
Можно строить проекции также на плоскости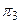 
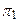
, перпендикулярной и . Она носит название профильной плоскости проекций: 
– профильная проекция точки А.
Важно отметить, что проекции отрезков каждой проецирующей прямой равны между собой: 
(аппликата);
(ордината);
(абсцисса).
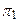
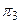
Для образования плоского чертежа плоскость проекций путем вращения вокруг оси х совмещают с плоскостью , а плоскость проекций совмещается с плоскостью путем вращения вокруг оси z. Полученный таким образом плоский комплексный чертеж содержит три проекции точки А, причем как видно из рис. 2, каждая пара смежных проекций ( и ; и ) лежит на одной прямой, перпендикулярной соответствующей оси. Такая прямая называется линией связи.
Рис. 3
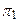
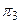
В объёмном отображении три взаимно перпендикулярные плоскости проекций , и являются неограниченными поверхностями и при взаимном пересечении делят все пространство на восемь прямых трехгранных угла (восемь октантов) (Рис. 3).
ПРЯМАЯ
Прямая на ортогональном чертеже может быть задана проекциями пары точек.
На рис. 4.1. показана пространственная модель, а на рис. 4.2. – комплексный (ортогональный) чертеж прямой АВ.
Проекции точек А и В определяют единственную прямую пространства. Для построения профильной проекции можно использовать разность профильных координат точек А и В, равную 
(рис. 4.2.).
Точка К принадлежит прямой, если обе её проекции 
и 
принадлежат соответствующим проекциям этой прямой (рис. 4.2.).
Точки пересечения прямой с плоскостями проекций называют следами.
На рис. 4.1. показаны точки М и N, в которых прямая, заданная отрезком АВ, пересекает плоскости проекций. Точка М – горизонтальный след прямой, а точка N – фронтальный след.
Горизонтальная проекция горизонтального следа 
совпадает с самим следом, а фронтальная проекция этого следа 
лежит на оси проекций. Фронтальная проекция фронтального следа 
совпадает с точкой N, а горизонтальная проекция 
лежит на оси проекций.
Следовательно, чтобы найти горизонтальный след, надо продолжить фронтальную проекцию 
до пересечения с осью х и через точку (фронтальная проекция горизонтального следа) провести перпендикуляр к оси х до пересечения с продолжением горизонтальной проекции 
.
Точка – горизонтальная проекция горизонтального следа, она совпадает с самим следом.
Для нахождения фронтального следа продолжим горизонтальную проекцию до пересечения с осью х, через точку (горизонтальную проекцию фронтального следа) проводим перпендикуляр до пересечения с продолжением фронтальной проекции . Точка – фронтальная проекция фронтального следа, она совпадает с самим следом.
Линии нулевого уровня лежат в плоскостях проекций. Проекции этих линий лежат в плоскостях проекций.
Прямая не имеет следа на плоскости проекций в том случае, когда она параллельна этой плоскости.
Прямые, не перпендикулярные и не параллельные плоскостям проекций, называют прямыми общего положения.
Линии, параллельные плоскостям проекций, называют линиями уровня.
Если прямая параллельна горизонтальной плоскости проекций, её называют горизонталью, фронтальной – фронталью, профильной – профильной прямой. Обозначают их соответственно буквами h, f и р.
Отрезок линии уровня в соответствии со свойством 4 проецируется на параллельную ему плоскость проекций в натуральную величину.
Часто бывает необходимо построить перпендикуляр к прямой уровня.
Рассмотрим пример. Пусть задана фронталь f (рис. 4.2 а). Требуется из точки А опустить на фронталь перпендикуляр n.
На основании свойства 8 ортогонального проецирования прямой угол проецируется без искажения, если одна из его сторон – линия уровня.. Следовательно, прямой угол между f и n проецируется на в натуральную величину: 
, так как 
параллельна . Точка 
– основание перпендикуляра. Горизонтальная проекция перпендикуляра 
определяется положением точек 
и .
Аналогично строится перпендикуляр m к горизонтали h (рис. 4.2 б).
Проецирующие прямые (прямые, перпендикулярные одной из плоскостей проекций) также являются линиями уровня. Причем одна из её проекций вырождается в точку (рис. 14.1.).
Конкурирующие точки, лежащие на одной проецирующей прямой, дают возможность определить видимость отдельных элементов предмета на данной плоскости проекций. Из двух горизонтально конкурирующих точек К и М (рис. 14.1.) на плоскости видима та, которая расположена выше, т.е. К. Из двух фронтально конкурирующих точек L и N на плоскости видима та, которая ближе к наблюдателю, т.е. L, а точка N невидима, так как расположена за точкой L.