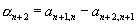Что такое ортогональность в дискретной математике

Ортогональные многочлены

Полезное

Смотреть что такое «Ортогональные многочлены» в других словарях:

ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ — система многочленов <Р n (х)>, удовлетворяющих условию ортогональности причем степень каждого многочлена Р n (х). равна его индексу п, а весовая функция (вес) на интервале ( а, b).или (в случае конечности a и b) на отрезке [a, b]. О. м. наз. о р… … Математическая энциклопедия

Ортогональные многочлены — Пафнутий Львович Чебышёв В математике последовательностью ортогональных многочленов называют бесконечную последовательность действительных многочленов … Википедия

ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ — в комплексной области общее название многочленов, ортогональных на окружности, по контуру или по площади. В отличие от случая ортогональности в действительной области, многочлены указанных трех систем могут иметь мнимые коэффициенты и… … Математическая энциклопедия

КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ — общее название Якоби многочленов, Эрмита многочленов, Лагерра многочленов и Чебышева многочленов. Эти системы ортогональных многочленов обладают общими свойствами: 1) Весовая функция j(х)на интервале ортогональности ( а, b )удовлетворяет… … Математическая энциклопедия

Многочлены Эрмита — Многочлены Эрмита определённого вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1… … Википедия

Многочлены Чебышёва — две последовательности многочленов Tn(x) и Un(x), названные в честь Пафнутия Львовича Чебышёва. Многочлены Чебышёва играют важную роль в теории приближений, поскольку корни многочленов Чебышёва первого рода используются в качестве узлов в… … Википедия

Многочлены Якоби — Полиномы Якоби класс ортогональных полиномов. Названы в честь Карла Густава Якоба Якоби. Ортогональные полиномы Якоби Открыты Якоби, Карл Густав Якоб Формула … Википедия

Источник

Основы дискретной математики

Привет, хабр. В преддверии старта базового курса «Математика для Data Science» делимся с вами переводом еще одного полезного материала.

Об этой статье

Эта статья содержит лишь малую часть информации по заявленной теме. Рассматривайте ее как вводный курс перед началом всестороннего изучения предмета. Надеюсь, вы найдете в ней полезную информацию. Знание дискретной математики помогает описывать объекты и задачи в информатике, особенно когда дело касается алгоритмов, языков программирования, баз данных и криптографии. В дальнейшем я планирую подробнее раскрыть темы, затронутые в этой статье. Приятного чтения!

ЧТО ТАКОЕ ДИСКРЕТНАЯ МАТЕМАТИКА?

Это область математики, изучающая объекты, которые могут принимать только уникальные отдельные значения.

Мы рассмотрим пять основных разделов в следующем порядке.

ЛОГИКА

Что такое логика?

Это наука о корректных рассуждениях. Мы будем использовать приемы идеализации и формализации. Неформальная логика изучает использование аргументов в естественном языке.

Формальная логика анализирует выводы с чисто формальным содержанием. Примерами формальной логики являются символическая логика и силлогистическая логика (о которой писал Аристотель).

Начнем с азов. Рассмотрим следующее высказывание на естественном языке:

«Если я голоден, я ем».

Пусть «голоден» будет посылкой A, а «ем» — следствием B. Попробуем формализовать:

A => B (то есть из A следует B)

NB. Посылка и следствие являются суждениями.

Логические выражения

Для нас важна форма, а НЕ содержание. Значение будет истинным, если оно соответствует форме.

Например, 10 4 — ИСТИНА.

Логические операции

Суждение P — это утверждение, которое может быть как истинным, так и ложным.

Обозначим истинное значение P единицей (1), а ложное значение P нулем (0).

Существует другое суждение; обозначим истинное значение Q единицей (1), а ложное значение Q нулем (0).

Рассмотрим логические операции с суждениями, значение которых истинно. Они могут сами образовывать истинные значения путем выполнения соответствующих операций над истинными значениями.

Источник

ДИСКРЕТНЫЕ ОРТОГОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ

Линейное преобразование может быть записано как векторно-матричная процедура:

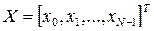
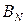
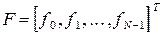
где — вектор исходных данных; — квадратная матрица размера N x N ядра преобразования; — вектор результатов.

Однако обратная матрица может быть определена лишь в том случае, если det[B] отличен от нуля.

Методы дискретных ортогональных преобразований в настоящее время широко используются при обработке сигналов. В таблице 6.1 приведены основные области применения спектральных методов и задачи, решаемые с их помощью [11].

Источник

Ортогональные системы функций. Ряды Фурье по ортогональным системам.

Ортогональные системы функций.

Например, тригонометрическая система
$$
\frac<1><2>,\quad \cos \frac<\pi x>,\quad \sin \frac<\pi x>,\quad \ldots,\quad \cos \frac,\quad \sin \frac, \ldots\label
$$
ортогональна на отрезке \([-l, l]\) (ранее мы уже разбирали этот пример).

Так как
$$
2\int\limits_<-l>^ \left(\frac<1><2>\right)^ <2>dx = \int\limits_<-l>^ \cos^ <2>\frac = \int\limits_<-l>^ \sin^ <2>\frac = l,\ n \in \mathbb,\label
$$
то, поделив все функции тригонометрической системы \eqref на \(\sqrt\), а первую из этих функций на \(\sqrt\), получим ортонормированную на отрезке \([-l, l]\) тригонометрическую систему
$$
\frac<1><\sqrt<2l>>,\quad \frac<1><\sqrt> \cos \frac<\pi x>,\quad \frac<1><\sqrt> \sin \frac<\pi x>, \ldots\label
$$

При \(l = \pi\) тригонометрическая система \eqref имеет особенно простой вид
$$
\frac<1><2>,\quad \cos x,\quad \sin x,\quad \ldots,\quad \cos nx,\quad \sin nx,\quad \ldots\label
$$
и ортогональна на отрезке \([-\pi, \pi]\).

Многочлены Лежандра
$$
L_(x) = \frac<1><2^n!> \frac>>(x^<2>-1)^,\quad n \in \mathbb,\quad L_<0>(x) = 1,\label
$$
образуют ортогональную систему функций на отрезке [—1,1].

\(\vartriangle\) Доказательство ортогональности многочленов Лежандра на отрезке [—1,1] сводится к проверке при \(n > m\) тождества
$$
J = \int\limits_<-1>^ <1>\frac>>(x^<2>-1)^ \frac>>(x^<2>-1)^ dx = 0.\nonumber
$$

Ряд Фурье по ортогональной системе.

Пусть функция \(f(x)\) непрерывна на отрезке \([a, b]\), а \(\<\varphi_(x)\>\) — ортогональная на \([a, b]\) система непрерывных функций, причем ни одна из функций \(\varphi_(x)\) не обращается тождественно в нуль на отрезке \([a, b]\).

Говорят, что функция \(f(x)\) разложена на отрезке \([a, b]\) в сходящийся ряд по ортогональной системе функций \(\<\varphi_(x)\>\), если найдется такая числовая последовательность \(\\>\), что функциональный ряд \(\sum_^ <\infty>a_\varphi_(x)\) сходится и его сумма равна \(f(x)\), то есть
$$
f(x) = \sum_^ <\infty>a_\varphi_(x),\quad x \in [a, b].\label
$$

Если функциональный ряд \eqref сходится равномерно на отрезке \([a, b]\), то справедливы следующие выражения для коэффициентов этого ряда:
$$
a_ = \dfrac<\displaystyle \int\limits_^ f(x)\varphi_(x) dx><\displaystyle\int\limits_^ \varphi_^<2>(x) dx>,\ n \in \mathbb.\label
$$

\(\circ\) Так как функция \(\varphi_(x)\) непрерывна на отрезке \([a, b]\), то она ограничена на этом отрезке (теорема Вейерштрасса). Если равномерно сходящийся ряд умножить на ограниченную функцию, то получим равномерно сходящийся ряд (это непосредственно следует из определения равномерной сходимости функционального ряда). Поэтому, умножая ряд \eqref на функцию \(\varphi_(x)\), получаем
$$
f(x)\varphi_(x) = \sum_^ <\infty>a_\varphi_(x)\varphi_(x),\ n \in \mathbb,\label
$$
причем ряд в правой части равенства \eqref сходится равномерно на отрезке \([a, b]\).

Числа \(a_\) называются коэффициентами Фурье, а ряд \eqref — рядом Фурье функции \(f(x)\) по ортогональной на \([a, b]\) системе функций \(\<\varphi_(x)\>\).

Ряд Фурье функции \(f(x)\) по тригонометрической системе на отрезке \([-l, l]\) будем записывать в виде
$$
f(x) = \frac> <2>+ \sum_^ <\infty>\left(a_ \cos \frac + b_ \sin \frac\right)\label
$$
и называть тригонометрическим рядом Фурье функции \(f(x)\) на отрезке \([-l, l]\).

Коэффициенты \(a_\) и \(b_\) можно вычислить, если подставить в формулы \eqref выражения для тригонометрических функций и воспользоваться формулами \eqref:
$$
a_ <0>= \frac<1> \int\limits_<-l>^ f(x)\ dx,\quad a_ = \frac<1> \int\limits_<-l>^ f(x) \cos \frac\ dx,\\ b_ = \frac<1> \int\limits_<-l>^ f(x) \sin \frac\ dx,\ n \in \mathbb.\label
$$
В частности, при \(l = \pi\) получаем
$$
a_ <0>= \frac<1> <\pi>\int\limits_<-\pi>^ <\pi>f(x)\ dx,\quad a_ = \frac<1> <\pi>\int\limits_<-\pi>^ <\pi>f(x) \cos nx\ dx,\\b_ = \frac<1> <\pi>\int\limits_<-\pi>^ <\pi>f(x) \sin nx\ dx,\ n \in \mathbb.\label
$$

Ряд Фурье абсолютно интегрируемой функции.

Коэффициенты Фурье могут быть вычислены при помощи формулы \eqref для любой абсолютно интегрируемой на отрезке \([a, b]\) функции \(f(x)\), если функции \(\varphi_(x)\) непрерывны и не обращаются тождественно в нуль на отрезке \([a, b]\).

Ряд \(\displaystyle\sum_^ <\infty>a_\varphi_(x)\), где \(a_\) — коэффициенты Фурье абсолютно интегрируемой на \([a, b]\) функции \(f(x)\), будем называть рядом Фурье функции \(f(x)\) по ортогональной системе функций \(\<\varphi_(x)\>\). Так как этот ряд может оказаться расходящимся, то будем писать
$$
f(x) \sim \sum_^ <\infty>a_\varphi_(x).\label
$$
В частности, для тригонометрической системы \eqref формула \eqref имеет следующий вид:
$$
f(x) \sim \frac> <2>+ \sum_^ <\infty>a_ \cos \frac + b_ \sin \frac.\label
$$

Запись \eqref означает, что \(\sum_^ <\infty>a_\varphi_(x)\) есть ряд Фурье функции \(f(x)\) по ортогональной системе \(\(x)\>\).

Источник

Теория графов. Основные понятия и виды графов

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Теория графов

В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.

Теория графов — обширный раздел дискретной математики, в котором системно изучают свойства графов.

Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.

Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.

Давайте на примере.

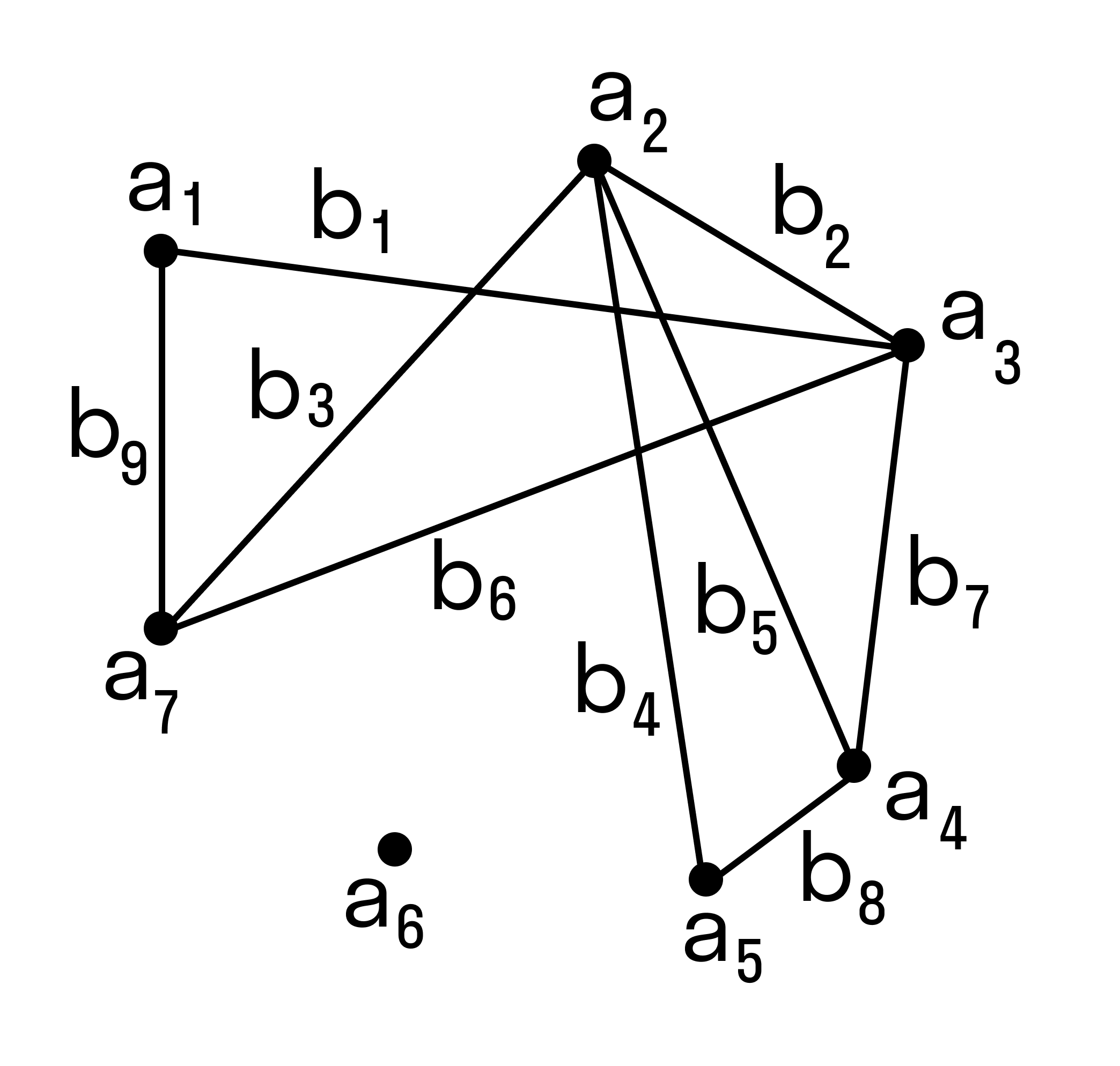
На множестве A зададим отношение знакомства между людьми из этого множества. Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.

Число знакомых у одних людей может отличаться от числа знакомых у других людей, некоторые могут вовсе не быть знакомы (такие элементы будут точками, не соединёнными ни с какой другой). Так получился граф:

В данном случае точки — это вершины графа, а связки — рёбра графа.

Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество разных задач, при решении которых можно временно забыть о содержании множеств и их элементов. Эта специфика не отражается на ходе решения задачи.

Например, вопрос в задаче стоит так: можно ли из точки A добраться до точки E, если двигаться только по соединяющим точки линиям. Когда задача решена, мы получаем решение, верное для любого содержания, которое можно смоделировать в виде графа.

Не удивительно, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с человеком вопросы отношений, географии или музыки, решения различных задач.

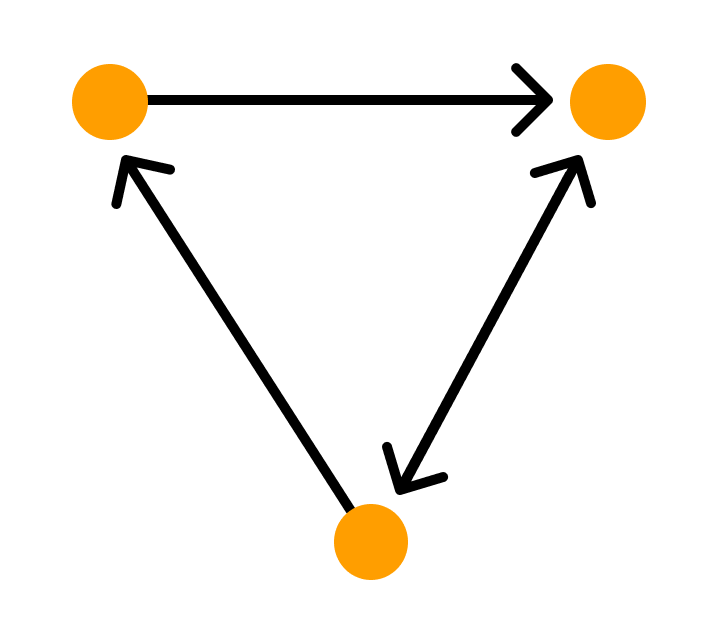
Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.

Пусть V — (непустое) множество вершин, элементы v ∈ V — вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a, b ∈ V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество ребер e графа. Вершины a и b — концевые точки ребра e.

Широкое применение теории графов в компьютерных науках и информационных технологиях можно объяснить понятием графа как структуры данных. В компьютерных науках и информационных технологиях граф можно описать, как нелинейную структуру данных.

Линейные структуры данных особенны тем, что связывают элементы отношениями по типу «простого соседства». Линейными структурами данных можно назвать массивы, таблицы, списки, очереди, стеки, строки. В нелинейных структурах данных элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порожденные и подобные.

Основные понятия теории графов

Граф — это геометрическая фигура, которая состоит из точек и линий, которые их соединяют. Точки называют вершинами графа, а линии — ребрами.

Лемма о рукопожатиях

В любом графе сумма степеней всех вершин равна удвоенному числу ребер.

Доказательство леммы о рукопожатиях

Если ребро соединяет две различные вершины графа, то при подсчете суммы степеней вершин мы учтем это ребро дважды.

Если же ребро является петлей — при подсчете суммы степеней вершин мы также учтем его дважды (по определению степени вершины).

Из леммы о рукопожатиях следует: в любом графе число вершин нечетной степени — четно.

Пример 1. В классе 30 человек. Может ли быть так, что у 9 из них есть 3 друга в этом классе, у 11 — 4 друга, а у 10 — 5 друзей? Учесть, что дружбы взаимные.

Если бы это было возможно, то можно было бы нарисовать граф с 30 вершинами, 9 из которых имели бы степень 3, 11 — со степенью 4, 10 — со степенью 5. Однако у такого графа 19 нечетных вершин, что противоречит следствию из леммы о рукопожатиях.

Пример 2. Каждый из 102 учеников одной школы знаком не менее чем с 68 другими. Доказать, что среди них найдутся четверо ребят с одинаковым числом знакомых.

Сначала предположим противоположное. Тогда для каждого числа от 68 до 101 есть не более трех человек с таким числом знакомых. С другой стороны, у нас есть ровно 34 натуральных числа, начиная с 68 и заканчивая 101, а 102 = 34 * 3.

Это значит, что для каждого числа от 68 до 101 есть ровно три человека, имеющих такое число знакомых. Но тогда количество людей, имеющих нечетное число знакомых, нечетно. Противоречие.

Путь и цепь в графе

Путем или цепью в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Циклом называют путь, в котором первая и последняя вершины совпадают.

Путь или цикл называют простым, если ребра в нем не повторяются.

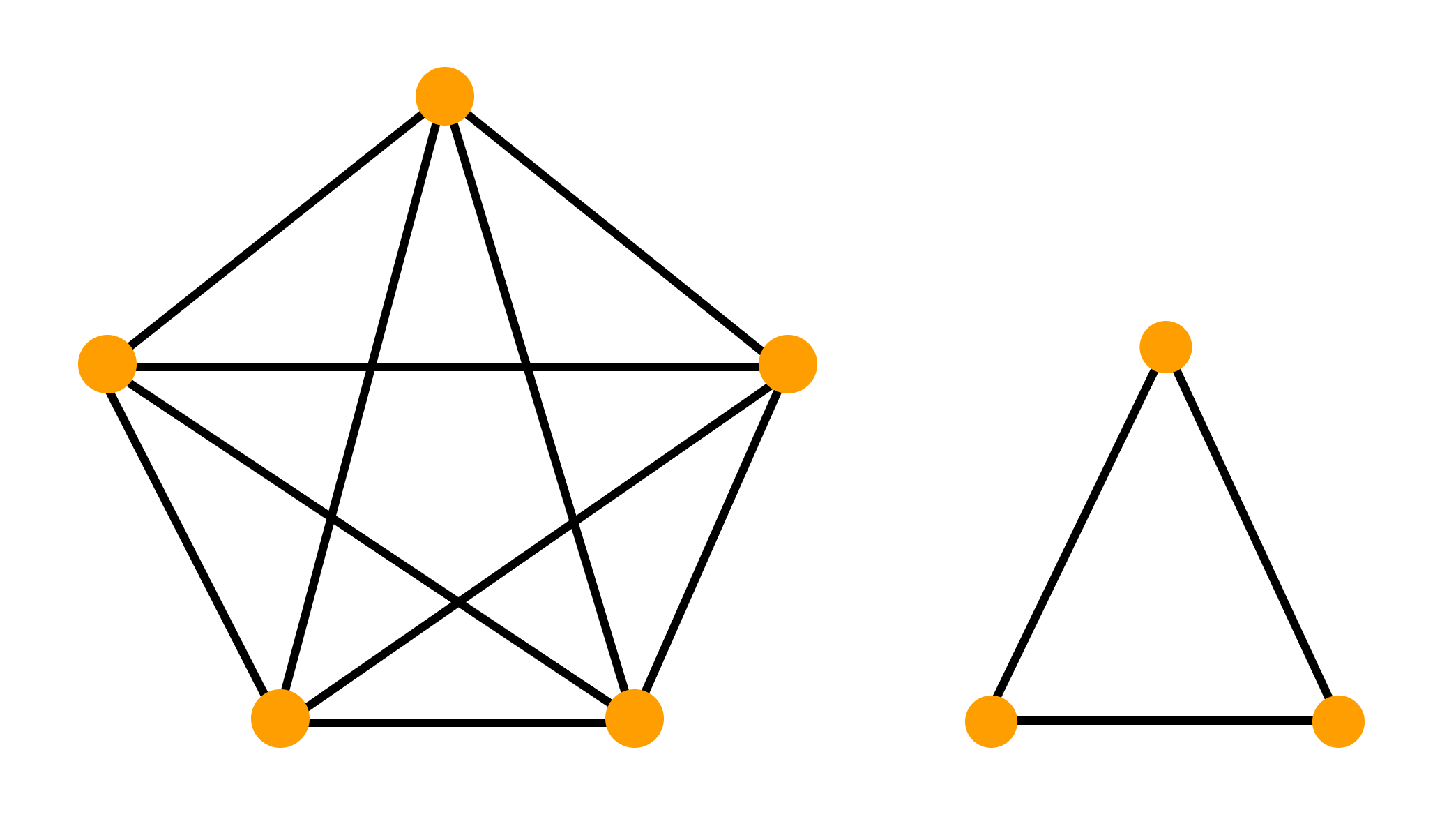
Если в графе любые две вершины соединены путем, то такой граф называется связным.

Можно рассмотреть такое подмножество вершин графа, что каждые две вершины этого подмножества соединены путем, а никакая другая вершина не соединена ни с какой вершиной этого подмножества.

Каждое такое подмножество, вместе со всеми ребрами исходного графа, соединяющими вершины этого подмножества, называется компонентой связности.

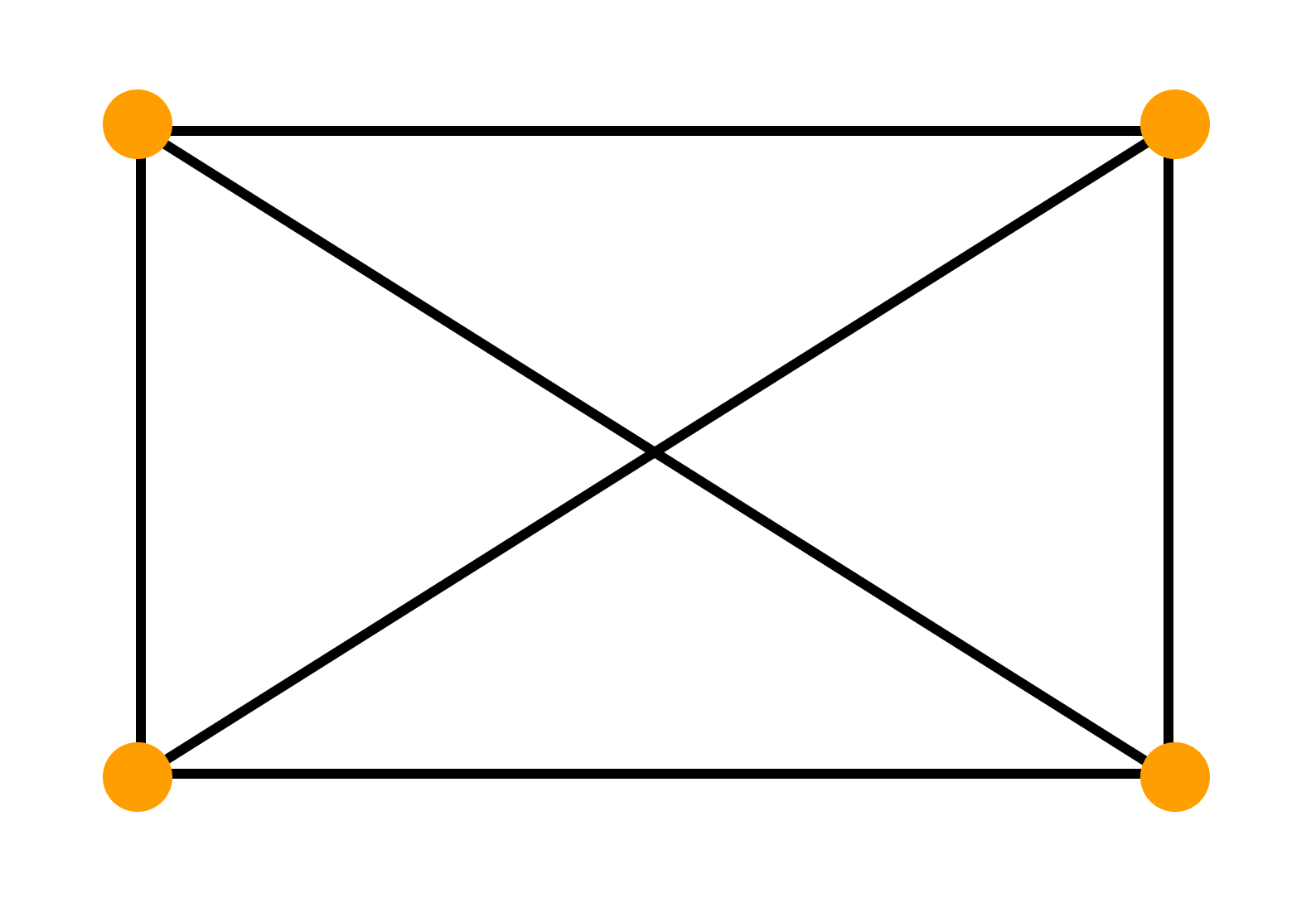
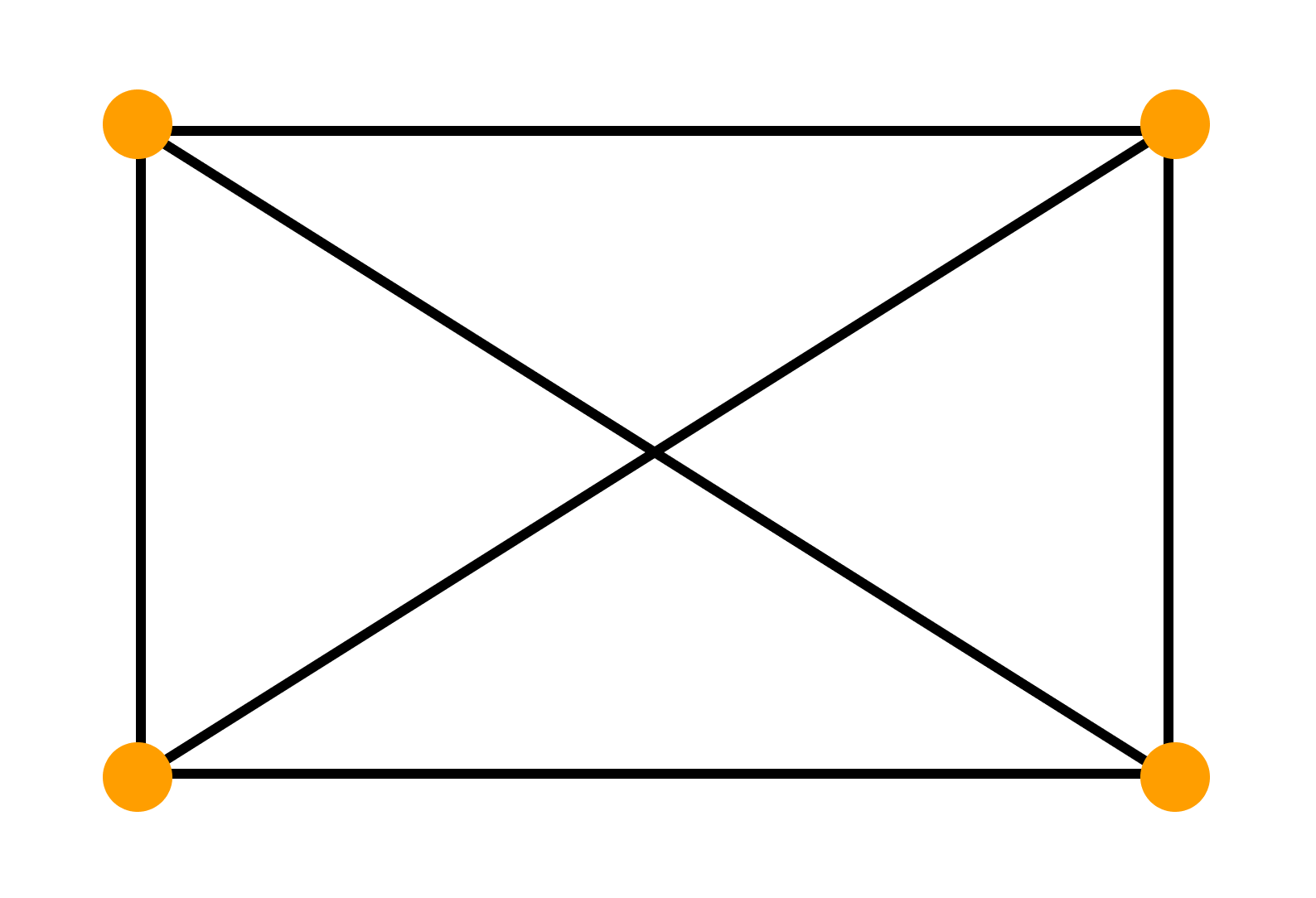
Один и тот же граф можно нарисовать разными способами. Вот, например, два изображения одного и того же графа, которые различаются кривизной:

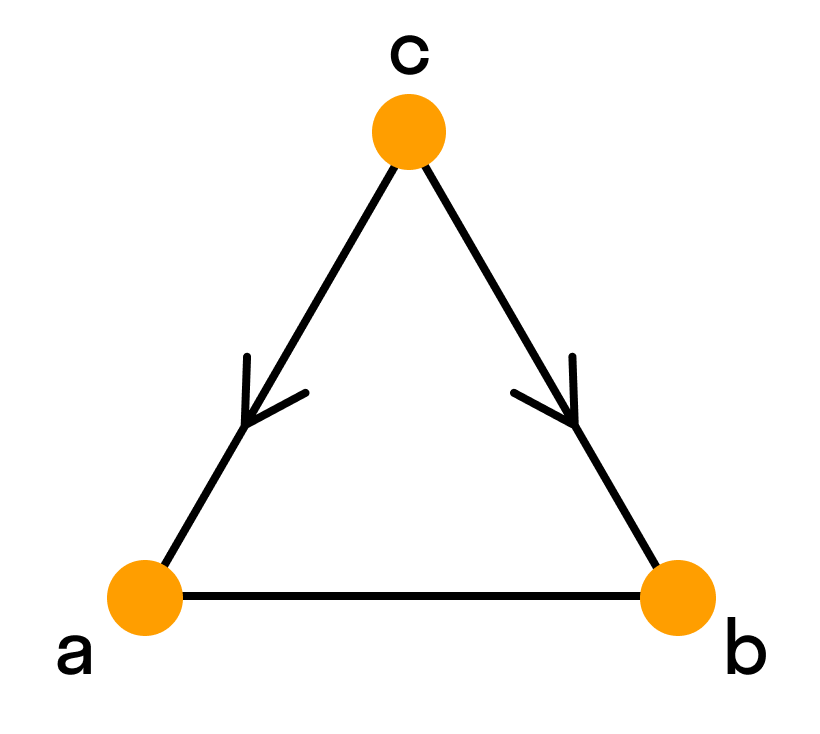
Два графа называются изоморфными, если у них поровну вершин. При этом вершины каждого графа можно занумеровать числами так, чтобы вершины первого графа были соединены ребром тогда и только тогда, когда соединены ребром соответствующие занумерованные теми же числами вершины второго графа.

Граф H, множество вершин V’ которого является подмножеством вершин V данного графа G и множество рёбер которого является подмножеством рёбер графа G соединяющими вершины из V’ называется подграфом графа G.

Визуализация графовых моделей

Визуализация — это процесс преобразования больших и сложных видов абстрактной информации в интуитивно-понятную визуальную форму. Другими словами, когда мы рисуем то, что нам непонятно — и сразу все встает на свои места.

Графы — и есть помощники в этом деле. Они помогают представить любую информацию, которую можно промоделировать в виде объектов и связей между ними.

Граф можно нарисовать на плоскости или в трехмерном пространстве. Его можно изобразить целиком, частично или иерархически.

Изобразительное соглашение — одно из основных правил, которому должно удовлетворять изображение графа, чтобы быть допустимым. Например, при изображении блок-схемы программы можно использовать соглашение о том, что все вершины должны изображаться прямоугольниками, а дуги — ломаными линиями с вертикальными и горизонтальными звеньями. При этом, конкретный вид соглашения может быть достаточно сложен и включать много деталей.

Виды изобразительных соглашений:

Виды графов

Виды графов можно определять по тому, как их построили или по свойствам вершин или ребер.

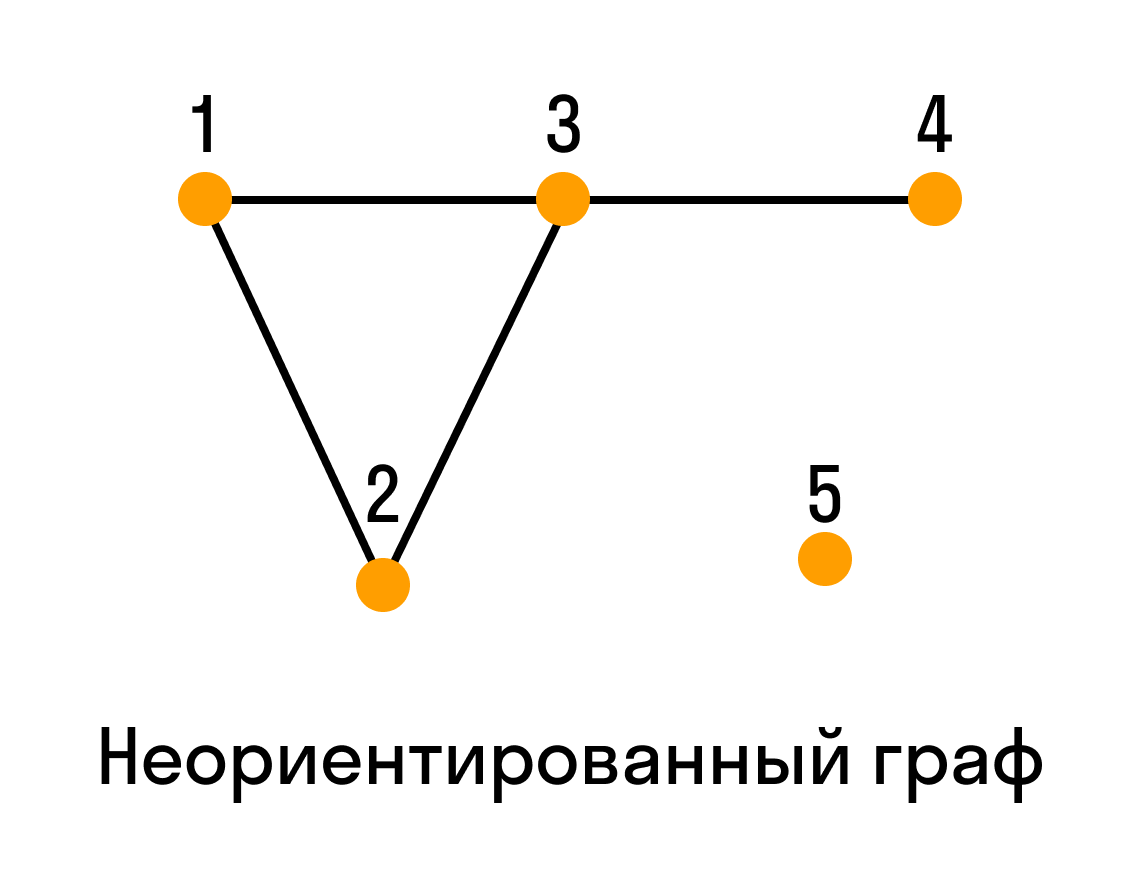
Ориентированные и неориентированные графы

Графы, в которых все ребра являются звеньями, то есть порядок двух концов ребра графа не существенен, называются неориентированными.

Графы, в которых все ребра являются дугами, то есть порядок двух концов ребра графа существенен, называются ориентированными графами или орграфами.

Неориентированный граф можно представить в виде ориентированного графа, если каждое его звено заменить на две дуги с противоположным направлением.

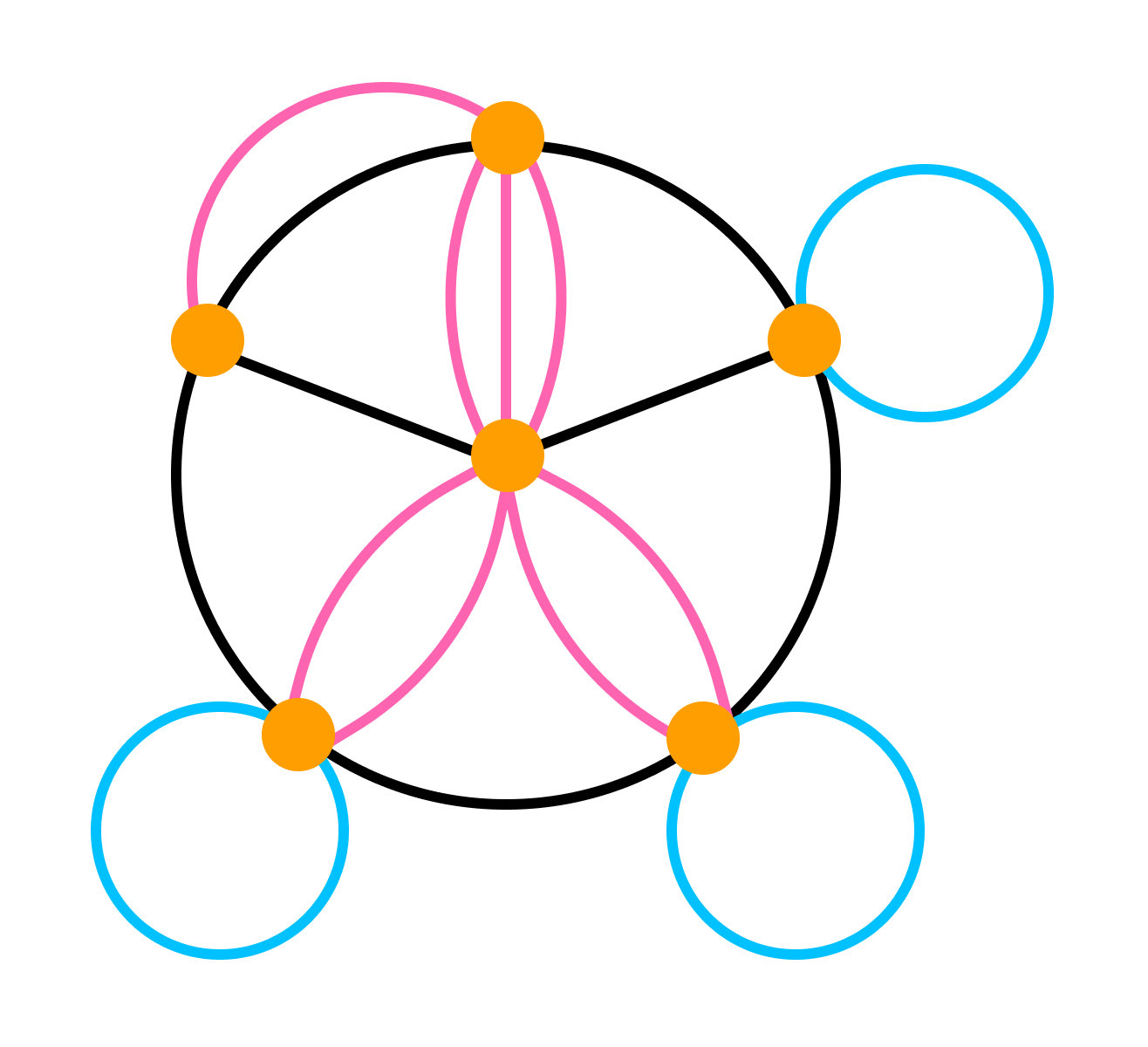
Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы

Если граф содержит петли — это обстоятельство важно озвучивать и добавлять к основной характеристике графа уточнение «с петлями». Если граф не содержит петель, то добавляют «без петель».

Смешанным называют граф, в котором есть ребра хотя бы двух из упомянутых трех разновидностей (звенья, дуги, петли).

Пустой граф — это тот, что состоит только из голых вершин.

Мультиграфом — такой граф, в котором пары вершин соединены более, чем одним ребром. То есть есть кратные рёбра, но нет петель.

Граф без дуг, то есть неориентированный, без петель и кратных ребер называется обыкновенным.

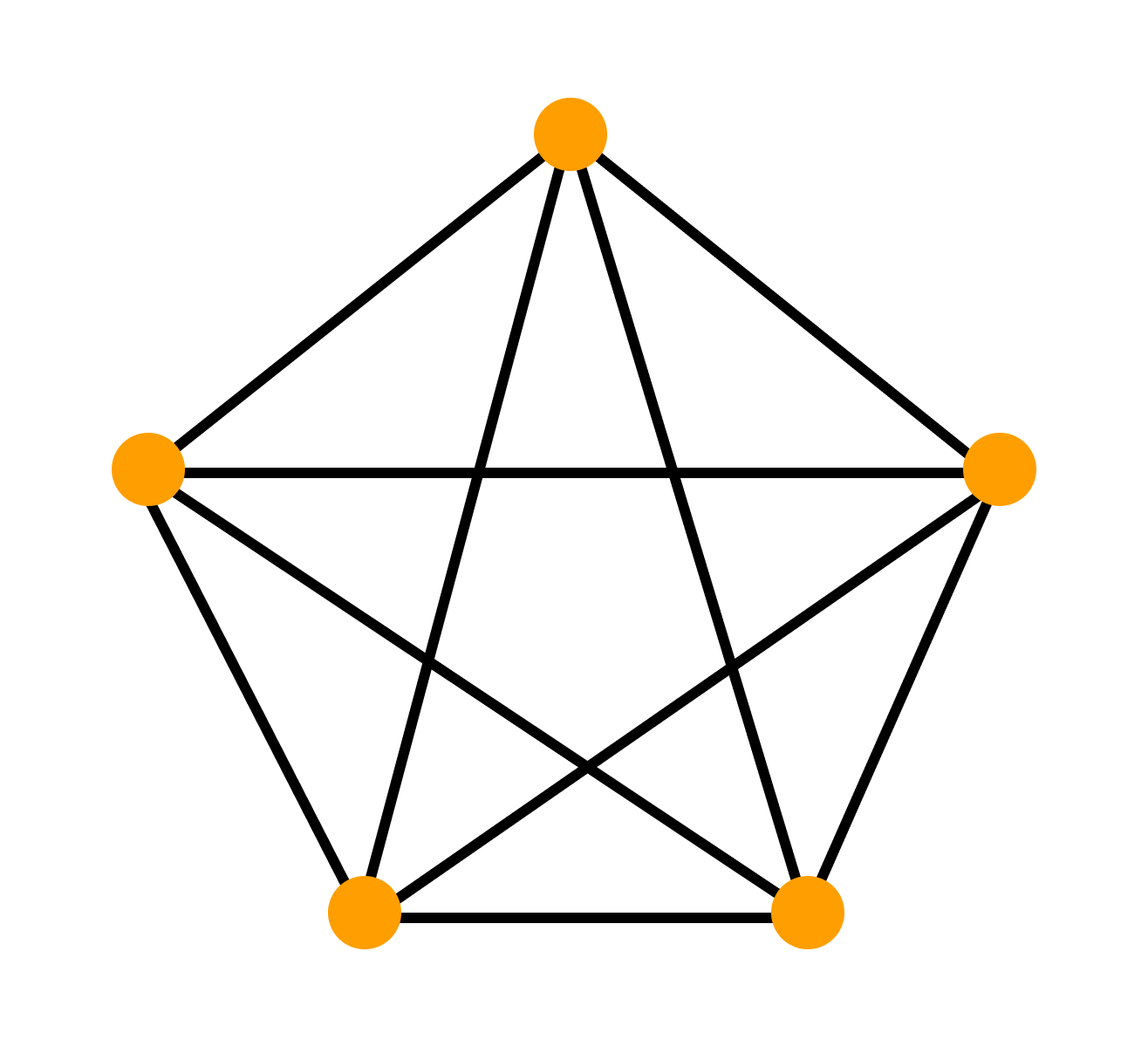
Граф называют полным, если он содержит все возможные для этого типа рёбра при неизменном множестве вершин. Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном.

Двудольный граф

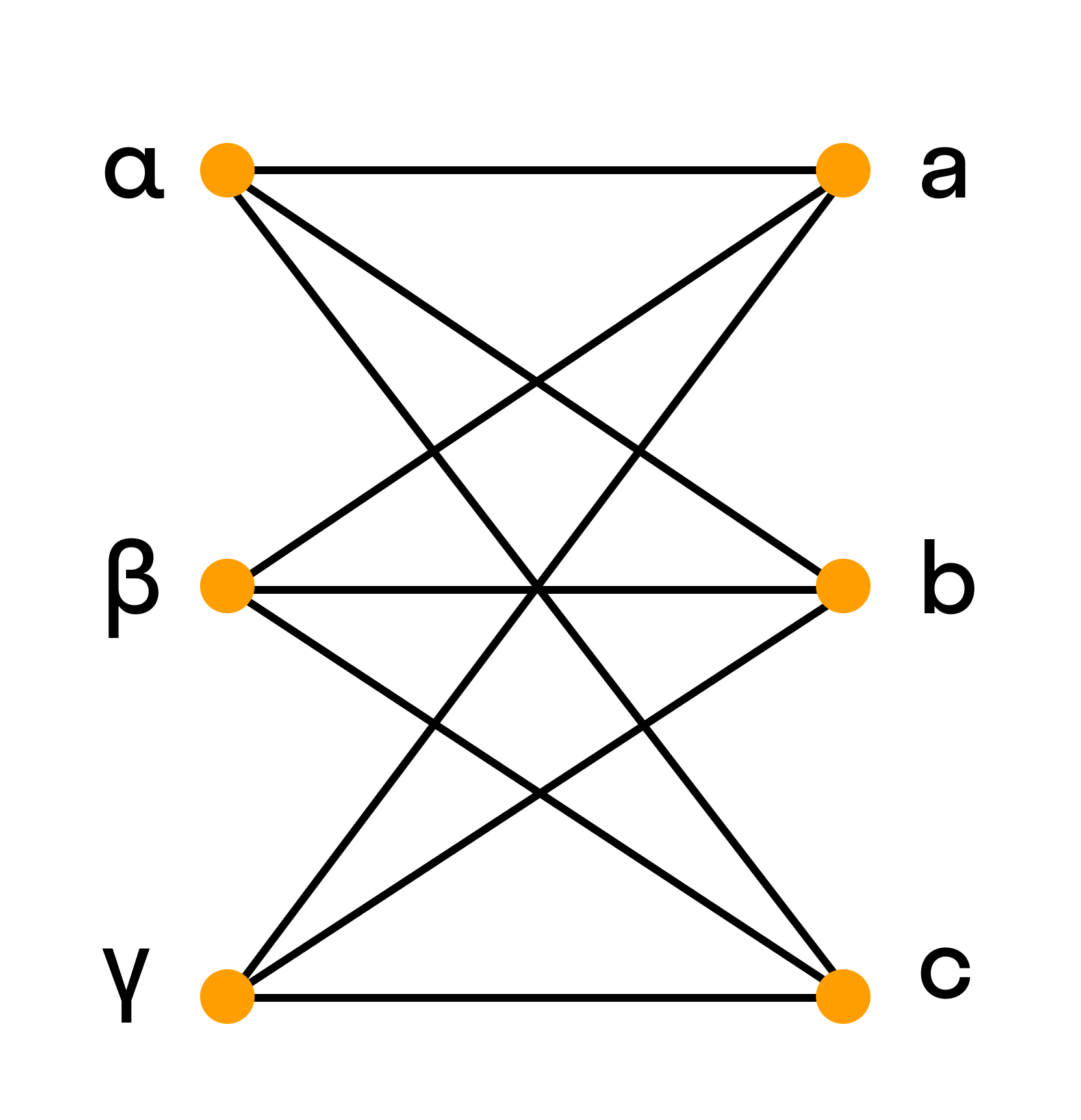
Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.

Например, полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, которые соединяют вершины одного множества с вершинами другого множества.

Эйлеров граф

Эйлеров граф отличен тем, что в нем можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.

Пример. Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом?

Регулярный граф

Регулярным графом называется связный граф, все вершины которого имеют одинаковую степень k.

Число вершин регулярного графа k-й степени не может быть меньше k + 1. У регулярного графа нечётной степени может быть лишь чётное число вершин.

Пример. Построить регулярный граф, в котором самый короткий цикл имеет длину 4.

Чтобы длина цикла соответствовала заданному условию, нужно чтобы число вершин графа было кратно четырем. Если число вершин равно четырём — получится регулярный граф, в котором самый короткий цикл имеет длину 3.

Увеличим число вершин до восьми (следующее кратное четырем число). Соединим вершины ребрами так, чтобы степени вершин были равны трём. Получаем следующий граф, удовлетворяющий условиям задачи:

Гамильтонов граф

Гамильтоновым графом называется граф, содержащий гамильтонов цикл.

Гамильтоновым циклом называется простой цикл, который проходит через все вершины рассматриваемого графа.

Говоря проще, гамильтонов граф — это такой граф, в котором можно обойти все вершины, и каждая вершина при обходе повторяется лишь один раз.

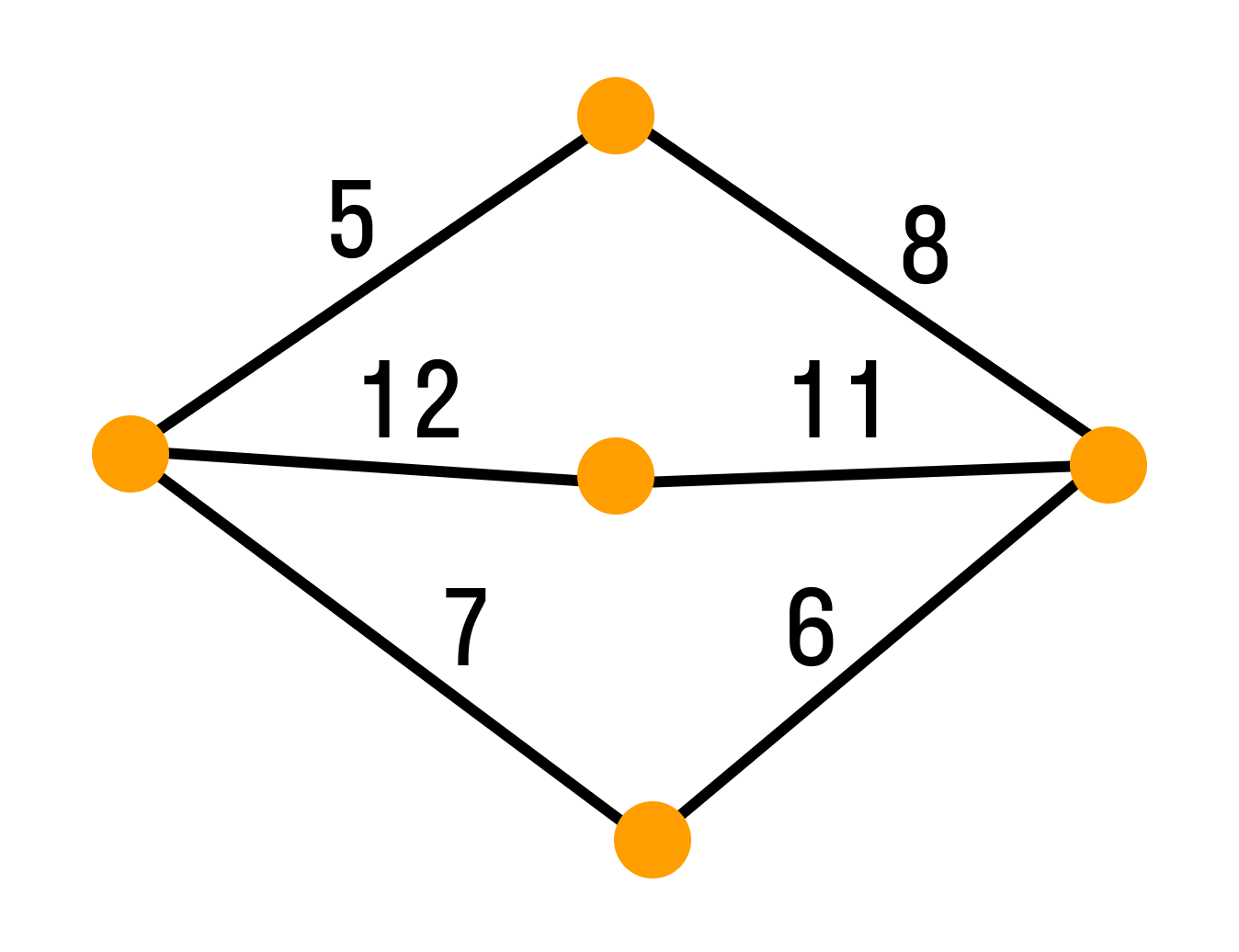
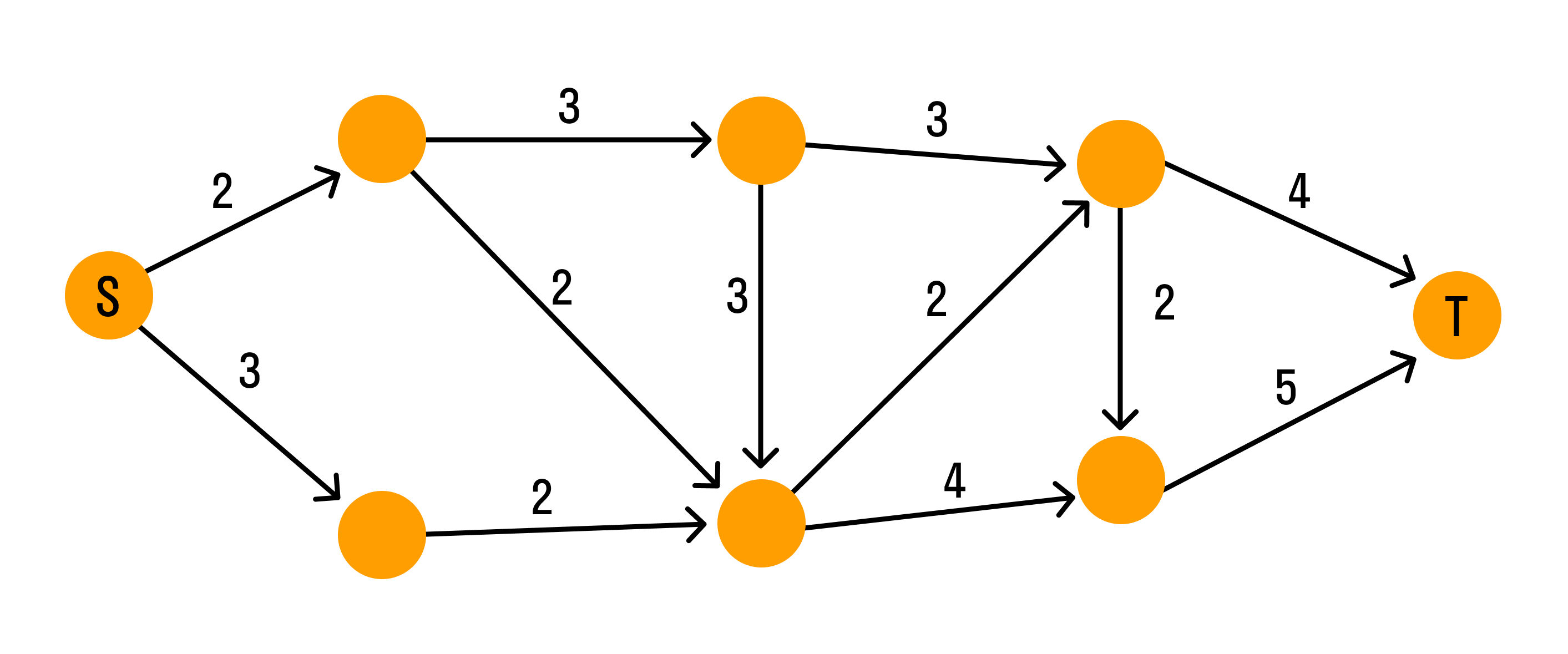
Взвешенный граф

Взвешенным графом называется граф, вершинам и/или ребрам которого присвоены «весы» — обычно некоторые числа. Пример взвешенного графа — транспортная сеть, в которой ребрам присвоены весы: они показывают стоимость перевозки груза по ребру и пропускные способности дуг.

Графы-деревья

Деревом называется связный граф без циклов. Любые две вершины дерева соединены лишь одним маршрутом.

Приведенное соотношение выражает критическое значение числа рёбер дерева, так как, если мы присоединим к дереву ещё одно ребро — будет создан цикл. А если уберем одно ребро, то граф-дерево разделится на две компоненты. Граф, состоящий из компонент дерева, называется лесом.

Определение дерева

Деревом называется связный граф, который не содержит циклов.

Таким образом, в дереве невозможно вернуться в исходную вершину, перемещаясь по ребрам и не проходя по одному ребру два или более раз.

Циклом называется замкнутый путь, который не проходит дважды через одну и ту же вершину.

Простым путем называется путь, в котором никакое ребро не встречается дважды.

Легко проверить, что дерево — это граф, в котором любые две вершины соединены ровно одним простым путем. Если выкинуть любое ребро из дерева, то граф станет несвязным. Поэтому:

Дерево — минимальный по числу рёбер связный граф.

Висячей вершиной называется вершина, из которой выходит ровно одно ребро.

Определения дерева:

Очень часто в дереве выделяется одна вершина, которая называется корнем дерева. Дерево с выделенным корнем называют корневым или подвешенным деревом. Пример: генеалогическое дерево.

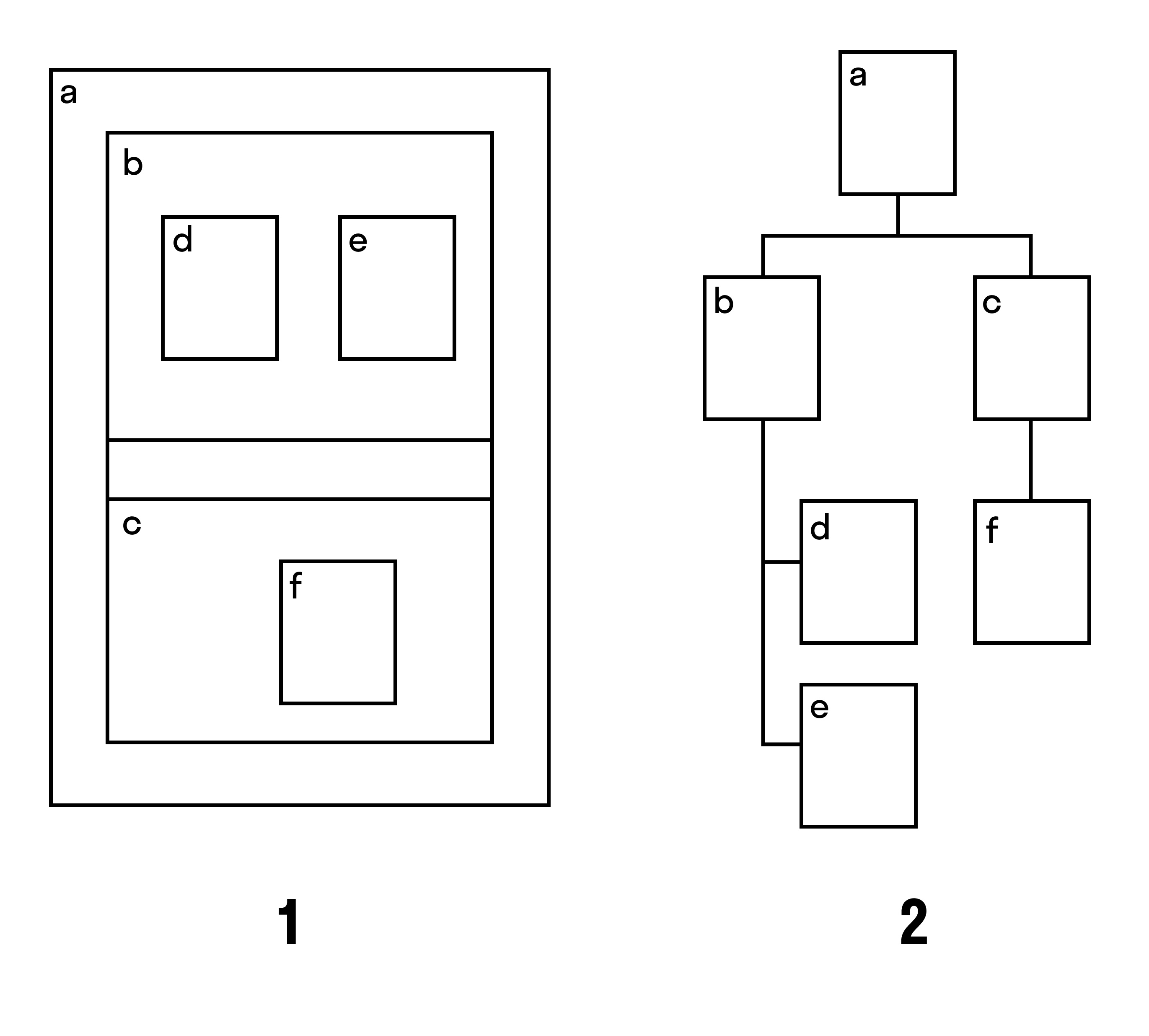
Когда изображают деревья, то часто применяют дополнительные соглашения, эстетические критерии и ограничения.

Например, при соглашении включения (рис. 1) вершины корневого дерева изображают прямоугольниками, а соглашение — опрокидывания (рис. 2) подобно классическому соглашению нисходящего плоского изображения корневого дерева. Вот так могут выглядеть разные изображения одного дерева:

Теоремы дерева и их доказательства

В дереве с более чем одной вершиной есть висячая вершина.

Доказательство первой теоремы:

Пойдем из какой-нибудь вершины по ребрам. Так как в дереве нет циклов, то мы не вернемся в вершину, в которой уже побывали. Если у каждой вершины степень больше 1, то найдется ребро, по которому можно уйти из неё после того, как мы пришли в нее.

Но поскольку количество вершин в дереве конечно, когда-нибудь мы остановимся в некоторой вершине. Противоречие. Значит, когда-нибудь мы дойдём в висячую вершину. Если же начать идти из неё, то мы найдём вторую висячую вершину.

В дереве число вершин на 1 больше числа ребер.

Доказательство второй теоремы:

Докажем по индукции по количеству вершин в дереве n. Если в дерево одна вершина, то факт верен. Предположим, что для всех n

У любого связного графа есть остовное дерево.

Доказательство третьей теоремы:

Чтобы найти остовное дерево графа G, можно найти цикл в графе G и выкинуть одно ребро цикла — потом повторить. И так пока в графе не останется циклов. Полученный граф будет связным, так как мы выкидывали рёбра, не нарушая связность, но в нём не будет циклов. Значит, он будет деревом.

Теория графов и современные прикладные задачи

На основе теории графов создали разные методы решения прикладных задач, в которых в виде графов можно моделировать сложные системы. В этих моделях узлы содержат отдельные компоненты, а ребра отражают связи между компонентами.

Графы и задача о потоках

Система водопроводных труб в виде графа выглядит так:

Каждая дуга графа отображает трубу. Числа над дугами (весы) — пропускная способность труб. Узлы — места соединения труб. Вода течёт по трубам только в одном направлении. Узел S — источник воды, узел T — сток.

Задача: максимизировать объём воды, протекающей от источника к стоку.

Для решения задачи о потоках можно использовать метод Форда-Фулкерсона. Идея метода в том, чтобы найти максимальный поток по шагам.

Сначала предполагают, что поток равен нулю. На каждом последующем шаге значение потока увеличивается, для чего ищут дополняющий путь, по которому поступает дополнительный поток. Эти шаги повторяют до тех пор, пока существуют дополнительные пути.

Задачу успешно применяют в различных распределенных системах: система электроснабжения, коммуникационная сеть, система железных дорог.

Графы и сетевое планирование

В задачах планирования сложных процессов, где много разных параллельных и последовательных работ, часто используют взвешенные графы. Их еще называют сетью ПЕРТ (PERT).

PERT (Program (Project) Evaluation and Review Technique) — техника оценки и анализа программ (проектов), которую используют при управлении проектами.

Сеть ПЕРТ — взвешенный ациклический ориентированный граф, в котором каждая дуга представляет работу (действие, операцию), а вес дуги — время, которое нужно на ее выполнение.

Если в сети есть дуги (a, b) и (b, c), то работа, представленная дугой (a, b), должна быть завершена до начала выполнения работы, представленной дугой (b, c). Каждая вершина (vi) представляет момент времени, к которому должны быть завершены все работы, задаваемые дугами, оканчивающимися в вершине (vi).

Путь максимальной длины между этими вершинами графа называется критическим путем. Чтобы выполнить всю работу быстрее, нужно найти задачи на критическом пути и придумать, как их выполнить быстрее. Например, нанять больше людей, перепридумать процесс или ввести новые технологии.

Источник

• ← Что такое гибриды в биологии
• Что такое мощность сигнала и как ее можно вычислить →