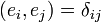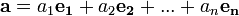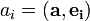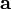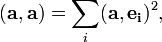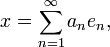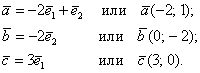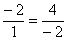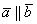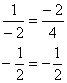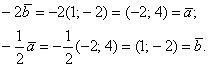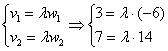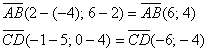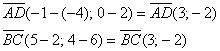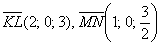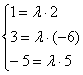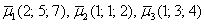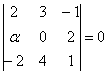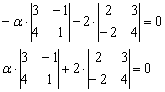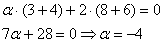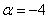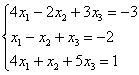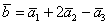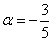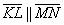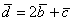Что такое ортонормированный базис в разложении векторов
Ортогональный и ортонормированный базисы евклидова пространства
Так как евклидово пространство является линейным, на него переносятся все понятия и свойства, относящиеся к линейному пространству, в частности, понятия базиса и размерности.
Теорема 8.5. В конечномерном евклидовом пространстве любую систему ортогональных (ортонормированных) векторов можно дополнить до ортогонального (ортонормированного) базиса.
В самом деле, по теореме 8.2 любую систему линейно независимых векторов, в частности, ортогональную (ортонормированную), можно дополнить до базиса. Применяя к этому базису процесс ортогонализации, получаем ортогональный базис. Нормируя векторы этого базиса (см. пункт 4 замечаний 8.11), получаем ортонормированный базис.
Выражение скалярного произведения через координаты сомножителей
Пусть [math]\mathbf
Выразим скалярное произведение, используя следствие 3 из аксиом скалярного произведения:
Преобразуем это выражение, используя операции с матрицами:
Преимущества ортонормированного базиса
Аналогично доказываются остальные формулы.
Изменение матрицы Грама при переходе от одного базиса к другому
По формуле (8.32) вычислим скалярное произведение векторов [math]\mathbf
Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому :
Свойства определителя Грама
Определитель матрицы (8.33) называется определителем Грама. Рассмотрим свойства этого определителя.
1. Критерий Грама линейной зависимости векторов: система векторов [math]\mathbf
Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.
Главный минор матрицы Грама системы [math]\mathbf
Действительно, в процессе ортогонализации по векторам [math]\mathbf
После первого шага определитель Грама не изменяется
Так как при этих преобразованиях определитель не изменяется, то
Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:
3. Определитель Грама любой системы [math]\mathbf
Следовательно, по свойству 2 имеем
1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.
2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.
3. Определитель квадратной матрицы [math]A[/math] (n-го порядка) удовлетворяет неравенству Адамара :
4. Если [math]A[/math] — невырожденная квадратная матрица, то любой главный минор матрицы [math]A^TA[/math] положителен. Это следует из пункта 2, учитывая представление произведения [math]A^TA=G(a_1,\ldots,a_n)[/math] как матрицы Грама системы линейно независимых векторов [math]a_1,\ldots,a_n[/math] — столбцов матрицы [math]A[/math] (см. пункт 3).
Изоморфизм евклидовых пространств
где [math](\cdot,\cdot)[/math] и [math](\cdot,\cdot)'[/math] — скалярные произведения в пространствах [math]\mathbb
Следовательно, евклидовы пространства [math]\mathbb
Таким образом, изучение конечномерных евклидовых пространств может быть сведено к исследованию вещественного арифметического пространства [math]\mathbb
Ортогональный и ортонормированный базисы
Система векторов называется ортогональной, если все векторы, образующие ее, попарно ортогональны. Система векторов называется ортонормировинной, если она ортогональная и длина каждого вектора равна единице.
Стандартные базисы на прямой, на плоскости, в пространстве
Базисы на прямой, на плоскости и в пространстве определяются не однозначно. Некоторые из них, наиболее удобные в приложениях, принимаются в качестве стандартных.
1. Стандартные базисы на плоскости и в пространстве ортонормированные, поэтому во всех приведенных разложениях вектор представляется в виде суммы своих ортогональных проекций на соответствующие прямые или оси, задаваемые базисными векторами (см. теорему 1.2), т.е.
2. Вектор в пространстве является замыкающей ломаной (см. правило сложения векторов), образованной его проекциями (рис.1.34,в):
3. Вектор в пространстве является суммой своих ортогональных составляющих
относительно плоскостей (рис.1.34,в):
4. Стандартные базисы на плоскости и в пространстве являются правыми.
5. Координаты вектора в стандартном базисе равны алгебраическим значениям длин его ортогональных проекций на координатные оси (рис.1.34,в):
6. В ортонормированием базисе длина вектора равна квадратному корню из суммы квадратов его координат:
Направляющие косинусы
В пространстве получаем аналогичные равенства:
При этом (см. пункт 3 теоремы 1.2).
Согласно (1.6), его координатами служат направляющие косинусы:
Ортонормированный базис
Ортогональный (ортонормированный) базис — ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты.
Конечномерный случай
Ортогональный базис — базис, составленный из попарно ортогональных векторов.
Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами.
Последнее удобно записывается при помощи дельта-символа Кронекера:
то есть скалярное произведение каждой пары базисных векторов равно нулю, когда они не совпадают (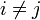
Очень многое записывается в ортонормированном базисе гораздо проще, чем в произвольном, поэтому очень часто стараются использовать именно такие базисы, если только это возможно или использование какого-то специального неортогонального базиса не дает особых специальных удобств. Или если не отказываются от него в пользу базиса общего вида из соображений общности.
Ортонормированный базис является самодуальным (дуальный ему базис совпадает с ним самим). Поэтому в нем можно не делать различия между верхними и нижними индексами, и пользоваться, скажем, только нижними (как обычно и принято, если конечно при этом используются только ортонормированные базисы).
Линейная независимость следует из ортогональности, то есть достигается для ортогональной системы векторов автоматически.
Разложение вектора по ортонормированному базису:
то есть каждый коэффициент разложения (координата) любого вектора в ортонормированном базисе равна просто скалярному произведению этого вектора на соответствующий базисный вектор.
Полнота ортонормированной системы векторов эквивалентна равенству Парсеваля: для любого вектора
то есть квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису.
Аналогичные соотношения имеют место и для бесконечномерного случая (см. ниже).
Бесконечномерный случай
Ортогональный базис — система попарно ортогональных элементов e1,e2. en. гильбертова пространства X такая, что любой элемент 
Необходимым и достаточным условием того, чтобы ортонормированная система <en> была базисом, является равенство Парсеваля
Гильбертово пространство, имеющее ортонормированный базис, является сепарабельным, и обратно, во всяком сепарабельном гильбертовом пространстве существует ортонормированный базис.
Если задана произвольная система чисел <an> такая, что 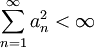
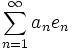

См. также
Полезное
Смотреть что такое «Ортонормированный базис» в других словарях:
ортонормированный базис — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN orthonormal basis … Справочник технического переводчика
БАЗИС — множества X минимальное порождающее его подмножество В. Порождение означает, что применением операций нек рого класса к элементам получается любой элемент Это понятие связано с понятием зависимости: элементы Xпосредством операций из ставятся в… … Математическая энциклопедия
Ортогональный базис — Ортогональный (ортонормированный) базис ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты. Содержание 1 Конечномерный случай 2 … Википедия
Метод главных компонент — (англ. Principal component analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих областях,… … Википедия
Истинное ортогональное разложение — Метод Главных Компонент (англ. Principal components analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих… … Википедия
Метод Главных Компонент — (англ. Principal components analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих областях, таких как… … Википедия
Преобразование Карунена-Лоэва — Метод Главных Компонент (англ. Principal components analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих… … Википедия
Преобразование Кархунена-Лоэва — Метод Главных Компонент (англ. Principal components analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих… … Википедия
Векторное пространство: размерность и базис, разложение вектора по базису
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Таким образом, мы пришли к формулировке важнейшей теоремы:
Докажем эту теорему:
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Вектор x → будет представлен следующим образом:
Запишем это выражение в координатной форме:
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
Решение
Используем метод Гаусса:
Пусть в базисе вектор x → имеет координаты x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
Указанные системы являются также базисами заданного пространства.
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
В виде матрицы систему можно отобразить так:
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
Линейная зависимость и линейная независимость векторов.
Базис векторов. Аффинная система координат
В аудитории находится тележка с шоколадками, и каждому посетителю сегодня достанется сладкая парочка – аналитическая геометрия с линейной алгеброй. В данной статье будут затронуты сразу два раздела высшей математики, и мы посмотрим, как они уживаются в одной обёртке. Сделай паузу, скушай «Твикс»! …блин, ну и чушь спорол. Хотя ладно, забивать не буду, в конце концов, на учёбу должен быть позитивный настрой.
Линейная зависимость векторов, линейная независимость векторов, базис векторов и др. термины имеют не только геометрическую интерпретацию, но, прежде всего, алгебраический смысл. Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства 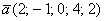
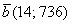
Нет, я не собираюсь грузить вас теорией, линейными векторными пространствами, задача состоит в том, чтобы понять определения и теоремы. Новые термины (линейная зависимость, независимость, линейная комбинация, базис и т.д.) приложимы ко всем векторам с алгебраической точки зрения, но примеры будут даны геометрические. Таким образом, всё просто, доступно и наглядно. Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания алгебры. Для освоения материала желательно ознакомиться с уроками Векторы для чайников и Как вычислить определитель?
Линейная зависимость и независимость векторов плоскости.
Базис плоскости и аффинная система координат
Рассмотрим плоскость вашего компьютерного стола (просто стола, тумбочки, пола, потолка, кому что нравится). Задача будет состоять в следующих действиях:
1) Выбрать базис плоскости. Грубо говоря, у столешницы есть длина и ширина, поэтому интуитивно понятно, что для построения базиса потребуется два вектора. Одного вектора явно мало, три вектора – лишка.
2) На основе выбранного базиса задать систему координат (координатную сетку), чтобы присвоить координаты всем находящимся на столе предметам.
Не удивляйтесь, сначала объяснения будут на пальцах. Причём, на ваших. Пожалуйста, поместите указательный палец левой руки на край столешницы так, чтобы он смотрел в монитор. Это будет вектор 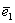
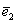
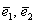
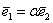
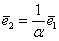
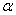
Картинку сего действа можно посмотреть на уроке Векторы для чайников, где я объяснял правило умножения вектора на число.
Будут ли ваши пальчики 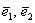
Такие векторы называют линейно зависимыми.
Справка: Слова «линейный», «линейно» обозначают тот факт, что в математических уравнениях, выражениях нет квадратов, кубов, других степеней, логарифмов, синусов и т.д. Есть только линейные (1-й степени) выражения и зависимости.
Два вектора плоскости линейно зависимы тогда и только тогда, когда они коллинеарны.
Скрестите пальцы на столе, чтобы между ними был любой угол, кроме 0 или 180 градусов. Два вектора плоскости 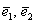
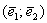
Любой вектор плоскости 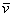
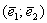
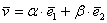
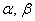
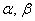
Также говорят, что вектор 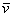
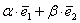
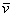
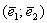
Например, можно сказать, что вектор 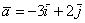
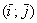
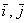
Сформулируем определение базиса формально: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов 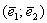
Существенным моментом определения является тот факт, что векторы взяты в определённом порядке. Базисы 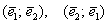
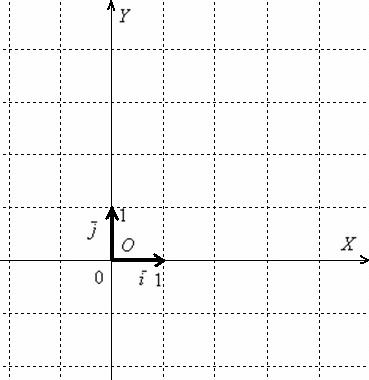
С базисом разобрались, но его недостаточно, чтобы задать координатную сетку и присвоить координаты каждому предмету вашего компьютерного стола. Почему недостаточно? Векторы являются свободными и блуждают по всей плоскости. Так как же присвоить координаты тем маленьким грязным точкам стола, которые остались после бурных выходных? Необходим отправной ориентир. И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:
Начну со «школьной» системы. Уже на вступительном уроке Векторы для чайников я выделял некоторые различия между прямоугольной системой координат и ортонормированным базисом 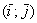
Когда говорят о прямоугольной системе координат, то чаще всего имеют в виду начало координат, координатные оси и масштаб по осям. Попробуйте набрать в поисковике «прямоугольная система координат», и вы увидите, что многие источники вам будут рассказывать про знакомые с 5-6-го класса координатные оси и о том, как откладывать точки на плоскости.
С другой стороны, создается впечатление, что прямоугольную систему координат вполне можно определить через ортонормированный базис 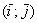
Точка 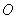
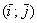
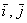
Думаю, всем понятно, что с помощью точки 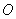
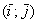
Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку 
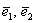
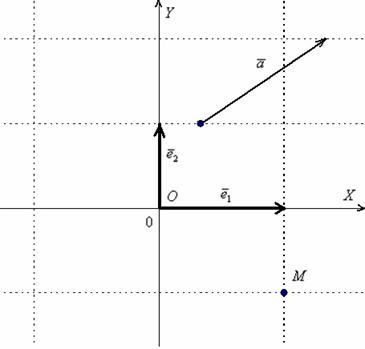
Такой базис называется ортогональным. Начало координат с векторами 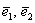
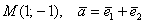
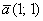
! Примечание: в ортогональном базисе, а также ниже в аффинных базисах плоскости и пространства единицы по осям считаются УСЛОВНЫМИ. Например, в одной единице по оси абсцисс содержится 4 см, в одной единице по оси ординат 2 см. Данной информации достаточно, чтобы при необходимости перевести «нестандартные» координаты в «наши обычные сантиметры».
И второй вопрос, на который уже на самом деле дан ответ – обязательно ли угол между базисными векторами должен равняться 90 градусам? Нет! Как гласит определение, базисные векторы должны быть лишь неколлинеарными. Соответственно угол может быть любым, кроме 0 и 180 градусов.
Точка 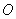
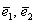
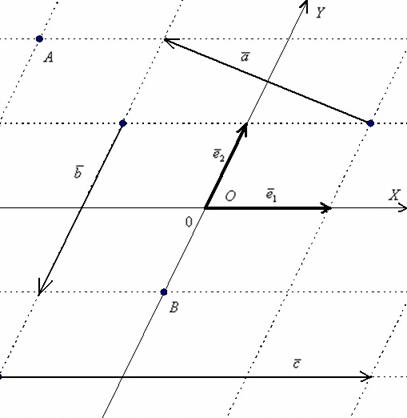
Иногда такую систему координат называют косоугольной системой. В качестве примеров на чертеже изображены точки 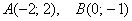
Как понимаете, аффинная система координат ещё менее удобна, в ней не работают формулы длин векторов и отрезков, которые мы рассматривали во второй части урока Векторы для чайников, многие вкусные формулы, связанные со скалярным произведением векторов. Зато справедливы правила сложения векторов и умножения вектора на число, формулы деления отрезка в данном отношении, а также ещё некоторые типы задач, которые мы скоро рассмотрим.
А вывод таков, что наиболее удобным частным случаем аффинной системы координат является декартова прямоугольная система. Поэтому её, родную, чаще всего и приходится лицезреть. …Впрочем, всё в этой жизни относительно – существует немало ситуаций, в которых уместна именно косоугольная (или какая-набудь другая, например, полярная) система координат. Да и гуманоидам такие системы могут прийтись по вкусу =)
Переходим к практической части. Все задачи данного урока справедливы как для прямоугольной системы координат, так и для общего аффинного случая. Сложного здесь ничего нет, весь материал доступен даже школьнику.
Как определить коллинеарность векторов плоскости?
Типовая вещь. Для того чтобы два вектора плоскости 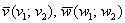
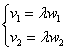
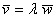
а) Проверить, коллинеарны ли векторы 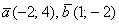
б) Образуют ли базис векторы 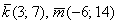
Решение:
а) Выясним, существует ли для векторов 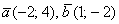
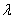
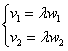
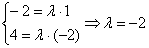
Обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне прокатывает на практике. Идея состоит в том, чтобы сразу составить пропорцию 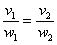
Составим пропорцию из отношений соответствующих координат векторов:
Сокращаем: 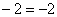
Отношение можно было составить и наоборот, это равноценный вариант:
Для самопроверки можно использовать то обстоятельство, что коллинеарные векторы линейно выражаются друг через друга. В данном случае имеют место равенства 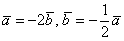
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Исследуем на коллинеарность векторы 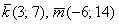
Из первого уравнения следует, что 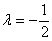
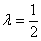
Вывод: векторы линейно независимы и образуют базис.
Упрощённая версия решения выглядит так:
Составим пропорцию из соответствующих координат векторов 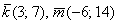
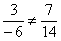
Обычно такой вариант не бракуют рецензенты, но возникает проблема в тех случаях, когда некоторые координаты равны нулю. Вот так: 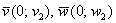
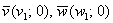
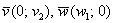
Ответ: а) 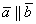
Небольшой творческий пример для самостоятельного решения:
При каком значении параметра 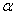
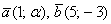
В образце решения параметр найден через пропорцию 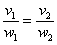
Существует изящный алгебраический способ проверки векторов на коллинеарность., систематизируем наши знания и пятым пунктом как раз добавим его:
Для двух векторов плоскости эквивалентны следующие утверждения:
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не коллинеарны;
4) векторы нельзя линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, отличен от нуля.
Соответственно, эквивалентны следующие противоположные утверждения:
1) векторы линейно зависимы;
2) векторы не образуют базиса;
3) векторы коллинеарны;
4) векторы можно линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, равен нулю.
Я очень и очень надеюсь, что на данный момент вам уже понятны все встретившиеся термины и утверждения.
Рассмотрим более подробно новый, пятый пункт: два вектора плоскости 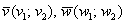
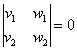
Решим Пример 1 вторым способом:
а) Вычислим определитель, составленный из координат векторов 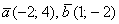
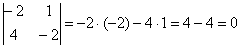
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Вычислим определитель, составленный из координат векторов 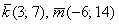
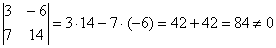
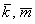
Ответ: а) 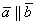
Выглядит значительно компактнее и симпатичнее, чем решение с пропорциями.
Проверка векторов на коллинеарность – простая и очень распространенная задача аналитической геометрии. Нередко в условии заодно требуется проверить векторы и на ортогональность (базис в таких случаях, как правило, ортонормированный). Данное задание подробно рассмотрено на уроке Скалярное произведение векторов.
С помощью рассмотренного материала можно устанавливать не только коллинеарность векторов, но и доказывать параллельность отрезков, прямых. Рассмотрим пару задач с конкретными геометрическими фигурами.
Даны вершины четырёхугольника 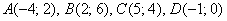
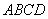
Доказательство: Чертежа в задаче строить не нужно, поскольку решение будет чисто аналитическим. Вспоминаем определение параллелограмма:
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Таким образом, нужно доказать:
1) параллельность противоположных сторон 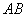
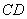
2) параллельность противоположных сторон 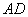
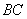
1) Найдём векторы:
Вычислим определитель, составленный из координат векторов 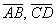
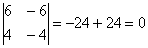
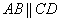
2) Найдём векторы:
Получился один и тот же вектор («по школьному» – равные векторы). Коллинеарность совсем очевидна, но решение таки лучше оформить с толком, с расстановкой. Вычислим определитель, составленный из координат векторов 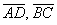
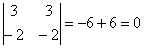
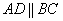
Вывод: Противоположные стороны четырёхугольника 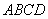
Больше фигур хороших и разных:
Даны вершины четырёхугольника 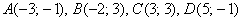
Для более строгой формулировки доказательства лучше, конечно, раздобыть определение трапеции, но достаточно и просто вспомнить, как она выглядит.
Это задание для самостоятельного решения. Полное решение в конце урока.
А теперь пора потихонечку перебираться из плоскости в пространство:
Как определить коллинеарность векторов пространства?
Правило очень похоже. Для того чтобы два вектора пространства 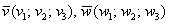
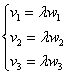
Выяснить, будут ли коллинеарны следующие векторы пространства:
а) 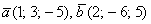
б) 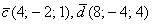
в)
Решение:
а) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
Система не имеет решения, значит, векторы 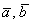
«Упрощёнка» оформляется проверкой пропорции 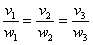
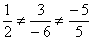
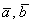
Ответ: векторы 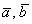
б-в) Это пункты для самостоятельного решения. Попробуйте его оформить двумя способами.
Существует метод проверки пространственных векторов на коллинеарность и через определитель третьего порядка, данный способ освещен в статье Векторное произведение векторов.
Аналогично плоскому случаю, рассмотренный инструментарий может применяться в целях исследования параллельности пространственных отрезков и прямых.
Добро пожаловать во второй раздел:
Линейная зависимость и независимость векторов трехмерного пространства.
Пространственный базис и аффинная система координат
Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Я постарался минимизировать конспект по теории, поскольку львиная доля информации уже разжёвана. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.
И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец. Это будут векторы 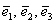
Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).
Определение: векторы называются компланарными, если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.
Три компланарных вектора всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы 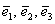
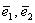
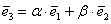
Справедливо и противоположное утверждение: три некомпланарных вектора всегда линейно независимы, то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.
Определение: Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов 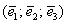
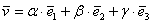
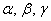
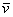
Напоминаю, также можно сказать, что вектор 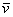
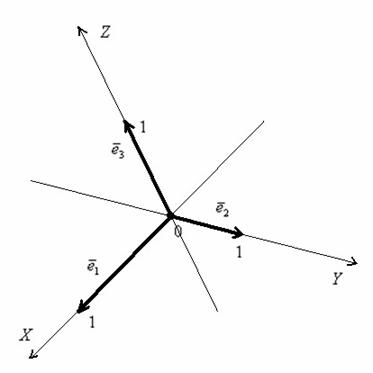
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов:
Точка 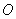
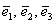
Конечно, координатная сетка «косая» и малоудобная, но, тем не менее, построенная система координат позволяет нам однозначно определить координаты любого вектора и координаты любой точки пространства. Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
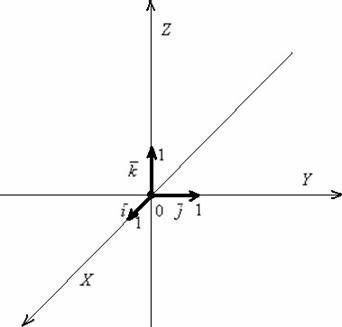
Наиболее привычным и удобным частным случаем аффинной системы координат, как все догадываются, является прямоугольная система координат пространства:
Точка 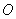
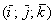
Перед тем, как перейти к практическим заданиям, вновь систематизируем информацию:
Для трёх векторов пространства эквивалентны следующие утверждения:
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.
Противоположные высказывания, думаю, понятны.
Три вектора пространства 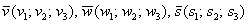
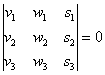
Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (значение определителя от этого не изменится – см. свойства определителей). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.
Тем читателям, которые немножко позабыли методы расчета определителей, а может и вообще слабо в них ориентируются, рекомендую один из моих самых старых уроков: Как вычислить определитель?
Проверить, образуют ли базис трёхмерного пространства следующие векторы:
а) 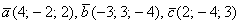
б)
Решение: Фактически всё решение сводится к вычислению определителя.
а) Вычислим определитель, составленный из координат векторов 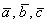
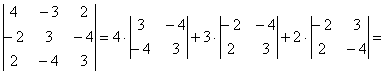
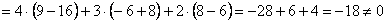
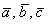
Ответ: данные векторы образуют базис
б) Это пункт для самостоятельного решения. Полное решение и ответ в конце урока.
Встречаются и творческие задачи:
При каком значении параметра 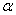
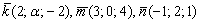
Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:
По существу, требуется решить уравнение с определителем. Налетаем на нули как коршуны на тушканчиков – определитель выгоднее всего раскрыть по второй строке и сразу же избавиться от минусов:
Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:
Ответ: при
Здесь легко выполнить проверку, для этого нужно подставить полученное значение 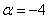
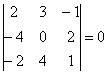
В заключение рассмотрим ещё одну типовую задачу, которая носит больше алгебраический характер и традиционно включается в курс линейной алгебры. Она настолько распространена, что заслуживает отдельного топика:
Доказать, что 3 вектора образуют базис трёхмерного пространства
и найти координаты 4-го вектора в данном базисе
Даны векторы 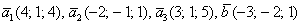
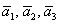
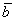
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора 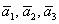
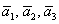
Вычислим определитель, составленный из координат векторов 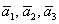
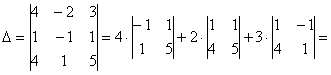
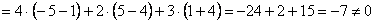
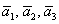
! Важно: координаты векторов 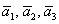
Теперь вспомним теоретическую часть: если векторы 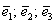
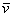
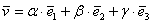
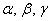
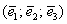
Поскольку наши векторы 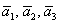
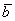
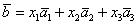
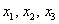
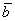
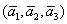
По условию и требуется найти координаты 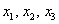
Для удобства объяснения поменяю части местами: 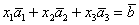
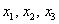
По какому принципу расставлены коэффициенты? Все коэффициенты левой части в точности перенесены из определителя 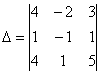
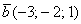
Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают по формулам Крамера, часто даже в условии задачи есть такое требование.
Главный определитель системы уже найден: 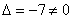
Дальнейшее – дело техники:
Таким образом:
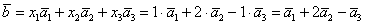
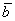
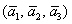
Ответ:
Более подготовленные читатели могут ознакомиться с уроком Переход к новому базису, и окончательно уяснить смысл прорешанной задачи. Кстати, с содержательной точки зрения использовать метод Крамера здесь – совсем не айс 😉
И, как я уже отмечал, задание носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, произвольные векторы курса линейной алгебры. Для случая двумерных векторов можно сформулировать и решить аналогичную задачу – решение будет технически намного проще, и поэтому я прошёл мимо него в предыдущем параграфе.
Такая же задача с трёхмерными векторами для самостоятельного решения:
Даны векторы 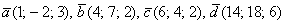
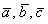
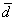
Полное решение и примерный образец чистового оформления в конце урока.
Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства, где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра.…Хотя, кто его знает, может быть и не чистая…, однако закругляемся – о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных, которая появилась раньше данного урока.
Любите векторы, и векторы полюбят вас!
Пример 2: Решение: составим пропорцию из соответствующих координат векторов: 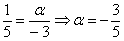
Ответ: при
Пример 4: Доказательство: трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
1) Проверим параллельность противоположных сторон 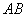
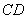
Найдём векторы: 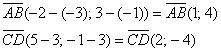
Вычислим определитель, составленный из координат векторов 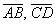
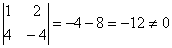
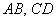
2) Проверим параллельность противоположных сторон 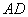
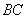
Найдём векторы: 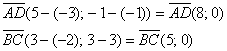
Вычислим определитель, составленный из координат векторов 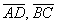
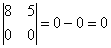
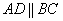
Вывод: Две стороны четырёхугольника 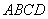
Пример 5: Решение:
б) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов: 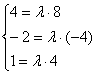
Система не имеет решения, значит, векторы 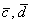
Более простое оформление:
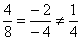
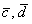
Ответ: векторы 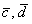
в) Исследуем на коллинеарность векторы 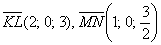
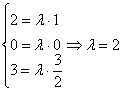
Соответствующие координаты векторов пропорциональны, значит 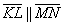
Вот здесь как раз не проходит «пижонский» метод оформления.
Ответ:
Пример 6: Решение: б) Вычислим определитель, составленный из координат векторов 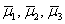
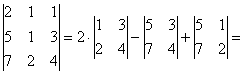
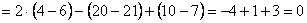
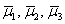
Ответ: данные векторы не образуют базиса
Пример 9: Решение: Вычислим определитель, составленный из координат векторов 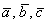

Таким образом, векторы 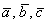
Представим вектор 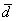
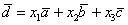
Покоординатно: 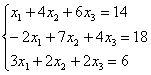
Систему решим по формулам Крамера: 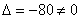
Ответ: Векторы 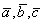
Автор: Емелин Александр
(Переход на главную страницу)