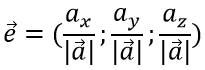Что такое орты осей
Единичный вектор
Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
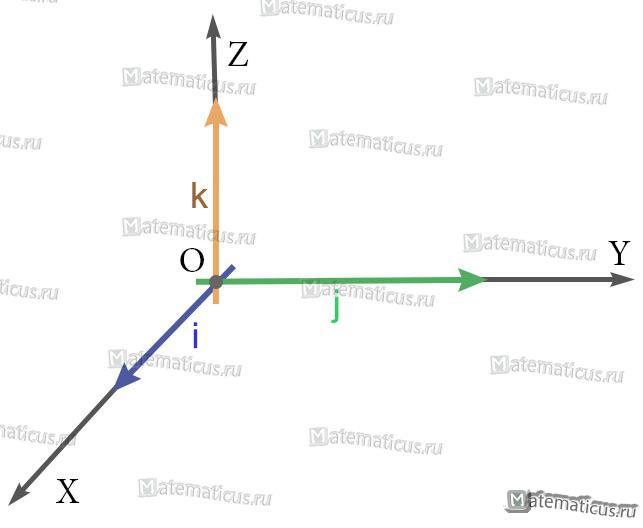
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0), j(0;1;0), k(0;0;1)
Единичные векторы являются некомпланарными.
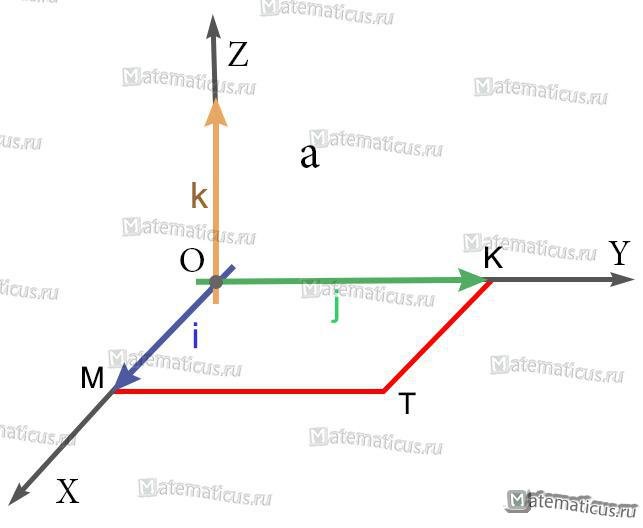
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Находим длину вектора a
затем вычисляем единичный вектор e
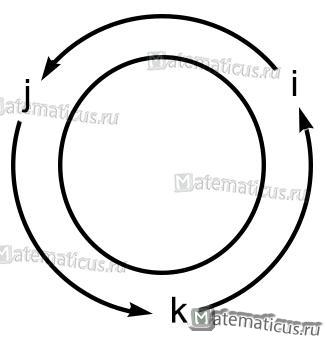
Векторное произведения единичных векторов
На основании схемы получаем таблицу векторного произведения единичных векторов
Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
iхj=k
Пример 2
Найти векторное произведение jхi.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.5 / 5. Количество оценок: 4
Декартова система координат
Прямоугольная, или декартова система координат — наиболее распространённая система координат на плоскости и в пространстве.
Содержание
Прямоугольная система координат на плоскости
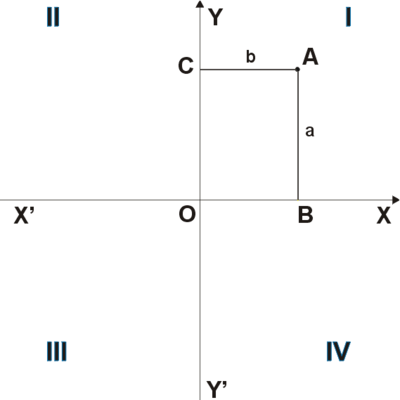
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).
Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве
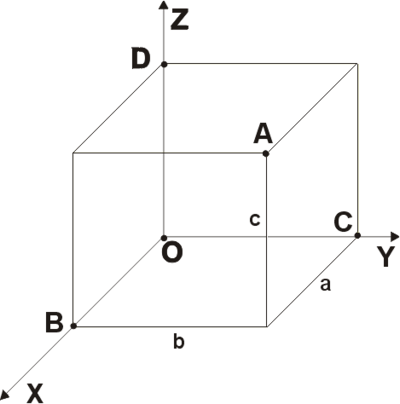
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).
Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
История
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
См. также
Ссылки
Полезное
Смотреть что такое «Декартова система координат» в других словарях:
ДЕКАРТОВА СИСТЕМА КООРДИНАТ — ДЕКАРТОВА СИСТЕМА КООРДИНАТ, прямолинейная система координат на плоскости или в пространстве (обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям). Названа по имени Р. Декарта (см. ДЕКАРТ Рене). Декарт впервые ввел… … Энциклопедический словарь
ДЕКАРТОВА СИСТЕМА КООРДИНАТ — прямоугольная система координат на плоскости или в пространстве, в которой масштабы по осям одинаковы и оси координат взаимно перпендикулярны. Д. с. к. обозначается буквами x:, у для точки на плоскости или x, у, z для точки в пространстве. (См.… … Большая политехническая энциклопедия
ДЕКАРТОВА СИСТЕМА КООРДИНАТ — ДЕКАРТОВА СИСТЕМА КООРДИНАТ, система, введенная Рене ДЕКАРТОМ, в которой положение точки определяется расстоянием от нее до взаимно пересекающихся линий (осей). В простейшем варианте системы оси (которые обозначаются как х и у) перпендикулярны.… … Научно-технический энциклопедический словарь
декартова система координат — Dekarto koordinačių sistema statusas T sritis fizika atitikmenys: angl. Cartesian system; Cartesian system of co ordinates vok. cartesisches Koordinatensystem, n; kartesisches Koordinatensystem, n rus. декартова система, f; декартова система… … Fizikos terminų žodynas
Декартова система координат — прямолинейная система координат (См. Координаты) на плоскости или в пространстве (обычно с одинаковыми масштабами по осям). Сам Р. Декарт в «Геометрии» (1637) употреблял только систему координат на плоскости (вообще, косоугольную). Часто… … Большая советская энциклопедия
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. В… … Википедия
декартова система — Dekarto koordinačių sistema statusas T sritis fizika atitikmenys: angl. Cartesian system; Cartesian system of co ordinates vok. cartesisches Koordinatensystem, n; kartesisches Koordinatensystem, n rus. декартова система, f; декартова система… … Fizikos terminų žodynas
СИСТЕМА КООРДИНАТ — совокупность условий, определяющих положение точки на прямой, на плоскости, в пространстве. Существуют различные С. к.: декартова, косоугольная, цилиндрическая, сферическая, криволинейная и др. Линейные и угловые величины, определяющие положение… … Большая политехническая энциклопедия
ДЕКАРТОВА ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ — ортонормированная прямолинейная система координат в евклидовом пространстве. Д. п. с. к. на плоскости задается двумя взаимно перпендикулярными прямыми осями координат, на каждой из к рых выбрано положительное направление и задан отрезок единичной … Математическая энциклопедия
Прямоугольная система координат — Прямоугольная система координат прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для… … Википедия
Декартовы координаты
Прямоугольная, или декартова система координат — наиболее распространённая система координат на плоскости и в пространстве.
Содержание
Прямоугольная система координат на плоскости
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).
Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).
Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
История
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
См. также
Ссылки
Полезное
Смотреть что такое «Декартовы координаты» в других словарях:
ДЕКАРТОВЫ КООРДИНАТЫ — (декартова система координат) система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные декартовы координаты. Названы по имени Р. Декарта … Большой Энциклопедический словарь
декартовы координаты — Система координат, состоящая из двух перпендикулярных осей. Положение точки в такой системе формируется с помощью двух чисел, определяющих расстояние от центра координат по каждой из осей. [http://www.morepc.ru/dict/] Тематики информационные… … Справочник технического переводчика
декартовы координаты — (декартова система координат), система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные декартовы координаты. Названы по имени Р. Декарта … Энциклопедический словарь
декартовы координаты — Dekarto koordinatės statusas T sritis Standartizacija ir metrologija apibrėžtis Tiesinė plokštumos arba erdvės koordinačių sistema. Joje ašių masteliai paprastai būna lygūs. atitikmenys: angl. Cartesian coordinates vok. kartesische Koordinaten, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
декартовы координаты — Dekarto koordinatės statusas T sritis fizika atitikmenys: angl. Cartesian coordinates; grid coordinates vok. kartesische Koordinaten, f rus. декартовы координаты, f pranc. coordonnées cartésiennes, f … Fizikos terminų žodynas
ДЕКАРТОВЫ КООРДИНАТЫ — способ определения положения точек на плоскости их расстояниями до двух фиксированных перпендикулярных прямых осей. Это понятие усматривается уже у Архимеда и Аппология Пергского более двух тысяч лет назад и даже у древних египтян. Впервые эта… … Математическая энциклопедия
ДЕКАРТОВЫ КООРДИНАТЫ — декартова система координат [по имени франц. философа и математика Р. Декарта (R. Descartes; 1596 1650)], система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные Д … Большой энциклопедический политехнический словарь
ДЕКАРТОВЫ КООРДИНАТЫ — (декартова система координат), система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные Д. к. Названы по имени Р. Декарта … Естествознание. Энциклопедический словарь
ДЕКАРТОВЫ КООРДИНАТЫ — Система расположения любой точки нашли кости относительно двух осей, перекрещивающихся под прямым углом. Разработанная Рене Декартом, эта система стала основой для стандартных методов графического представления данных. Горизонтальная линия… … Толковый словарь по психологии
Координаты — Координаты. На плоскости (слева) и в пространстве (справа). КООРДИНАТЫ (от латинского co совместно и ordinatus упорядоченный), числа, которые определяют положение точки на прямой, плоскости, поверхности, в пространстве. Координаты суть расстояния … Иллюстрированный энциклопедический словарь
Что такое орты осей
Получите бесплатный курс по основам математики. Эти знания необходимы для решения задач по физике.
Векторная алгебра с нуля!
Получите бесплатный курс по Векторной алгебре. Он необходим для решения задач по физике.
Книги по изучению физики и для подготовки к ЕГЭ
Единичные векторы. Орты. Декартова система координат
Очевидно, а = а·ае (а — модуль вектора а). Это следует из правила, по которому выполняется операция умножения скаляра на вектор.
Единичные векторы часто связывают с координатными осями системы координат (в частности, с осями декартовой системы координат). Направления этих векторов совпадают с направлениями соответствующих осей, а их начала часто совмещают с началом системы координат.
Дело в том, что, например, в механике при изучении движения тел прямоугольная система координат используется очень часто. Так вот, если сама система координат неподвижна, а изменение координат движущегося объекта отслеживается в этой неподвижной системе, то обычно оси обозначают X, Y, Z, а их орты соответственно i, j, k.
Но нередко, когда объект движется по какой-то криволинейной траектории (например, по окружности) бывает удобнее рассматривать механические процессы в системе координат, движущейся с этим объектом. Именно для такой движущейся системы координат и используются другие названия осей и их ортов. Просто так принято. В этом случае ось X направляют по касательной к траектории в той ее точке, в которой в данный момент этот объект находится. И тогда эту ось называют уже не осью X, а касательной осью, а ее орт обозначают уже не i, а τ. Ось Y направляют по радиусу кривизны траектории (в случае движения по окружности – к центру окружности). А поскольку радиус перпендикулярен касательной, то ось называют осью нормали (перпендикуляр и нормаль – это одно и то же). Орт этой оси обозначают уже не j, а n. Третья ось (бывшая Z) перпендикулярна двум предыдущим. Это – бинормаль с ортом b (рис. 12, справа). Кстати, в этом случае такую прямоугольную систему координат часто называют «естественной» или натуральной.
Книги по изучению физики и для подготовки к ЕГЭ
Эти книги должен иметь каждый старшеклассник, абитуриент и студент!
Пожалуйста, не забудьте поделиться о прочитанном со своими друзьями в соц. сетях (см. кнопки ниже).
Прямоугольная система координат. Ось абсцисс и ординат
Прямоугольная декартова система координат
Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.