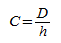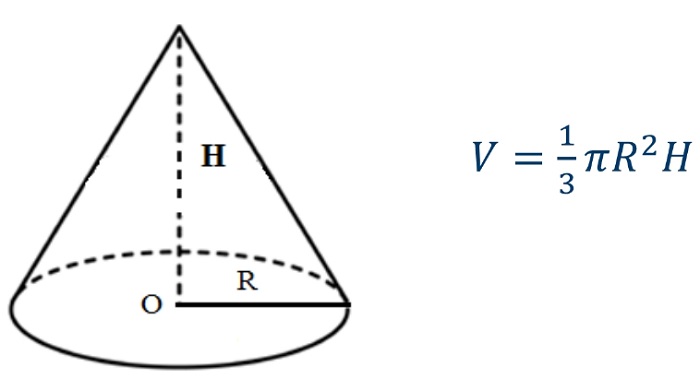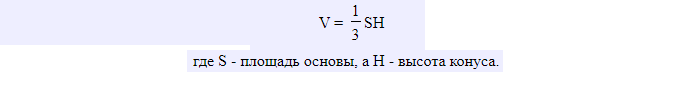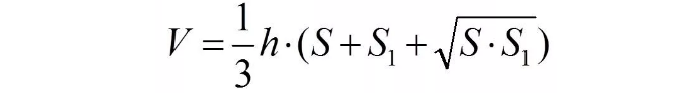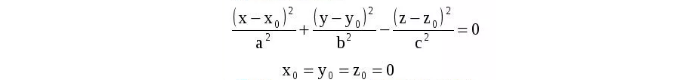Что такое ось конуса

Инструменты пользователя

Инструменты сайта

Боковая панель

Стереометрия:

Контакты

Конус

Конусом ( прямым круговым конусом ) называется тело, состоящее из круга ( основания конуса ), точки, не лежащей в плоскости этого круга ( вершины конуса ), и всех отрезков, соединяющих вершину конуса с точками основания.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.

Конус — тело, которое ограничено конической поверхностью и плоскостью, на которой лежат концы образующих конической поверхности.

Коническая поверхность — поверхность, которая образуется движением отрезка, один из концов которого неподвижен, а другой перемещается на плоскости вдоль некоторой кривой. Отрезки называют образующими конической поверхности, а кривую – направляющей. Неподвижная точка – вершина конической поверхности.

Боковая поверхность конуса — часть конической поверхности, ограниченная плоскостью.

Основание конуса — часть плоскости, отсекаемая боковой поверхностью конуса.

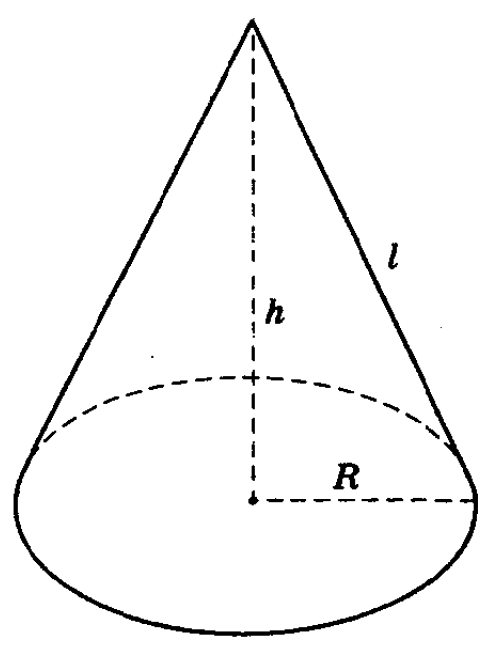
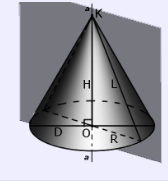
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания (См.Рис.1). В противном случае, конус называется наклонным. В школьном курсе изучается прямой круговой конус.

Круговой конус — конус, у которого в основании круг.

Прямой круговой конус ( просто конус ) — круговой конус, у которого прямая, соединяющая вершину конуса с центром круга, лежащего в основании, перпендикулярна плоскости основания.

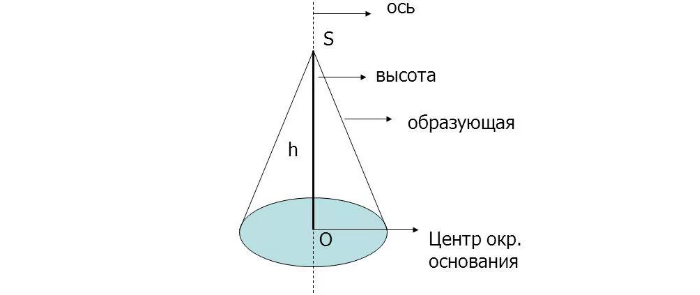
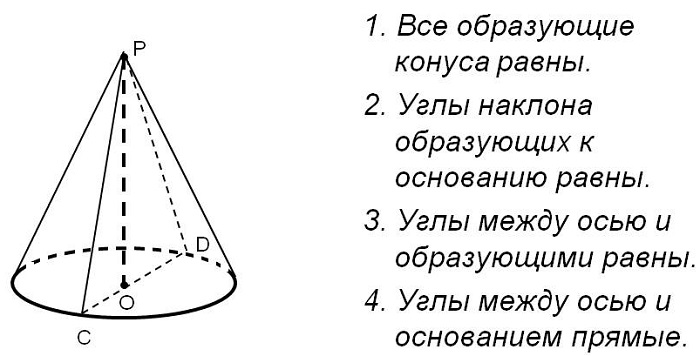
Ось конуса — прямая, проходящая через вершину конуса и центр основания конуса.

Высота конуса — отрезок оси конуса, соединяющий вершину конуса с центром основания.

Конус можно рассматривать как тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей его катет.

Образующие конуса совпадают с образующими конической поверхности.

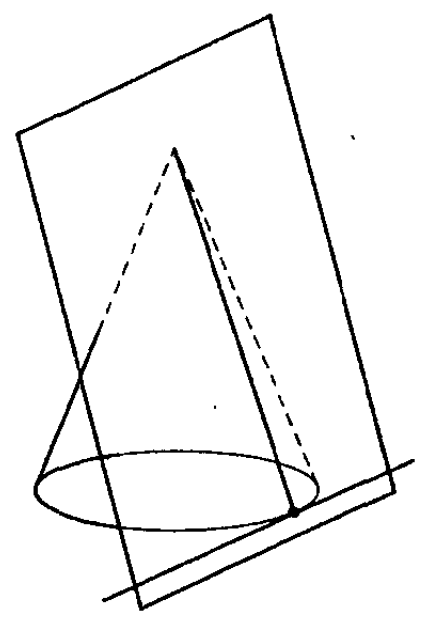
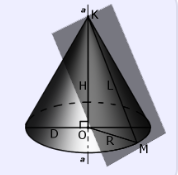
Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением. Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса. См.Рис.2.

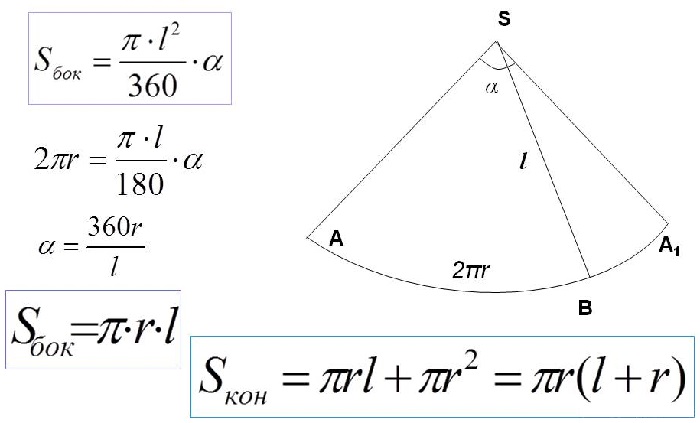
Развёртка боковой поверхности конуса — круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.

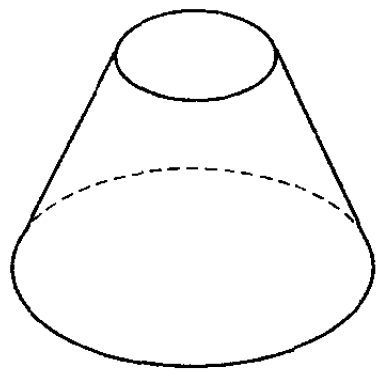
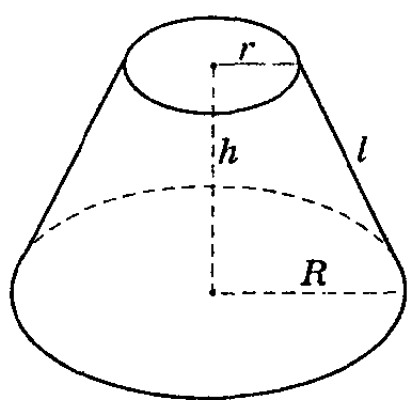
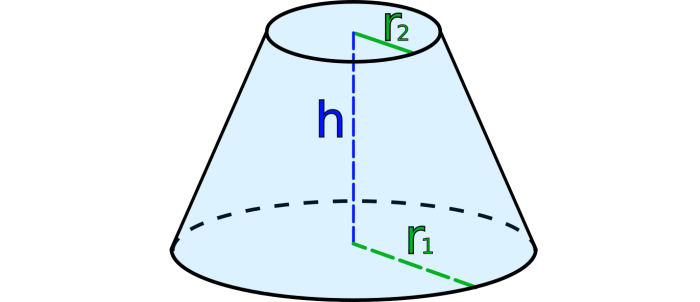
Усеченный конус – это часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания. См.Рис.3.

Видео-решение.

Инструменты страницы

Записаться на занятия

Источник

Из огромного перечня математических заданий часто встречаются задачи, связанные с темой «Конус». На уроках геометрии школьники должны усвоить основные понятия и названия всех элементов этой фигуры и понять, как и по каким формулам производится расчет нужных параметров.

О данной геометрической фигуре пойдёт речь в сегодняшней статье.

Определение и элементы конуса

Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.

При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.

Обратите внимание! Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.

Хотелось бы рассмотреть ещё несколько понятий по этой теме:

1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:

Важно! Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.

2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:

3. Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.

Свойства кругового конуса

Выделяют несколько особенностей, которыми обладает фигура данного типа:

Образующие кругового конуса равны друг другу.

Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.

Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.

Интересный факт! Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.

Общая формула объёма фигуры

Чтобы найти объём кругового конуса, необходимо умножить число Пи на его высоту, на радиус в квадрате и всё это произведение поделить на три:

Дополнительная информация! Чтобы узнать объём фигуры, нужно умножить площадь её основы на высоту и поделить на три:

Объём усечённого конуса

Это часть прямого конуса, которая находится в пространстве между основой и плоскостью, параллельной этому основанию. В общем виде выглядит следующим образом:

Объём данного тела можно вычислить по формуле:

Важно! S и S ₁ это площади соответствующих основ, которые равняются ПR 2 и ПR ₁ 2 При нахождении этих значений поможет онлайн калькулятор.

Площадь поверхности фигуры

Для вычисления данного параметра потребуется знать площадь боковой поверхности. Она равняется произведению числа π, радиуса и длины образующей.

Чтобы рассчитать площадь всей поверхности, нужно сложить площади его основы и боковой поверхности.

Площадь усечённого конуса

Для нахождения данного параметра нужно воспользоваться формулами:

площади боковой поверхности усечённого конуса S_бок;

полной площади усечённой фигуры S_пол, которая равна сумме площадей двух оснований и площади боковой поверхности:

Уравнение конуса

Часто требуется при решении математических задач. Записывается в следующем виде:

где x₀, y_0,z₀— координаты по соответствующим осям.

Таким образом, в данной статье были представлены основные сведения, которые могут понадобиться при решении задач на тему «Конус».

Источник

Геометрические тела. Конус.

Конус — геометрическое тело в евклидовом пространстве, которое можно получить путем объединения каждого луча, который исходит из одной точки (вершина конуса) и которые проходят через плоскую поверхность.

Бывает, конусом называется часть тела, которая имеет ограниченный объём и которая получена путем объединения каждого отрезка, которые соединяют вершину и точки плоской поверхности. Последняя, в таком случае, является основанием конуса, а конус называется опирающимся на данное основание.

Когда основание конуса является многоугольником – это уже пирамида.

Отрезки, которые соединяют вершину конуса и точки окружности основания, называют образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.

Прямой конус – это конус, в котором прямая, которая соединяет вершину конуса и центр основания, перпендикулярна плоскости основания.

Прямой круговой конус – это тело, которое получено вращением прямоугольного треугольника вокруг его катета как оси.

Высота конуса – это перпендикуляр, который опущен из вершины конуса на плоскость основания. Основание высоты в прямом конусе совпадает с центром основания.

Ось прямого кругового конуса – это прямая, которая содержит его высоту.

Сечение конуса плоскостью, который проходит через вершину конуса – это равнобедренный треугольник, боковые стороны этого треугольника являются образующими конуса.

Равнобедренным треугольником оказывается и осевое сечение конуса. Это сечение, проходящее через ось конуса.

Плоскость, которая параллельна основанию конуса и которая пересекает конус, отсекает от него конус меньшего размера. Оставшаяся часть является усеченным конусом.

Площадь боковой поверхности правильной n-угольной пирамиды, вписанной в конус:

То есть, площадь боковой поверхности конуса определяют с помощью формулы:

где R — радиус основания конуса, а l — длина образующей.

По тому же принципу: для площади боковой поверхности усеченного конуса с радиусами оснований R₁, R₂ и образующей l получаем такую формулу:

Прямой и косой круговой конусы с равным основанием и высотой. Эти тела обладают одинаковым объёмом:

Свойства конуса.

где S — площадь основания, H — высота.

Т.о., каждый конус, который опирается на это основание и имеющие вершину, которая находится на плоскости, параллельной основанию, имеют равный объём, так как их высоты одинаковые.

где α — угол раствора конуса.

а полная площадь поверхности (то есть сумма площадей боковой поверхности и основания), формула:

где R — радиус основания, l — длина образующей.

где S₁ и S₂ — площадь верхнего и нижнего оснований,

h и H — расстояния от плоскости верхнего и нижнего основания до вершины.

Источник

Конус

Прямой круговой конус.

Прямой и косой круговой конусы с равным основанием и высотой. Эти тела обладают одинаковым объёмом.

Усечённый прямой круговой конус.

Ко́нус (от др.-греч. κώνος «шишка») — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Если основание конуса представляет собой многоугольник, такой конус называется пирамидой.

Содержание

Связанные определения

Свойства

где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

где S₁ и S₂ — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, h и H — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

Уравнение конуса

где константы a, с определяются пропорцией Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность ). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz ) её уравнение имеет вид

Развёртка

Развёртка прямого кругового конуса

Источник

Что такое конус: определение, элементы, виды

В данной публикации мы рассмотрим определение, основные элементы и виды одной из самых распространенных фигур в пространстве – конуса. Представленная информация сопровождается соответствующими рисунками для лучшего восприятия.

Определение конуса

Далее мы будем рассматривать самый распространенный вид конуса – прямой круговой. Остальные возможные варианты фигуры перечислены в последнем разделе публикации.

Итак, прямой круговой конус – это трехмерная геометрическая фигура, полученная путем вращения прямоугольного треугольника вокруг одного из своих катетов, который в данном случае будет являться осью фигуры. Ввиду этого иногда такой конус называют конусом вращения.

Конус на рисунке выше получен в результате вращения прямоугольного треугольника ACD (или BCD) вокруг катета CD.

Основные элементы конуса

Между образующей конуса, его высотой и радиусом основания есть взаимосвязь (согласно теореме Пифагора):

Развёртка конуса – боковая поверхность конуса, развернутая в плоскость; является круговым сектором.

Примечание: Основные свойства конуса мы рассмотрели в отдельной публикации.

Источник