Что такое ось в алгебре
ОСЬ (в математике)
Смотреть что такое «ОСЬ (в математике)» в других словарях:
Ось в математике механике и физике — (l Ахе, die Axe). Слово это встречается весьма часто в математике, механике и физике. Хотя оно имеет разнообразные значения, но всегда с ним связано представление о симметрии. Представление о симметрии может быть различное: симметрия вокруг… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ОСЬ — в математике,1) ось координат прямая с указанными на ней направлением, началом отсчета и выбранной масштабной единицей, служащей для определения положения точек.2) Ось симметрии см. Симметрия … Большой Энциклопедический словарь
Ось (значения) — Ось (слово «ось» происходит от древнерусского «ость» долгий усик на плевеле каждого зерна колосовых растений или волос в пушном товаре) понятие некой центральной прямой, в том числе воображаемой прямой (линии): В технике:… … Википедия
Ось симметрии — Осевая симметрия тип симметрии, имеющий два несколько отличающихся определения: Отражательная симметрия. В математике (точнее, евклидовой геометрии) осевая симметрия вид движения (зеркального отражения), при котором множеством неподвижных точек … Википедия
Ось в технике — (l Axe, die Axe). Слово это встречается весьма часто в математике, механике и физике. Хотя оно имеет разнообразные значения, но всегда с ним связано представление о симметрии. Представление о симметрии может быть различное: симметрия вокруг… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Радикальная ось двух окружностей — Радикальная ось двух пересекающихся окружностей Радикальная ось двух окружностей геометрическое место точек … Википедия
Числовая ось — Числовая ось, или числовая прямая это прямая, на которой выбраны: некоторая точка O начало отсчёта; положительное направление, указанное стрелкой; масштаб для измерения длин. Между вещественными числами и числовой осью устанавливается … Википедия
Фокальная ось — Кривая второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида a11x2 + a22y2 + 2a12xy + 2a13x + 2a23y + a33 = 0, в котором по крайней мере один из коэффициентов отличен от нуля.… … Википедия
Координаты в математике — величины, определяющие положение точки. В Декартовых прямоугольных К. положение точки определяется тремя расстояниями ее от трех взаимно перпендикулярных плоскостей; пересечения этих плоскостей представляют собой три прямые, выходящие из одной… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Симметрия в математике — см. Ось … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Прямоугольная система координат. Ось абсцисс и ординат
Прямоугольная декартова система координат
Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
Координаты. Декартова система координат.
Координаты – совокупность данных, на основании которых точно характеризуется местоположение объекта.
Рене Декарт (1596–1650) предложил представлять местоположение точки на плоскости при помощи пары координат.
Для характеристики координат требуются ориентиры. Данными ориентирами на плоскости выступают две числовые оси. Сначала чертят горизонтальную ось, её принято определять как ось абсцисс и подписывать буквой х, указывают, что это ось 0х. Положительное направление на оси абсцисс принято слева на право и указывается стрелкой.
Следующей чертят вертикально ось, её принято определять как ось ординат и подписывать буквой у, указывают, что это ось 0у. Положительное направление на оси ординат принято снизу вверх и указывается стрелкой.
Оси пересекаются под углом 90°, то есть являются взаимно перпендикулярными. Точку их пересечения обозначают как «0». Точку «0» принято считать исходной точкой для отсчёта по каждой из осей.
Система координат — это две взаимно перпендикулярные координатные прямые, которые пересекаются в месте, являющемся началом отсчёта для каждой из них.
Координатные оси — это прямые, формирующие систему координат.
Ось абсцисс (0x) — расположенная горизонтально ось.
Ось ординат (0y) —расположенная вертикально ось.
Координатная плоскость — плоскость, в которой сформирована система координат. Для обозначения данной плоскости применяют x0y.
Цифры, указывающие числовые значения на осях размещают как по правую, так и по левую сторону от оси 0y. Цифры на оси 0x принято указывать внизу под осью.
Чаще всего единичные отрезки по оси 0y и оси 0x одинаковы. Но встречаются ситуации, когда они не равны друг другу.
Оси координат разделяют плоскость на 4 угла, которые обозначают как координатные четверти. Четверть, сформированная положительными полуосями (правый верхний угол), принято считать первой (I). Остальные четверти (координатные углы) располагаем против часовой стрелки.
Прямоугольная система координат
В повседневной жизни часто можно услышать фразу: «Оставь мне свои координаты». В ответ человек обычно оставляет свой адрес или номер телефона, то есть данные, по которым его можно найти.
Координаты могут обозначаться самыми разными наборами цифр или букв.
Например, номер автомобиля — это координаты, потому что по номеру машины можно определить из какого она города и кто ёё владелец.
Координаты — это набор данных, по которому определяется положение того или иного объекта.
Примерами координат являются: номер вагона и места в поезде, широта и долгота на географической карте, запись положения фигуры на шахматной доске, положение точки на числовой оси и т.д.
Всегда, когда мы по определенным правилам однозначно обозначаем какой-то объект набором букв, чисел или других символов, мы задаём координаты объекта.
Декартова система координат
Французкий математик Рене Декарт (1596–1650) предложил задавать положение точки на плоскости с помощью двух координат.
Для нахождения координат нужны ориентиры, от которых ведётся отсчёт.
Оси взаимно перпендикулярны (т.е. угол между ними равен 90° ) и пересекаются в точке, которую обозначают « O ». Точка « O » является началом отсчёта для каждой из осей.
Система координат — это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчёта для каждой из них.
Координатные оси — это прямые, образующие систему координат.
Ось абсцисс « Ox » — горизонтальная ось.
Ось ординат « Oy » — вертикальная ось.
Координатная плоскость — плоскость, в которой построена система координат. Обозначается плоскость как « x0y ».
Обращаем ваше внимание на выбор длины единичных отрезков по осям.
Цифры, обозначающие числовые значения на осях можно располагать как справа, так и слева от оси « Oy ». Цифры на оси « Ox », как правило, пишут внизу под осью.
Обычно единичный отрезок на оси « 0y » равен единичному отрезку на оси « 0x ». Но бывают случаи, когда они не равны друг другу.
Отсчитываем четверти (или координатные углы) против часовой стрелки.
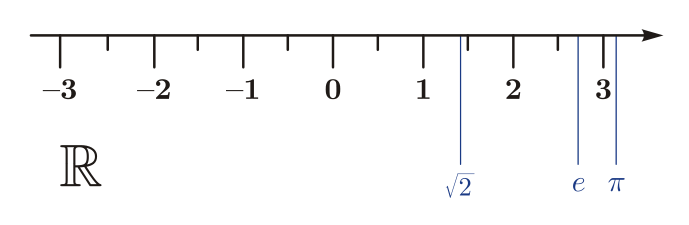
Числовая ось
Числовая ось, или числовая прямая — это прямая, на которой выбраны:
Между вещественными числами и числовой осью устанавливается взаимно однозначное соответствие: начало координат соответствует нулю, числовое значение произвольной точки соответствует расстоянию её до начала координат — в положительном направлении со знаком плюс, иначе — со знаком минус. [1] Таким образом, числовая ось состоит из точки начала координат и двух расходящихся от неё лучей, один из которых соответствует положительным, а другой — отрицательным числам. Естественный порядок точек на прямой при таком соответствии согласуется с упорядоченностью чисел.
Числовая прямая часто используется как наглядный образ множества вещественных чисел 
См. также
Примечания
Литература
Полезное
Смотреть что такое «Числовая ось» в других словарях:
Числовая прямая — Числовая ось, или числовая прямая это бесконечная прямая, на которой выбраны: некоторая точка O начало отсчета; положительное направление, указанное стрелкой; масштаб для измерения длин. Между вещественными числами и числовой осью… … Википедия
ЧИСЛОВАЯ ПРЯМАЯ — (числовая ось, координатная прямая, координатная ось) прямая, на которой изображают действительные числа и задают: точку О начало отсчёта, положительное направление (от О к А) и единичный отрезок (масштаб) ОА … Большая политехническая энциклопедия
ОСЬ — (1) в прикладной механике стержень, опирающийся на опоры и поддерживающий вращающиеся части машин (колёса вагонов) или механизмов (зубчатые колёса часов). В отличие от (см.) О. не передаёт полезного крутящего момента (см. (5)), а работает в… … Большая политехническая энциклопедия
Прямоугольная система координат — Прямоугольная система координат прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для… … Википедия
КОТАНГЕНС — одна из тригонометрических функций: другие обозначения: Область определения вся числовая ось, за исключением точек, абсциссы к рых К. функция неограниченная нечетная периодическая (с периодом ). К. и тангенс связаны соотношением Функция, обратная … Математическая энциклопедия
ПРИБЛИЖЕНИЕ ФУНКЦИЙ — замена по определенному правилу функции f(t).близкой к ней в том или ином смысле функцией j(t). из заранее фиксированного множества (приближающего множества). Предполагается, что функция f определена на том множестве Qm мерного евклидова… … Математическая энциклопедия
ТАНГЕНС — одна из тригонометрических функций: другие обозначения: tan, T, t. Область определения вся числовая ось, за исключением точек, абсциссы к рых функция неограниченная нечетная периодическая (с периодом Т. и котангенс связаны соотношением Функция,… … Математическая энциклопедия
Случайный элемент — обобщение понятия случайной величины. Термин был введён, по видимому, М.Фреше (1948), отмечавшим, что «развитие теории вероятностей и расширение области её приложений привели к необходимости перейти от схем, где (случайные) исходы опыта могут… … Википедия
Теория волн Эллиотта — (Elliott Wave Theory) Теория волн Эллиотта это математическая теория об изменении поведения общества или финансовых рынков Все о волновой теории Эллиотта: видео, книги, статьи о теории волн, информация о советниках и индикаторах волн Эллиотта… … Энциклопедия инвестора