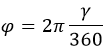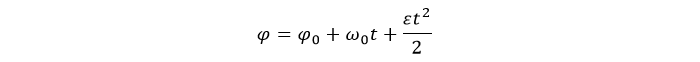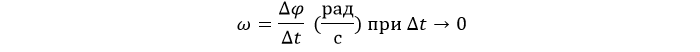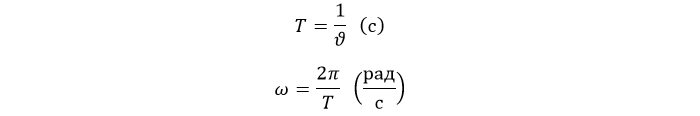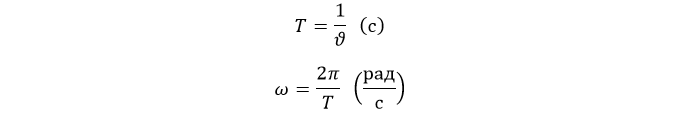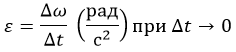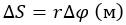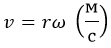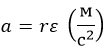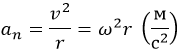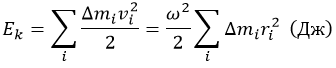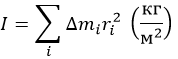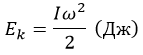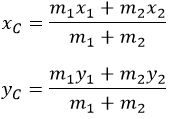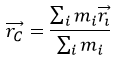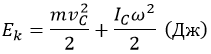Что такое ось вращения пример

Теоретическая механика

23. Вращательное движение твердого тела вокруг неподвижной оси.

Вращением твердого тела вокруг неподвижной оси называется такое движение твердого тела, при котором хотя бы две его точки остаются неподвижными.

Прямая, проходящая через эти неподвижные точки называется осью вращения.

Траекториями движения точек твердого тела являются окружности с радиусами равными расстояниям от заданных точек тела до оси вращения.

Уравнение вращательного движения твердого тела.

Величина называется угловым ускорением.

Частные случаи вращательного движения твердого тела.

Скорости и ускорения точек вращающегося твердого тел

При вращении твердого тела все его точки движутся по своим окружностям, центры которых лежат на оси вращения.

Определить число оборотов вала до остановки.

Поскольку один оборот равен радиан, число оборотов вала до остановки равно об.

Пример. Вал начинает вращаться равноускоренно из состояния покоя. В первые он совершает оборотов. Какова угловая скорость по истечении 5 секунд?

Теперь из уравнения (*) можно определить искомую угловую скорость при : (1/сек).

Источник

Вращательное движение твердого тела – движение, при котором все точки объекта описывают траекторию в виде окружности.

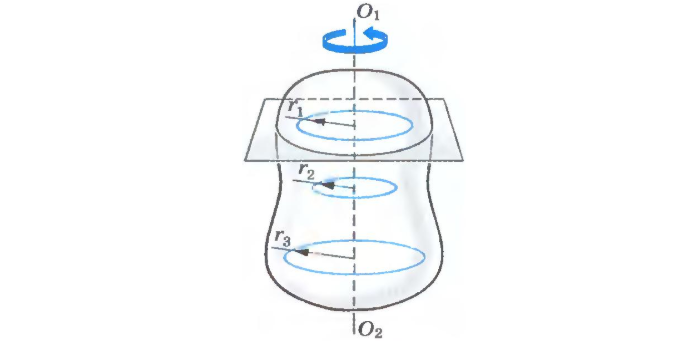
Распространенный случай в физике – вокруг покоящейся оси (рис. 1).

Рис. 1 Вращение твердого тела вокруг оси

Линия, соединяющая неподвижные точки, читается осью вращения. Кинематика перемещения в целом аналогична поступательной. Только путь измеряется не в метрах, а в радианах или градусах.

Последние связаны между собой следующей формулой:

ϕ – угол в радианах (рад);

γ – угол в градусах (°).

Закон и уравнение вращательного движения твердого тела

Законы движения также схожи. Для равноускоренного движения:

ϕ₀ – начальный угол (рад);

ω₀ – начальная угловая скорость (рад/с);

ε – угловое ускорение (рад/с 2 ).

Под положительным понимают перемещение против часовой стрелки.

Угловая скорость

В обычной жизни вращение оценивается в оборотах за единицу времени. За минуту чаще всего. Для расчетов такие характеристики неудобны. Поэтому определяется так:

Скорость в оборотах ν легко связать с угловой:

ν – скорость в оборотах (1/с).

Используется еще одна важная величина – период вращения T. За это время предмет совершает полный поворот:

Угловое ускорение

В уравнении движения был показан частный случай равноускоренного перемещения. Но это не всегда так. Также ε может принимать отрицательные значения в случае замедления.

Линейные величины

При малых величинах пройденный путь (см. рис. 2) будет равен:

где r – расстояние до центра вращения (м).

Откуда следует линейная скорость:

Вектор, перпендикулярный отрезку, r. То есть расположенный на касательной к окружности вращения.

И, соответственно, ускорение:

Кроме того, передвижение по кривой линии невозможно без центростремительного ускорения:

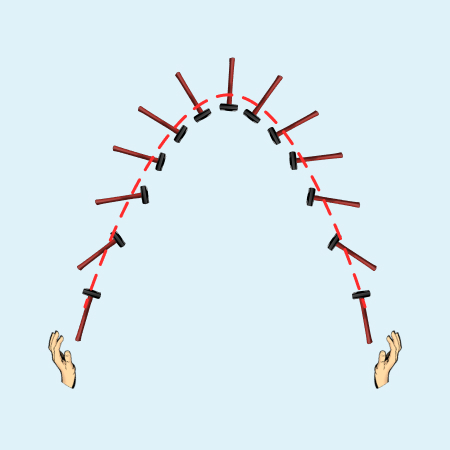
Возвратно-вращательное движение

Общий случай раскачивания маятника. Анализ подобных противоположных телодвижений пары объектов порождает некоторые парадоксы.

Возникают странные и дико звучащие названия вроде «безопорного движителя». Выводы в конечном итоге противоречат законам механики Ньютона.

Приверженцы таких рассуждений существуют и доводы имеют право на жизнь. Не все общепринятые взгляды безупречны. Евклидова геометрия тому пример. Теория довольно запутана, и здесь мы ее рассматривать не будем.

С учетом масс

Представив себе, что тело состоит из незначительных масс m_i, получим любопытные результаты. Кинетическая энергия выразится так:

Джоуль (Дж) – единица энергии и работы в системе СИ.

Моментом инерции относительно выбранной оси называется:

или в соответствующей интегральной форме.

Тогда энергия выразится следующим образом:

То есть имеется некий аналог массы. Но последняя является неизменной присущей объекту величиной. Момент же инерции зависит от местонахождения оси.

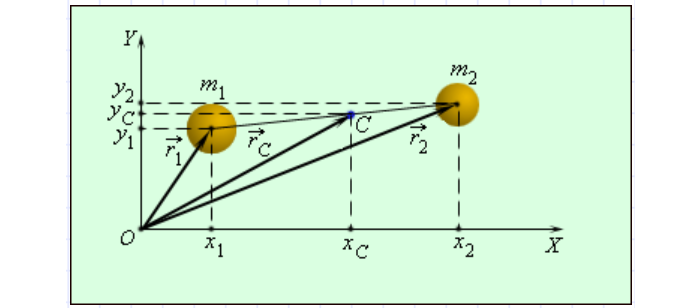
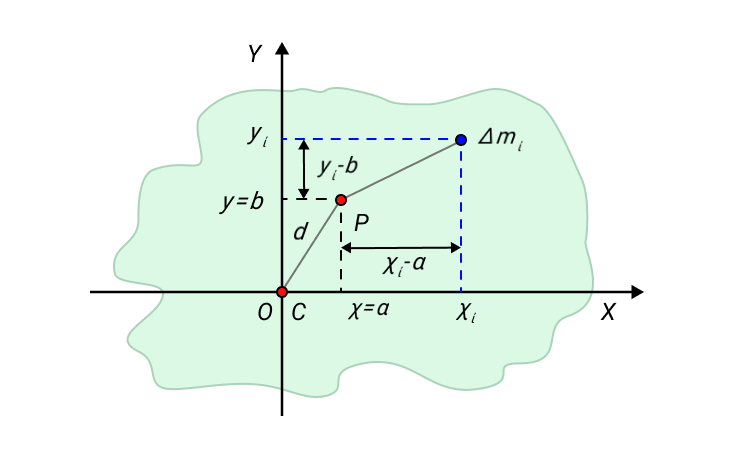
В реальных условиях распространен случай вращения вокруг оси, включающей центр масс. Найдем его для системы, указанной на рис. 3.

Рис. 3 Определение центра масс.

Определится по формулам:

Вектор, направленный из начала координат в центр масс, в общем случае выразится следующим образом:

Можно перевести в интегральную форму. В присутствии гравитации – заодно и центр тяжести.

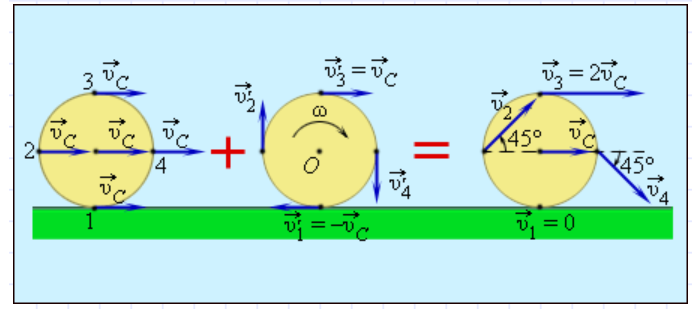
Можно сказать, что общее движение предмета включает поступательное и вращательное. Пример – качение чего-то округлого (рис. 4). При этом все перемещение точек можно исчерпывающе изобразить на рисунке. В таком варианте движение называется плоским.

Полная кинетическая энергия равна:

I_C – момент инерции относительно оси, включающей центр масс.

Рис. 4 Качение колеса

Частные случаи вращательного движения

1. Равномерное (рис. 5), с постоянной скоростью, с нулевым ускорением.

Выражается уравнением: φ = φ₀ + ωt

2. Равноускоренное. Рассмотрено ранее. Но все же уместны некоторые пояснения (рис. 6).

3. Вокруг неподвижной оси. Наиболее распространенный в рассмотрении вариант. Как для реальных нужд, так и в теории.

4. Возвратно-вращательное. В математическом выражении напоминает колебания. При подробном рассмотрении вызывает неудобные вопросы.

Заключение

Для разработчиков оборудования тема отнюдь не праздная. Рассматриваются задачи по передаче силового момента (в частности в ременных механизмах). Разбирается механика работы подшипников, гироскопов.

В артиллерии снаряды стабилизируются вращением. Да и расчеты их на прочность связаны со сложным напряженным состоянием в связи с раскручиванием в стволе.

Орбиты планет имеют отношение к рассматриваемой кинематике.

На самом деле все сферы использования данной темы невозможно перечислить, это действительно нужный раздел.

Источник

Ось вращения

Враща́тельное движе́ние — вид движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отчёта может быть как подвижной так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

Характеристики вращения

См. также

Ссылки

Смотреть что такое «Ось вращения» в других словарях:

ось вращения — прямая, неподвижная относительно вращающегося вокруг неё твердого тела. Для твердого тела, имеющего неподвижную точку (например, для детского волчка), прямая, проходящая через эту точку, поворотом вокруг которой тело перемещается из данного… … Энциклопедический словарь

ОСЬ ВРАЩЕНИЯ — прямая, неподвижная относительно вращающегося вокруг нее твердого тела. Для твердого тела, имеющего неподвижную точку (напр., для детского волчка), прямая, проходящая через эту точку, поворотом вокруг которой тело перемещается из данного… … Большой Энциклопедический словарь

ОСЬ ВРАЩЕНИЯ — мгновенная, у твёрдого тела, имеющего неподвижную точку (напр., у гироскопа), проходящая через эту точку ось, поворотом вокруг к рой тело перемещается из данного положения в положение к нему бесконечно близкое. Мгновенная О. в. непрерывно… … Физическая энциклопедия

ось вращения — — [В.А.Семенов. Англо русский словарь по релейной защите] Тематики релейная защита EN axis of revolutionaxis of rotation … Справочник технического переводчика

ось вращения — 3.17 ось вращения (axis of rotation): Прямая линия, проходящая через контрольную точку субъекта, вокруг которой может вращаться субъект, и лежащая в вертикальной плоскости симметрии. См. рисунок 1. Источник: ГОСТ Р ИСО 12124 2009: Акустика.… … Словарь-справочник терминов нормативно-технической документации

ось вращения — sukimosi ašis statusas T sritis automatika atitikmenys: angl. axis of revolution; axis of rotation; rotary axis; spin axis vok. Drehachse, f rus. ось вращения, f pranc. axe de rotation, m … Automatikos terminų žodynas

ось вращения — sukimosi ašis statusas T sritis fizika atitikmenys: angl. axis of rotation; rotation axis vok. Drehachse, f; Rotationsachse, f rus. ось вращения, f pranc. axe de rotation, m … Fizikos terminų žodynas

Ось вращения — мгновенная, у твёрдого тела, имеющего неподвижную точку (например, гироскопа), проходящая через эту точку ось, поворотом вокруг которой тело перемещается из данного положения в положение к нему бесконечно близкое; движение тела за… … Большая советская энциклопедия

ОСЬ ВРАЩЕНИЯ — прямая, неподвижная относительно вращающегося вокруг неё тв. тела. Для тв. тела, имеющего неподвижную точку (напр., для дет. волчка), прямая, проходящая через эту точку, поворотом вокруг к рой тело перемещается из данного положения в положение, к … Естествознание. Энциклопедический словарь

Ось вращения — прямая линия, неподвижная относительно вращающегося вокруг неё тела … Астрономический словарь

Источник

Вращение твердого тела

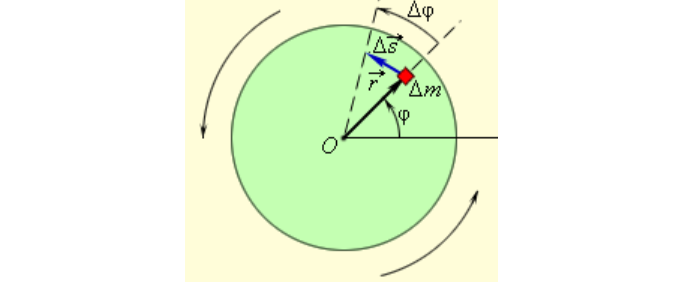
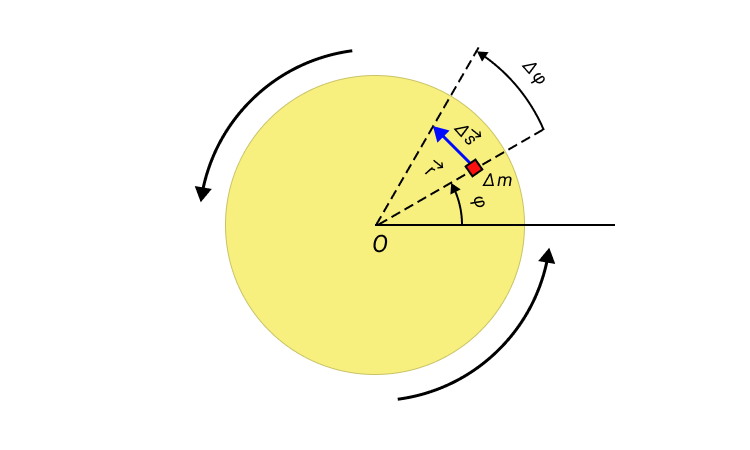
Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.

Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.

Если угловое перемещение Δ φ мало, то модуль вектора линейного перемещения ∆ s → некоторого элемента массы Δ m вращающегося твердого тела можно выразить соотношением:

Между модулями угловой и линейной скоростей можно установить связь посредством равенства

Модули линейного и углового ускорения также взаимосвязаны:

Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.

Модуль ускорения выражается формулой:

Физическая величина ∑ i ∆ m i r i 2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:

Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.

В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.

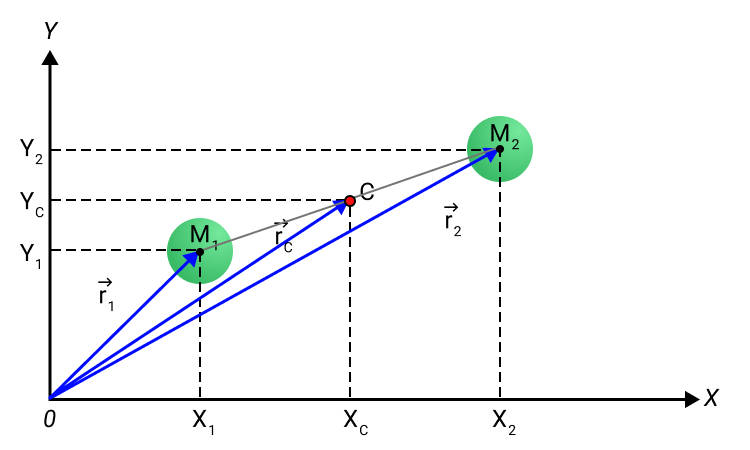
Рисунок 2. Центр масс C системы из двух частиц.

В векторной форме это соотношение принимает вид:

Аналогично, для системы из многих частиц радиус-вектор r C → центра масс определяется выражением

Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для r C → необходимо заменить интегралами.

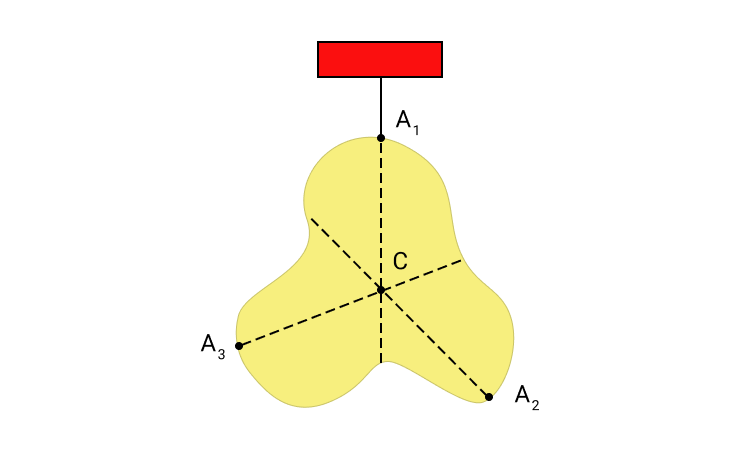
Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.

На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.

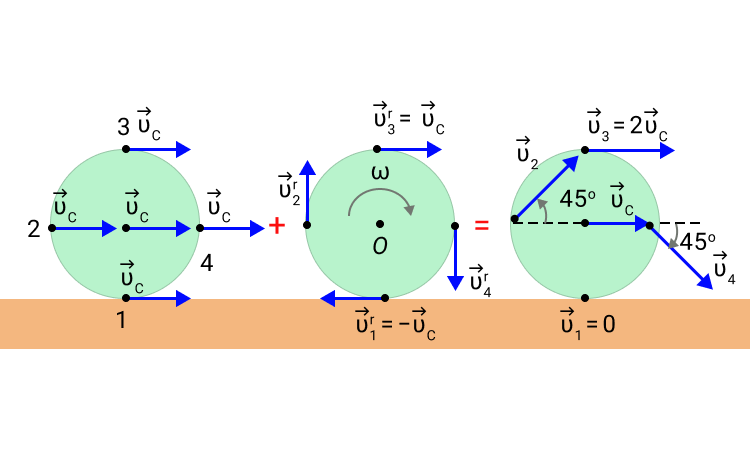
Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.

Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.

Теорема о движении центра масс

Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:

где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.

В механике используется теорема о движении центра масс.

Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.

На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.

Рисунок 5. Движение твердого тела под действием силы тяжести.

Теорема Штейнера о параллельном переносе оси вращения

Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.

Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.

По определению момента инерции:

Выражение для I P можно переписать в виде:

Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.

Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.

Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

где m – полная масса тела.

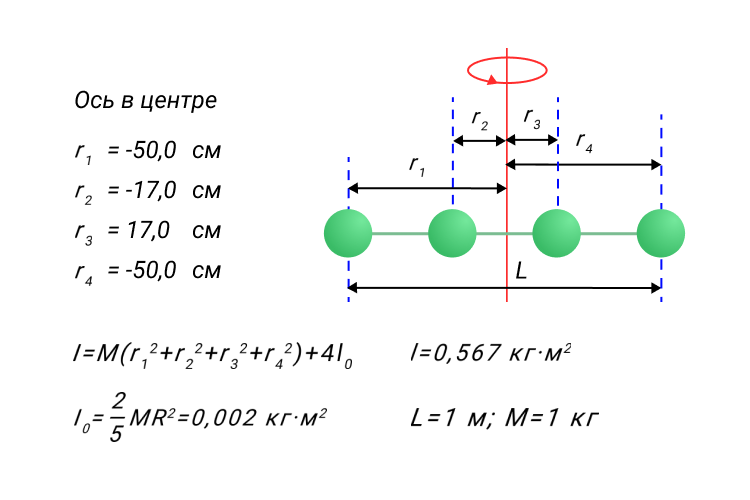
Рисунок 7. Модель момента инерции.

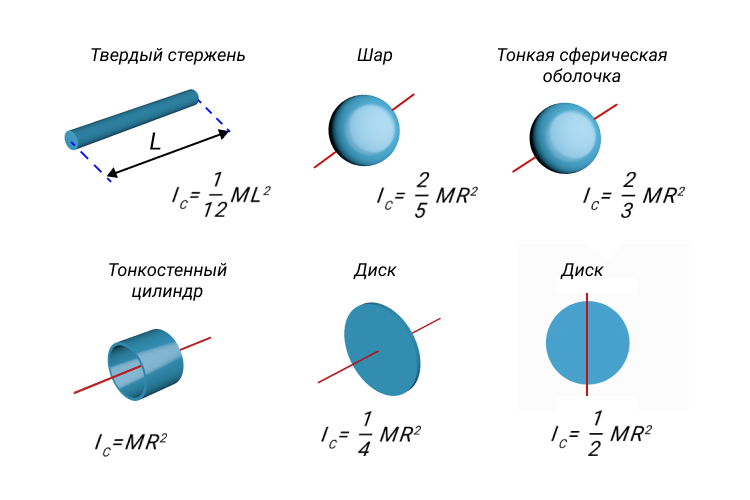
На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.

Рисунок 8. Моменты инерции I C некоторых однородных твердых тел.

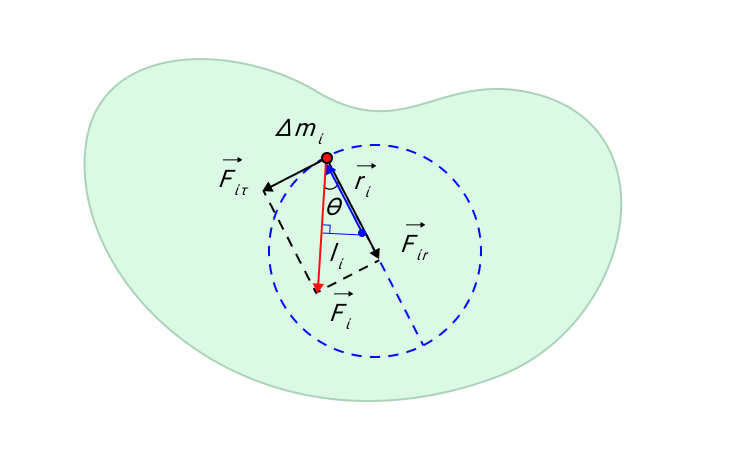
Основное уравнение динамики вращательного движения твердого тела

Рисунок 9. Касательная F i τ → и радиальная F i r → составляющие силы F i → действующей на элемент Δ m i твердого тела.

где ε = a i τ r i – угловое ускорение всех точек твердого тела.

Теперь нужно аналогичные соотношения записать для всех элементов массы Δm_i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.

Обычно за положительное направление вращения принимают направление против часовой стрелки.

Закон сохранения момента импульса

Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.

Так мы пришли к закону сохранения момента импульса.

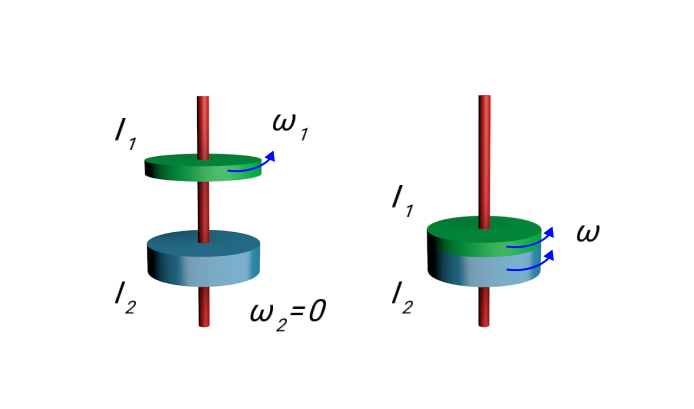
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.

Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.

Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.

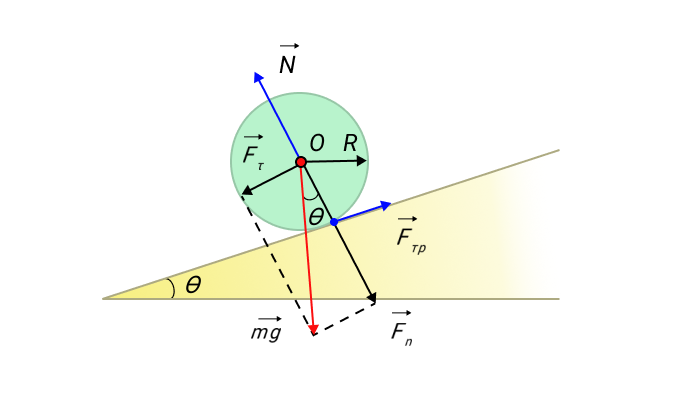
Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.

Рисунок 11. Качение симметричного тела по наклонной плоскости.

Уравнение вращательного движения:

Второй закон Ньютона для поступательного движения центра масс записывается в виде:

Источник

Вращательное движение – примеры, формула, понятие

Одним из наиболее часто встречающихся криволинейных движений является вращательное движение. Рассмотрим особенности такого движения подробнее.

Вращательное движение

Абсолютно твердое тело

Для описания вращательного движения нельзя использовать понятие материальной точки, поскольку оно предполагает, что все точки тела движутся одинаково.

При вращательном движении ситуация иная. Различные точки тела всегда движутся по-разному. Поэтому для вращательного движения вместо понятия «материальной точки» используется понятие «абсолютно твердого тела».

То есть такого тела, изменения размера и формы которого для данной задачи несущественны, все точки которого друг относительно друга можно считать неподвижными. По сути, абсолютно твердое тело – это система материальных точек, взаимные расстояния между которыми постоянны.

Рис. 1. Абсолютно твердое тело

Равномерное вращение абсолютно твердого тела

Вращением абсолютно твердого тела называют такое движение материальных точек, составляющих тело, при котором траектории движения точек представляют собой окружности с центрами, лежащими на одной прямой. Эта прямая называется «осью вращения», и как правило (но необязательно), проходит через само тело. При этом плоскости, в которых лежат траектории, параллельны между собой и перпендикулярны оси вращения. Примерами вращательного движения являются движение колес автомобиля, движение шестерен в механических часах, движение роторов электрических двигателей.

Рис. 2. Вращательное движение разных тел

При равномерном вращательном движении все точки тела поворачиваются на один и тот же угол за одно и то же время, поэтому скорость вращения измеряется в радианах в секунду:

Из этой формулы следует, что мгновенная линейная скорость точек тела тем больше, чем дальше расположена точка от оси вращения.

Центростремительное ускорение

Хотя при равномерном вращении модуль скорости каждой точки постоянен, его направление постоянно изменяется. Следовательно, вращение – это движение с ускорением, которое называется центростремительным. Такое название подчеркивает, что ускорение меняет не значение, а направление вектора скорости, и направлено оно всегда к центру вращения.

Рис. 3. Центростремительное ускорение

Модуль центростремительного ускорения равен:

Как можно видеть из формулы, центростремительное ускорение прямо пропорционально радиусу и квадрату частоты вращения. Если частота вращения тела будет высока, а предел прочности вещества тела недостаточен, вращающееся тело может быть разорвано. Так иногда происходит с некачественными отрезными дисками шлифовальной машины («болгарки»).

Что мы узнали?

Абсолютно твердое тело – это система материальных точек, взаимное расположение которых неизменно. Вращательное движение абсолютно твердого тела – это такое движение его точек, при которых траектории движения представляют окружности с центрами, лежащими на одной прямой – оси вращения.

Источник