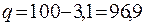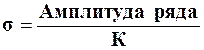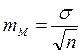Что такое ошибка репрезентативности

Что такое ошибка репрезентативности

Ошибка репрезентативности

Во-первых, как это ни парадоксально, это повышение точности данных уменьшение числа единиц наблюдения в выборке резко снижает ошибки регистрации. Правда, за счет неполноты охвата единиц возникает ошибка репрезентативности, т. е. представительности выборочных данных. Но даже взятые вместе ошибка наблюдения для выборки плюс ошибка репрезентативности обеспечивают большую точность выборочных данных по сравнению с массовым сплошным наблюдением. [c.156]

Фактическая ошибка репрезентативности [c.177]

Фактическая ошибка репрезентативности составляет [c.177]

После проведения выборки рассчитывают возможные ошибки выборочных показателей (ошибки репрезентативности), которые используются для оценки результатов выборки и для получения характеристик генеральной совокупности. [c.185]

Так как средняя величина имеет ошибку репрезентативности Ах, то можно считать, что итоговый подсчет в генеральной совокупности находится в пределах [c.188]

Оценку генерального параметра получают на основе выборочного показателя с учетом ошибки репрезентативности. В другом случае в отношении свойств генеральной совокупности выдвигается некоторая гипотеза о величине средней, дисперсии, характере распределения, форме и тесноте связи между переменными. Проверка гипотезы осуществляется на основе выявления согласованности эмпирических данных с гипотетическими (теоретическими). Если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных. Основой проверки статистических гипотез являются данные случайных выборок. При этом безразлично, оцениваются ли гипотезы в отношении реальной или гипотетической генеральной совокупности. Последнее открывает путь применения этого метода за пределами собственно выборки при анализе результатов эксперимента, данных сплошного наблюдения, но малой численности. В этом случае рекомендуется проверить, не вызвана ли установленная закономерность стечением случайных обстоятельств, насколько она характерна для того комплекса условий, в которых находится изучаемая совокупность. [c.193]

Расхождение между расчетным и действительным значением изучаемых величин называется ошибкой наблюдения. В зависимости от причин возникновения различают ошибки регистрации и ошибки репрезентативности. [c.21]

В отличие от ошибок регистрации ошибки репрезентативности характерны только для несплошного наблюдения. Они возникают потому, что отобранная и обследованная совокупность недостаточно точно воспроизводит генеральную совокупность в целом. [c.22]

Отклонение значения показателя обследованной совокупности от его величины в генеральной совокупности называется ошибкой репрезентативности. [c.22]

Ошибки репрезентативности также бывают случайными и систематическими. Случайные ошибки репрезентативности возникают, если отобранная совокупность неполно воспроизводит совокупность в целом. Величина этих ошибок может быть оценена. [c.22]

Систематические ошибки репрезентативности появляются вследствие нарушения принципов отбора единиц из исходной совокупности, которые должны быть подвергнуты наблюдению. Для устранения ошибок наблюдения необходимо осуществить контроль полученной информации. [c.22]

Степень варьирования оценивается дисперсией G 2, а ошибка репрезентативности [c.147]

Разность между результатами выборочного и сплошного наблюдения называется ошибками репрезентативности. На основе применения математики можно заранее рассчитать репрезентативность выборки информации, ее соответствие генеральной совокупности. [c.481]

Предельная ошибка выборки А= Л ц. Доверительное число t показывает, что расхождение не превышает кратную ему ошибку выборки. С вероятностью 0,954 можно утверждать, что разность между выборочной и генеральной не превысит двух величин средней ошибки выборки, т.е. в 954 случаях ошибка репрезентативности не выйдет за 2ц. [c.222]

Ошибки наблюдения подразделяются на два вида ошибки регистрации и ошибки репрезентативности. [c.36]

Ошибки репрезентативности возникают при несплошном обследовании в силу того, что состав отобранной для него части единиц совокупно- [c.36]

Ошибки репрезентативности. Основные проблемы выборочного наблюдения сводятся к тому, что при его применении могут возникать определенные ошибки. Следовательно, аудиторы вынуждены учитывать риски, свойственные выборочному наблюдению, а также знать, как необходимо минимизировать эти риски. Аудиторы называют это риском ошибочного принятия (непринятия) результатов выборки. При этом в аудиторской практике различают риски первого и второго рода для тестов системы контроля и проверки верности оборотов и сальдо по счетам [там же]. [c.49]

Случайные ошибки репрезентативности. Риск (опасность) возникновения этих ошибок проистекает из собственно случайных обстоятельств (типа арифметических ошибок при отсутствии контроля, описок и т.д.). Но мы сознательно оставляем в стороне и не анализируем здесь тривиальные ошибки наблюдения, которые выражаются, скажем, в описках и которые может допустить любой ассистент аудитора, осуществляющий выборку. [c.50]

Ошибка репрезентативности — разница между результатами выборочного и сплошного наблюдения. [c.546]

Выборочному обследованию свойственна некоторая погрешность в сравнении со сплошным, которая органически присуща вообще любому выборочному наблюдению. Указанная погрешность или ошибка носит название ошибки репрезентативности. [c.101]

Выборочной средней и выборочной доле свойственны, как указано выше, ошибки репрезентативности. Теория выборочного метода дает возможность определить средние этих ошибок. [c.102]

Сравнивая выборочную среднюю с генеральной средней, видим расхождение — 0,8 млн. руб. (11,6—10,8 = = 0,8). Это так называемая ошибка репрезентативности случайного бесповторного отбора. [c.106]

В среднем объем строительно-монтажных работ по этим трестам составил 10,6 млн. руб. Ошибка репрезентативности — 1,0 млн. руб. [c.107]

В среднем по 16 отобранным трестам объем строительно-монтажных работ составил 10,5 млн. руб. Ошибка репрезентативности 1,1 млн. руб. [c.108]

Выше разобраны пять основных способов отбора выборочной совокупности. Каждый из них имеет свою ошибку репрезентативности. Наименьшие ошибки репрезентативности получены при механическом отборе и при случайной выборке и наибольшая — при серийном отборе. В других случаях результаты могут получиться иные. В учебниках по статистике указывается, что теоретически наименьшая ошибка должна наблюдаться при типическом, затем при механическом отборах и случайной выборке. Наибольшая ошибка — при серийном отборе. [c.108]

Практически при пользовании выборочным методом остаются неизвестными ошибки репрезентативности, так как неизвестна бывает генеральная средняя. В связи с этим необходимо теоретически определить возможную величину этой ошибки. [c.108]

Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности. [c.22]

Ошибки репрезентативности также могут быть систематическими и случайными. Систематические ошибки репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором нарушается основной принцип научно организованной выборки — принцип случайности. Случайные ошибки репрезентативности означают, что, несмотря на принцип случайности отбора единиц, все же имеются расхождения между [c.22]

Разность между показателями выборочной и генеральной совокупности и будет случайной ошибкой репрезентативности. Ошибки репрезентативности [c.23]

При определении ошибки репрезентативности и объема выборки [c.16]

Как видно из приведенных расчетов, метод высшей и низшей точек довольно прост в применении. Его цель состоит в том, чтобы спрогнозировать поведение издержек при изменении деловой активности предприятия. Как и в любом прогнозе, здесь существует некоторая вероятность ошибки. Это связано с тем, что значение двух крайних показателей не всегда имеет репрезентативный характер. Поэтому из расчета следует исключать случайные, нехарактерные данные. [c.64]

Эта величина меньше предельной ошибки выборки, гарантированной с принятой доверительной вероятностью, 0,36

Источник

Определение ошибки репрезентативности (m)

Ошибка репрезентативности (m) показывает, насколько результаты полученные при выборочном исследовании, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования (генеральная совокупность).

Взаимосвязь объёма выборки и репрезентативности

· Репрезентативность не зависит от объема выборки. Репрезентативность достигается только тогда, когда в выборку отобраны объекты из разных групп, при условии, что их доли в генеральной и выборочной совокупности равны. Репрезентативность выборки зависит только от методики отбора единиц из генеральной совокупности в выборочную совокупность и не зависит от объема. Конечно, чем больше объем выборки, тем выше ее точность, однако, неверно распределенная выборка в 5000 единиц намного хуже, чем хорошо распределенная выборка в 500 единиц.

· Чем более однородна генеральная совокупность, тем меньший объем выборочной совокупности потребуется для получения точных результатов. Если, например, в генеральной совокупности все респонденты имеют одинаковый доход, то будет достаточно опросить одного респондента, чтобы узнать средний доход по совокупности. Чтобы определить вкус каши достаточно съесть одну ложку, а не всю тарелку, конечно, при условии, что каша хорошо перемешана.

При правильно составленной выборочной совокупности можно получить достаточно полное представление о закономерностях, присущих всей генеральной совокупности. Основным правилом составления выборочной совокупности является обеспечение ее репрезентативности, т.е. соответствия данных выборочной и генеральной совокупностей.

Выборочная совокупность должна быть представительной или репрезентативной (способность быть отражением генеральной совокупности), для чего необходимы следующие требования:

· обладать характерными чертами генеральной совокупности, т.е. по составу быть максимально похожей на неё;

· достаточной по объему, т.е. по числу наблюдений.

Формула ошибки репрезентативности (m) для относительных величин:

или , если число наблюдений менее 30 случаев,

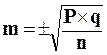
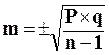
Р – величина показателя;

q=100–P, если показатель рассчитан на 100;

q=1000 –P, если показатель вычислен на 1000, и т.д.;

n – число наблюдений.

Например: работающих на предприятии – 1400 человек (n), имеющих гипертоническую болезнь (ГБ) – 44 человека.

Показатель заболеваемости ГБ

на 100 работающих, далее вычисляем по формуле

.

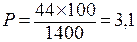
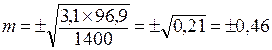
Вывод: результаты выборочной совокупности по определению ГБ на предприятии отличаются от генеральной совокупности на ± 0,46 (средняя ошибка ± 0,46).

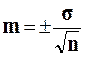
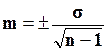
Формула (m) для средней величины: или , если число наблюдений меньше 30.

Например, у 49 больных (n) гастритом уровень пепсина М=1,0 г%, σ = ±0,35 г%

г%

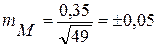
Вывод: результаты выборочной совокупности по определению уровня пепсина у 49 больных гастритом отличаются от генеральной совокупности (если бы исследования проводились у всех больных гастритом) на ± 0,05 (средняя ошибка ± 0,05).

Примечание: среднее квадратическое отклонение (σ)характеризует степень рассеивания вариант вокруг средней арифметической (смотри тему №3). Вычисляют по формуле:

Амплитуда ряда (см. тему №4)

К – «коэффициент К», (см. приложение №3).

Доверительные границы (М, P) средних и относительных величин –это границы относительных или средних величин размеров признака выход за пределы которых, вследствие случайных колебаний, имеет незначительную вероятность.

Доверительные границы для средней величины по формуле:

М_{ген., выб.} – доверительные границы средней величины генеральной и выборочной совокупности,

t – доверительный критерий (устанавливается исследователем, но должен быть не меньше 2, смотри ниже),

m – ошибка репрезентативности.

Доверительные границы для относительной величины по формуле:

P_{ген.,выб.} – доверительные границы относительной величины генеральной и выборочной совокупности;

t – доверительный критерий (устанавливается исследователем, но должен быть не меньше 2, смотри ниже);

m – ошибка репрезентативности.

Δ = tm (максимально возможная погрешность оценки генеральной совокупности),

t – доверительный критерий (устанавливается исследователем, но должен быть не меньше 2, смотри ниже);

m – ошибка репрезентативности.

Вероятность безошибочного прогноза (p) – это вероятность, с которой можно утверждать, что в генеральной совокупности относительных или средних величин (P, M) показатели будут находиться в пределах ±tm. Для медицинских исследований степень вероятности безошибочного прогноза (p) должна быть не менее 95%, т.е отображать объективную реальность проведенных исследований на 95%, тогда t=2 (см. ниже).

Зависимость доверительного критерия от степени вероятности безошибочного прогноза p (при n>30)

Источник

Определение ошибки репрезентативности

Определение средней ошибки средней (или относительной) величины (ошибки репрезентативности) — m.

Ошибка репрезентативности (m) является важнейшей статистической величиной, необходимой для оценки достоверности результатов исследования. Эта ошибка возникает в тех случаях когда требуется по части охарактеризовать явление в целом. Эти ошибки неизбежны. Они проистекают из сущности выборочного исследования; генеральная совокупность может быть охарактеризована по выборочной совокупности только с некоторой погрешностью, измеряемой ошибкой репрезентативности.

Ошибки репрезентативности нельзя смешивать с обычным представлением об ошибках: методических, точности измерения, арифметических и др.

По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном наблюдении, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования всех без исключения элементов генеральной совокупности.

Этот единственный вид ошибок, учитываемых статистическими методами, которые не могут быть устранены, если не осуществлен переход на сплошное изучение. Ошибки репрезентативности можно свести к достаточно малой величине, т. е. к величине допустимой погрешности. Делается это путем привлечения в выборку достаточного количества наблюдений (n).

Каждая средняя величина — М (средняя длительность лечения, средний рост, средняя масса тела, средний уровень белка крови и др.), а также каждая относительная величина — Р (уровень летальности, заболеваемости и др.) должны быть представлены со своей средней ошибкой — m. Так, средняя арифметическая величина выборочной совокупности (М) имеет ошибку репрезентативности, которая называется средней ошибкой средней арифметической (m_M) и определяется по формуле:

Как видно из этой формулы, величина средней ошибки средней арифметической прямо пропорциональна степени разнообразия признака и обратно пропорциональна корню квадратному из числа наблюдений. Следовательно, уменьшение величины этой ошибки при определении степени разнообразия (σ) возможно путем увеличения числа наблюдений.

На этом принципе основан метод определения достаточного числа наблюдений для выборочного исследования.

Относительные величины (Р), полученные при выборочном исследовании, также имеют свою ошибку репрезентативности, которая называется средней ошибкой относительной величины и обозначается m_P.

Для определения средней ошибки относительной величины (Р) используется следующая формула:

где Р — относительная величина. Если показатель выражен в процентах, то q = 100 – Р, если Р — в промиллях, то q=1000 – Р, если Р—в продецимиллях, то q=10 000 – Р и т.д.; n — число наблюдений. При числе наблюдений менее 30 в знаменатель следует взять n – 1.

Примеры определения средних ошибок
средних и относительных величин

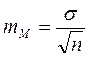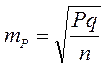У 49 больных гипертиреозом исследован уровень пепсина n=49 M=1.0 г% σ=0,35 г% mM=?	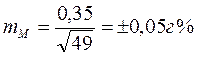Исследовано 110 больных с абсцессом легкого, из них у 44 обнаружены дистрофические изменения пародонта n=110 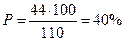лиц с дистрофическими изменениями пародонта q=100 – 40=60% лиц без дистрофических изменений пародонта mP=?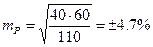

Каждая средняя арифметическая или относительная величина, полученная на выборочной совокупности, должна быть представлена со своей средней ошибкой. Это дает возможность рассчитать доверительные границы средних и относительных величин, а также определить достоверность разности сравниваемых показателей (результатов исследования).

Источник

Репрезентативность выборочных данных

Репрезентативность — важнейшее свойство данных, используемых для построения аналитических моделей. Независимо от того, в какой предметной области и какими методами производятся выборочные исследования, отсутствие репрезентативности выборки приводит к некорректным результатам. В статье рассказываем подробнее об этом важном свойстве.

Репрезентативность — важнейшее свойство данных, используемых для построения аналитических моделей. Оно отражает способность данных представлять зависимости и закономерности исследуемой предметной области, которые должна обнаружить и научиться воспроизводить построенная модель. Иными словами, репрезентативность показывает, содержат ли анализируемые данные достаточно информации для построения качественной модели, а так же, может ли эта информация быть использована алгоритмом построения модели.

Репрезентативность генеральной совокупности отражает способность совокупности описывать существенные свойства, зависимости и закономерности объектов, процессов и явлений предметной области. Она достигается за счёт правильной организации сбора и консолидации первичных данных.

Репрезентативность выборки описывает способность выборочных данных отражать структурные свойства совокупности, из которой они были извлечены. Т.е. даёт ответ на вопрос: можно ли в исследовании заменить совокупность на выборку без значимого ухудшения результатов анализа. Репрезентативность выборки достигается с помощью правильного выбора метода сэмплинга.

Таким образом, репрезентативность выборки касается только воспроизведения характеристик совокупности. Если сама исходная совокупность плохо представляет предметную область, то, даже если полученная из неё выборка будет репрезентативной, построить на её основе корректную с точки зрения предметной области модель будут невозможно.

Например, пусть компания собирается вывести на рынок новый продукт. При этом она хочет провести маркетинговые исследования в виде опроса клиентов о желаемых характеристиках и параметрах продукта. Число клиентов компании насчитывает сотни тысяч человек (генеральная совокупность), поэтому опросить их всех не представляется возможным физически, не является целесообразным экономически.

Поэтому компания формирует выборку клиентов для проведения опроса. Если мнение клиентов из выборки отражает мнение большинства клиентов и может быть использовано для принятия решений о параметрах и характеристиках нового продукта, то такая выборка будет репрезентативной.

Независимо от того, в какой предметной области и какими методами производятся выборочные исследования, отсутствие репрезентативности выборки приводит к некорректным результатам. Поэтому в процессе анализа необходимо убедиться, что сформированная выборка репрезентативна.

Таким образом, репрезентативная выборка — это такая выборка, в которой представлены все подгруппы, важные для исследования. Помимо этого, характер распределения рассматриваемых параметров в выборке должен быть таким же, как в генеральной совокупности.

Особенно важным является обеспечение репрезентативности в машинном обучении, для построения моделей классификации и регрессии используется несколько выборок: обучающая, тестовая и валидационная, которые тем или иным способом отбираются из исходного набора данных. И все эти выборки должны быть репрезентативными.

Обеспечение репрезентативности

В основе построения репрезентативной выборки лежит правильный выбор используемого алгоритма сэмплинга. При этом размер выборки, хотя и является важным, сам по себе не гарантирует ее репрезентативности. Например, интернет-опрос может показать, что 100% людей пользуется интернетом, хотя это не соответствует действительности (т.е. репрезентативность нарушена).

Выделяют качественную (структурную) и количественную репрезентативность.

Рисунок 1. Количественная и качественная репрезентативность

Качественная репрезентативность

Качественная репрезентативность показывает, что все группы, присутствующие в совокупности, будут представлены и в выборке. Для этого каждый элемент совокупности должен иметь равную вероятность, быть выбранным, а сама выборка должна производиться из однородных групп.

Наиболее оптимальным способом формирования репрезентативной выборки является простой случайный сэмплинг, поскольку в этом случае у любого представителя генеральной совокупности будет одинаковая вероятность попасть в выборку.

Например, при формировании выборки клиентов для опроса, в нее попадут люди из различных социальных групп пропорционально их долям в генеральной совокупности. В результате, выборка будет представлять собой уменьшенную копию генеральной совокупности.

Случайность отбора респондентов в выборку может обеспечивается различными методами. Например, для опроса клиентов берутся номера клиентских карт, которые случайным образом отбираются компьютерной программой с использованием генератора случайных чисел.

Однако, на практике применить простой случайный сэмплинг не всегда представляется возможным. Это связано с тем, что генеральная совокупность может быть неоднородной и будет содержать группы объектов.

Например, если опрос будет проводиться по телефону, то большинство откликов будет получено от пенсионеров, как людей менее занятых и более склонных идти на контакт. Очевидно, что если опрос проводится о продукте, ориентированном на молодёжь, то ценность мнения пенсионеров вряд ли будет высокой.

Чтобы решить эту проблему, можно использовать случайный стратифицированный сэмплинг, когда исходная совокупность сначала разделяется на слои (страты) по некоторому признаку. Например, клиенты могут быть стратифицированы по возрасту. Тогда страты могут быть сформированы пропорционально доле объектов в группах, что позволит уменьшить или увеличить долю той или иной группы, сохранив репрезентативность.

Другой вариант — использовать кластерный (групповой) сэмплинг, когда клиенты предварительно разбиваются на качественно однородные группы — кластеры, и отбор производится из каждого кластера независимо. При этом вероятность отбора может быть одинаковой для всех кластеров, или различной. Можно некоторые кластеры вообще исключить из отбора. В нашем примере клиенты могут быть разбиты на кластеры по социальному статусу — студенты, работающие, пенсионеры, военнослужащие и т.д. Таким образом, долю, пенсионеров в выборке, можно уменьшить или совсем исключить.

Количественная репрезентативность

Количественная репрезентативность показывает, является ли достаточным число элементов выборки для представления характеристик генеральной совокупности с заданной погрешностью. Например, при неизвестной величине генеральной совокупности, когда результат отражается в виде показателя относительной доли, число элементов выборки, обеспечивающее количественную репрезентативность, может быть вычислено по формуле:

где t — доверительный коэффициент, показывающий, какова вероятность того, что размеры показателя не будут выходить за границы предельной ошибки, p — доля единиц наблюдения, обладающих изучаемым признаком, q=1−p — доля единиц наблюдения, не обладающих изучаемым признаков, Δ — допустимая ошибка выборки.

n=\frac<2^<2>\cdot 0,25\cdot 0,75><0,05^<2>>=300 заёмщиков.

Если же показатель — не относительная средняя величина просроченной задолженности по всем клиентам, то число наблюдений будет:

Если используется выборка без возврата и размер генеральной совокупности известен, то для определения необходимого размера случайной выборки при использования относительных величин (долей) применяется формула:

n=\frac\cdot p\cdot q\cdot N><\Delta ^<2>\cdot N+t^<2>\cdot p\cdot q>

где N — число наблюдений генеральной совокупности. Для средних значений исследуемой величины формула примет вид:

n=\frac<2^<2>\cdot 0,25\cdot 0,75\cdot 500><0,05^<2>\cdot 500+2^<2>\cdot 0,25\cdot 0,75>\approx 188 клиентов.

Таким образом, необходимый объем выборки при безвозвратном отборе меньше, чем при возвратном (соответственнo, 188 и 300).

В целом, число наблюдений, требуемое для получения репрезентативной выборки, изменяется обратно пропорционально квадрату допустимой ошибки.

Методы оценки репрезентативности

Формально, выборку называют репрезентативной, когда результат оценки определенного параметра по данной выборке совпадает с результатом, оцененным по генеральной совокупности с учетом допустимой погрешности (ошибки репрезентативности). Если выборочная оценка отличается от оценки по генеральной совокупности более, чем на заданный уровень погрешности, то такая выборка считается нерепрезентативной.

Репрезентативность оценивается по отдельным параметрам выборки и совокупности. При этом выборка может оказаться репрезентативной по одним параметрам и нерепрезентативной по другим. Поэтому говорить о репрезентативности как о дихотомическом свойстве выборки (репрезентативна или нерепрезентативна) было бы не верно: выборка может одни параметры генеральной совокупности воспроизводить более точно, а другие — менее. Поэтому правильнее говорить о мере репрезентативности определённой выборки по конкретным параметрам.

Основным моментом в определении репрезентативности выборки является обоснование погрешности, в пределах которой выборка признается репрезентативной. Одна и та же выборка может быть достаточно репрезентативной для одной задачи и недостаточно для другой. Кроме этого, нужно проверять репрезентативность выборки по параметрам, имеющим существенное значение для предметной области исследования. Например, в маркетинговых исследованиях для анализа клиентов важны пол, возрасту, образование и пр.

Следует отметить, что далеко не все задачи бизнес-аналитики требуют строгого статистического подтверждения репрезентативности выборок. Как правило, это задачи точного прогнозирования. Что касается обычных задач, связанных, например, с определением предпочтений действующих и потенциальных клиентов, то они решаются охватом типичной клиентуры, которую можно найти непосредственно в торговых центрах.

Статистические методы

Данные, полученные в результате выборочных обследований, являются реализациями случайных величин (возраст, стаж работы, доход и т.д.). Обычно, на практике считают, что выборка является репрезентативной, если её статистические параметры (среднее значение, дисперсия, среднеквадратичное отклонение и т.д.) отличаются от параметров совокупности не более, чем на 5%.

Однако, данный подход применим только при условии, что вся генеральная совокупность известна и для неё можно вычислить статистические характеристики. Но на практике такое встречается редко, поскольку часть потенциально интересных для исследования объектов оказывается недоступной для наблюдения.

В этом случае прибегают к формированию двух независимых выборок, вычисляют и сравнивают их характеристики, и если они совпадают (не различаются значимо), то выборки считаются репрезентативными. В теоретическом плане такой подход является достаточно привлекательным, однако, на практике сложно реализуем. Во-первых, формирование нескольких выборок ведёт к дополнительным затратам, а во-вторых, если параметры выборок значимо различаются, то невозможно сказать, какая из них репрезентативна.

Нестатистические методы

Статистические методы оценки репрезентативности выборочных данных, хотя и являются строго обоснованными, но довольно сложны в использовании (особенно для пользователей, не имеющих достаточной математической подготовки). Кроме этого они могут иметь ограничения (например, независимость выборок), удовлетворить которым достаточно сложно.

Статистические подходы к оценке репрезентативности выборок имеет смысл использовать, если для анализа данных используются статистические методы. Методы машинного обучения, которые является эвристическими и в большинстве случаев не обеспечивают точного и единственного решения, вообще говоря, не нуждаются в точной оценке репрезентативности обучающих выборок. Поэтому в них используются свои техники для определения того, насколько обучающая или тестовая выборка хорошо представляют исходную совокупность.

Ещё одной особенностью выборок, используемых в машинном обучении, является то, что объём исходной совокупности, из которой формируются обучающее, тестовое, а при необходимости, и валидационное множество, известен, поскольку данные содержатся в консолидированных таблицах источника данных.

Затем вычислим величину:

где D_<_> — общее расстояние по всей совокупности, N — число наблюдений совокупности.

Тогда индекс ближайшего соседа будет:

Если значение данного показателя близко к 1, то точки выборки имеют равномерное пространственное распределение. Если меньше 1, то пространственное распределение точек неоднородно. Если NNI больше 1, то имеет место значительная дисперсия значений внутри выборки.

Очевидно, что наилучшим вариантом с точки зрения репрезентативности будет первый случай, когда пространственное распределение точек данных в совокупности и выборке примерно одинаковое. Второй случай показывает, что внутри выборки могут присутствовать некоторое локальные особенности, нехарактерные для всей совокупности.

В литературе можно найти больше количество разнообразных алгоритмов и методов оценки репрезентативности выборок для машинного обучения, разработанных для различных предметных областей исследования и типов задач анализа. Большинство их них являются эвристическими и не гарантируют получения наилучшего результата. Поэтому самым надёжным критерием репрезентативности выборки, на основе которой строилась определённая обучаемая модель, является точность и обобщающая способность самой модели.

Ремонт выборки

Возникает вопрос: а что делать в ситуации, когда аналитику доступна только выборка «как есть», а её репрезентативность неудовлетворительная? При этом доступ к генеральной совокупности для формирования более репрезентативной выборки у него отсутствует (например, из-за проблем с сетью, невозможности повторных исследований из-за высоких затрат и т.д.). В этом случае улучшить ситуацию может специальная процедура, которая называется «ремонт выборки».

Все действия аналитика, связанные с репрезентативностью, можно разделить на два этапа: контроль и ремонт.

Контроль и ремонт выборки рассматриваются как обязательные этапы любого выборочного исследования. Хотя, некоторые авторы не разделяют эти два этапа, а включают ремонт в общую процедуру контроля выборки. Ряд вопросов, связанных с контролем выборки был рассмотрен выше.

Основной целью ремонта является повышение качества выборки в смысле отражения ею зависимостей и закономерностей исследуемых процессов и явлений, которые требуется обнаружить в процессе анализа. При этом не следует путать ремонт выборки с повышением качества данных вообще.

Ремонт выборки, обычно, включает следующие задачи:

Следует отметить, что единого, строго обоснованного подхода к ремонту выборок, вообще говоря, не существует, хотя в литературе можно встретить некоторые общие рекомендации. В большинстве практических случаев аналитику приходится самостоятельно выбирать, какие преобразования следует применить к выборке для повышения её репрезентативности.

Источник