Что такое основание классификации множества
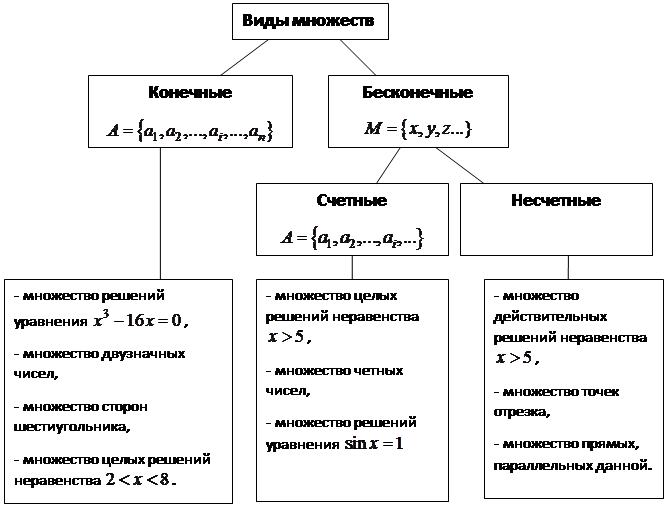
Классификация множеств



Основной характеристикой множеств является количество элементов, содержащихся в этом множестве.
По данному признаку выделяются:
1. Множество, содержащее конечное число элементов называется конечным.
Количество элементов конечного множества называют его мощностью.
2. Множество, не являющееся конечным, называется бесконечным.
3. Если множество не содержит элементов, то оно называется пустым и обозначается 
1. Конечное множество по признаку мощностихарактеризуется:
Два множества А и В называются эквивалентными, или, равномощными, если между их элементами можно установить взаимно-однозначное соответствие.
Пример: Рассмотрим множества, состоящие из букв слов:




Множества А, В и С имеют равные мощности: 

При этом, множества А и В равны, а множества А и С – эквивалентны.
Эталоном для сравнения множеств служит натуральный ряд чисел. Поэтому все числовые последовательности, содержащие различные элементы, эквивалентны натуральному ряду чисел, что видно по их индексам.
2. Бесконечное множество, которое эквивалентно множеству натуральных чисел, называется счетным.
Говорим, что все элементы счетного множества пронумерованы.
В противном случае бесконечное множество будет несчетным.
В 1878 году Георг Кантор доказал, что множество точек, расположенных на отрезке от 0 до 1 несчетно.
Во множестве могут быть выделены подмножества.
Если каждый элемент множества K принадлежит множеству М, то множество К называют подмножеством множества М и обозначают 
1) множество всех книг данного автора в библиотеке, есть подмножество всех книг в библиотеке.
2) множество студентов, обучающихся на «4» и «5» в группе есть подмножество всех студентов группы.
3) 

Пустое множество является подмножеством любого множества.
Количество подмножеств для исходного множества может быть рассчитано.
Для этого познакомимся с термином булеан.
Булеаноммножества М (N(M)) называется множество всех его подмножеств.
Рассмотрим множество 












Подмножества 

остальные – 2-15 – это собственные подмножества.
Всего мы нашли 16 различных подмножеств множества М. Это число 16 может выразить: 
В общем случае, для любого конечного множества, состоящего из n элементов, число возможных подмножеств равно 
Множество U, состоящее из всех возможных элементов, обладающих данным признаком, называется универсальным.
Вопрос 2. Операции над множествами
И свойства операций
Множества изображаются при помощи диаграмм Эйлера-Венна (круги на плоскости).
Элементы множества изображаются точками:
— внутри круга, если они принадлежат данному множеству;
— вне круга, если не принадлежат.



Основными операциями над множествами являются операции:
— пересечение,
— объединение,
— разность,
1. Пересечением множеств А и Вназывается множество 
Пример: Если 


При помощи диаграмм Эйлера-Венна пересечение множеств изображается следующим образом:
2. Объединением множеств А и Вназывается множество 
Пример: Если 


При помощи диаграмм Эйлера-Венна объединениемножеств изображается следующим образом:
3. Разностью множеств А и В называется множество 
Пример: Если 



По диаграмме видно, что 

4. Симметрической разностью А и Вназывается множество 
Пример: Если 


При помощи диаграмм Эйлера-Венна симметрическая разность множеств изображается следующим образом:
5. Дополнением множества А до множества U называется множество 

Свойства операций
Операции над множествами обладают рядом свойств, похожих на свойства операций сложения и умножения чисел.
| Объединение (сложение) | Пересечение (умножение) |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 , ,  |  , ,  |
 , ,  |  , ,  |
Используя эти операции можно выражать одни множества через другие, при этом сначала выполняется операция дополнения, затем пересечения и только затем операции объединения и разности. Для изменения порядка в выражении используют скобки.
Пример. Доказать справедливость следующего равенства и проверить результат на диаграмме Эйлера-Венна: 
Решение. Преобразуем по очереди левую и правую части данного равенства:
1) 
2)

Использовали переход от разности к пересечению, закон де Моргана, свойство дистрибутивности, свойство 

После преобразования видно, что левая и правая части равенств одинаковые, следовательно, равенство доказано.
Проверим равенство на диаграмме Эйлера-Венна.
Понятие разбиения множества на классы
Понятие множества и операций над множествами позволяют уточнить представление о классификации.
Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.
Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.
Любая классификация связана с разбиением некоторого множества объектов на подмножества.
Считают, что множество Х разбито на классы Х


1) подмножества Х


2) объединение этих подмножеств совпадает с множеством Х.
Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.
Например: а) Множество треугольников Х разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством Х; b) Из множества треугольников Х выделили подмножества равнобедренных, равносторонних и разносторонних треугольников. Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества Х на классы мы не получили.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Нас интересуют числа со свойством «быть кратным 3». Это свойство позволяет выделить из множества N подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества N. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством N, то имеем разбиение данного множества на два класса.
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, свойства натуральных чисел: «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N можно выделить два подмножества: А – множество чисел, кратных 3 и В – множество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Разбиения на подмножества А и В в данном случае на произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей. Каждая область изображает некоторое подмножество множество N. Множество I состоит из чисел, кратных 3 и 5, множество I – из чисел, кратных 3 и не кратных 5, множество III – из чисел, кратных 5 и не кратных 3, множество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех множеств есть множество N.

Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается
на три класса (рис. 14): I – класс чисел, кратных 6; II – класс чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.
Что такое основание классификации множества
2.2. Классификация множеств. Подмножества
Для дальнейшего изучения множеств попытаемся дать некоторую их классификацию. Прежде всего, множества можно разделить на конечные и бесконечные.
В математике приходится сталкиваться и с другими – не конечными, или, как принято говорить, с бесконечными множествами. Множество называется бесконечным, если оно состоит из бесконечного числа элементов. Таковы, например, множество всех натуральных чисел, множество точек окружности, множество прямых, проходящих через точку плоскости и т.д.
Пустым множеством является и множество корней системы уравнений:
Без введения пустого множества мы не могли бы, скажем, говорить о множестве корней произвольного уравнения, не убедившись предварительно, что данное уравнение имеет хотя бы один корень. Существование этого понятия сокращает и упрощает формулировки многих теорем, облегчает введение новых понятий.
Если каждый элемент множества В является также и элементом множества А, то говорят, что множество В называется подмножеством множества А.
Обозначатся это следующим образом: В Í А ( В включено в А).
Например, < 2, 4 >Í < 2, 3, 4, 5 >. Множество пешек в шахматах является подмножеством шахматных фигур, множество квадратов – подмножеством прямоугольников, множество отличников 101 группы – подмножеством студентов этой группы.
Если в множествах А и В отличаются хотя бы одним элементом, то А ¹ В.
Можно заметить, что само множество А является подмножеством самого себя:
Действительно, по определению подмножества каждый элемент множества А является элементом множества А. Это свойство множества называют рефлективностью.
Кроме того, пустое множество, по определению, считают подмножеством любого множества:
В этом случае множество I называют универсальным множеством. Например, для алгебры универсальным множеством является множество действительных чисел. Если мы рассматриваем множества точек на плоскости, то универсальным будет множество всех точек на плоскости.
Таким образом, у любого множества обязательно существуют хотя бы два подмножества: пустое множество и само множество. Эти два подмножества называются несобственными подмножествами. Любое подмножество, отличное от несобственного, называется собственным подмножеством данного множества.
Кроме свойств (2.1) и (2.2) выделяют следующие свойства отношения включения:
Множество А называется истинным подмножеством множества В, если А 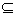
Так, < 2, 4 >Ì < 2, 3, 4, 5 >. Множество пешек в шахматах также будет истинным подмножеством шахматных фигур, а вот множество отличников 101 группы может, чисто теоретически, совпадать с множеством студентов 101 группы.
Для истинных подмножеств также выполняется свойство транзитивности: если А