Что такое основное свойство алгебраической дроби
Основное свойство алгебраической дроби: формулировка, доказательство, примеры применения.
Раньше, изучая тему обыкновенные дроби, мы уже встречались с основным свойством дроби. Но в то время мы его сформулировали в «упрощенной» форме, удобной и достаточной для работы с обыкновенными дробями. В этой статье мы взглянем на основное свойство дроби применительно к алгебраическим дробям (то есть, к дробям, числителем и знаменателем которых являются многочлены, в некоторых учебниках алгебры такие дроби называют не алгебраическими, а рациональными дробями). Сначала сформулируем основное свойство алгебраической дроби, обоснуем его, а после этого перечислим основные области его применения.
Навигация по странице.
Формулировка и обоснование
Фактически про деление числителя и знаменателя на число можно не говорить – этот случай покрывается равенством вида 
. Например, равенство 
можно обосновать через деление с использованием равенства 
как 
, но его же можно обосновать и на основании равенства как 
. Поэтому дальше мы будем ассоциировать основное свойство дроби с равенством (и 
), и не будем останавливаться на равенстве (и 
).
Справедливость основного свойства алгебраической дроби вытекает из того, что действия с многочленами вводились в полном согласии с соответствующими действиями с числами.
Сферы применения основного свойства алгебраической дроби
Пришло время разобраться с практическим применением основного свойства алгебраической дроби. Оно применяется, в основном, для проведения двух следующих преобразований алгебраических дробей – приведения к новому знаменателю и сокращения алгебраических дробей. Обговорим, в чем они заключаются.
Наиболее часто приведение к новому знаменателю приходится выполнять при сложении и вычитании алгебраических дробей.
Стоит отметить, что если алгебраическая дробь имеет дробные коэффициенты, то умножение ее числителя и знаменателя не некоторое число позволяет перейти к целым коэффициентам, и тем самым упростить ее вид. К примеру, 
. А на умножении числителя и знаменателя на минус единицу основаны правила изменения знаков у членов алгебраической дроби.
Понятие алгебраической дроби. Основное свойство
Определение алгебраической дроби
Чтобы дать определение алгебраической дроби, необходимо повторить, что такое алгебраическое выражение (см. §1 справочника для 7 класса) и многочлен (см. §14 справочника для 7 класса).
Алгебраическая дробь – это алгебраическое выражение, числитель и знаменатель которого являются многочленами (при условии, что знаменатель не равен нулю).
Алгебраическая дробь, как и другие алгебраические выражения, может быть рациональной или иррациональной. Напомним, что в иррациональных выражениях извлекаются корня из переменных (или переменные возводятся в степень с дробным показателем). В рациональных выражениях корни и дробные степени или вообще не извлекаются или извлекаются только из чисел.
Алгебраические (рациональные) дроби
Алгебраическая дробь существует при условии, что её знаменатель не равен 0. Поэтому, если в знаменателе есть переменные («буквы»), всегда говорят о допустимых значениях этих переменных.
Основное свойство алгебраической дроби
При умножении или делении числителя и знаменателя алгебраической дроби на одно и то же алгебраическое выражение (отличное от нуля) получается равная ей дробь:
Это свойство аналогично основному свойству обычной числовой дроби: мы можем одновременно умножать или делить числитель и знаменатель на любое выражение, сокращать на общий множитель, если он существует. Например:
Приведение алгебраических дробей к общему знаменателю
Основное свойство алгебраических дробей позволяет приводить их к общему знаменателю и упрощать сложные выражения:
Алгоритм приведения алгебраических дробей к общему знаменателю
Шаг 2. Дополнительные множители
Перемена знака у члена дроби
Из основного свойства дроби следует, что одновременное умножение числителя и знаменателя на (-1) не изменит дробь:
Дробь также не изменится, если провести следующие перемены знаков:
Ещё несколько полезных формул, связанных с переменой знаков:
Примеры
Пример 1. Найдите допустимые значения переменных, входящих в дробь:
$ a^2-4 \neq 0 \iff (a-2)(a+2) \neq 0 \iff a \neq \pm 2$
$ 3x-1 \neq 0 \iff x \neq \frac<1><3>$
$$ x- \frac<4>
$ y^2-3|y| \neq 0 \iff |y|(|y|-3) \neq 0 \iff <\left\< \begin
Пример 2. Сократите дроби:
Пример 3. Упростите выражение:
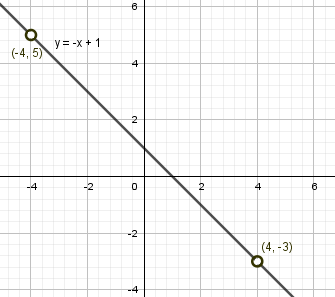
Пример 4. Постройте график функции:
(О графике линейной функции – см. §38 справочника для 7 класса)
Основное свойство алгебраических дробей
Определение алгебраической дроби
В §1 данного справочника мы уже давали определение алгебраических выражений, как целых, так и дробных. А в §14 данного справочника мы ввели понятие многочлена.
Алгебраическая дробь – это дробь, в которой числитель и знаменатель – многочлены (при условии, что знаменатель отличен от нуля).
Алгебраическая дробь существует при условии, что её знаменатель не равен 0. Поэтому, если в знаменателе есть переменные («буквы»), всегда говорят о допустимых значениях этих переменных.
При этом b может быть любым действительным числом, без ограничений.
Основное свойство алгебраической дроби
При умножении или делении числителя и знаменателя алгебраической дроби на одно и то же алгебраическое выражение (отличное от нуля) получается равная ей дробь:
Это свойство означает, что мы может сокращать алгебраическую дробь на общий множитель, если такой найдётся для числителя и знаменателя. Например:
Также, это свойство разрешает нам приводить алгебраические дроби к общему знаменателю и выполнять сложение или вычитание. Например:
Примеры
Пример 1. Найдите допустимые значения переменных, входящих в дробь:
Пример 2. Выразите переменные из формул:
а) s = vt. Найти v и t
б)m = ρV. Найти ρ и V
в) p = ρgh. Найти ρ и h
$$vt = x-x_0 \Rightarrow v = \frac
Пример 3. Сократите дроби:
Пример 4. Разложите на множители числитель и знаменатель и сократите дроби:
Основное свойство дроби: формулировка, доказательство, примеры применения
В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
a · m b · m = a b и a : m b : m = a b
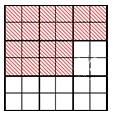
Разберем пример, который графически проиллюстрирует основное свойство дроби.
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4 · 9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4 · 5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:
Чтобы закрепить теорию, разберем решение примера.
Решение
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.
Что такое основное свойство алгебраической дроби
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
Несмотря на довольно большое внешнее отличие, существующее между алгебраическими и обыкновенными дробями, у них много общего, а именно: и обыкновенным, и алгебраическим дробям присущи одинаковое основное свойство и общие правила выполнения арифметических действий. В рамках этого урока мы столкнемся с понятиями: сокращение дроби, умножение и деление числителя и знаменателя на одно и то же выражение; также рассмотрим примеры.
Вспомним основное свойство обыкновенной дроби.
Значение обыкновенной дроби не изменится, если ее числитель и знаменатель умножить на одно и то же число, неравное нулю:
Также значение обыкновенной дроби не изменится, если числитель и знаменатель данной дроби разделить на одно и то же, отличное от нуля число (сократить):
Алгебраические дроби являются в некотором смысле обобщением обыкновенных дробей, и над ними можно проводить те же операции, что и над обыкновенными дробями.
Решим следующую задачу:
наименьшим общим кратным будет знаменатель 36c. Числитель и знаменатель дроби первой дроби необходимо умножить на 3, чтобы получить знаменатель 36c, а для второй дроби умножаем числитель и знаменатель на 2. Получаем:
Таким образом, воспользовавшись основным свойством алгебраической дроби, мы выполнили задание.
2) Чтобы привести данные дроби к общему знаменателю,
необходимо и знаменатель, и числитель второй дроби умножить на –1, получаем:
Не забываем, что m ≠ n. Таким образом, дроби:
имеют одинаковые знаменатели.
3) В данном случае просто умножим знаменатель и числитель первой дроби на знаменатель второй, и наоборот, знаменатель и числитель второй дроби – на знаменатель первой.
Это позволит нам привести дроби к одинаковому знаменателю.
В числителе раскрыли скобки, а в знаменателе воспользовались формулой разности квадратов.
Таким образом, с помощью дополнительных множителей (x – y) и (x + y) заданные дроби приведены к общему знаменателю:
Приводя алгебраические дроби к общему знаменателю, мы заменяли одну алгебраическую дробь другой дробью, тождественно равной первой.
Основное свойство алгебраической дроби: и числитель, и знаменатель алгебраической дроби можно умножить или разделить на один и тот же многочлен (в частности, одночлен или число, неравное нулю); это – тождественное преобразование заданной алгебраической дроби.
Тождественное преобразование алгебраической дроби путем деления её числителя и знаменателя на один и тот же многочлен (одночлен, число отличное от нуля) называют сокращением алгебраической дроби.
Например, алгебраическую дробь:
при необходимости можно заменить дробью:
числитель и знаменатель данной дроби умножили на x – y.
Пользуясь основным свойством алгебраической дроби, дробь:
можно сократить на a. Для этого необходимо предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общий множитель.