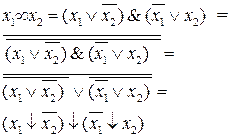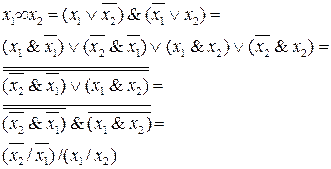Что такое основной базис алгебры логики определение
Основной базис алгебры логики



Очевидно, могут быть построены простейшие элементы, реализующие элементарные логические функции двух переменных f0 –f15. Сложные логические функции могут быть построены путем последовательного выполнения функциональных зависимостей, связывающих пары переменных.
Следовательно, имея элементы, осуществляющие элементарные операции f0 –f15, можно выполнить любую сложную логическую операцию. Такую систему функций можно назвать полной системой или базисом. Однако условие наличия 16 различных типов логических элементов, каждый из которых реализует одну из 16 элементарных функцій f0 –f15, является условием, достаточным для синтеза логического устройства любой сложности, но это условие не является необходимым, т. е. при синтезе можно ограничиться меньшим набором элементарных функций, взятых из f0 –f15.
Последовательно исключая из базиса функции, можно получить так называемый минимальный базис. Под минимальным базисом понимают такой набор функций, исключение из которого любой функции превращает этот набор в неполную систему функций.
Возможны различные базисы и минимальные базисы, различающиеся числом входящих в них функций и видом этих функций. Выбор того или иного базиса для синтеза логического устройства связан с тем, насколько просто, удобно и экономично технически выполнить элементы, реализующие элементарные функции, которые входят в выбранный базис, и в целом все логическое устройство.
Теперь можно сформулировать условие полноты системы функций алгебры логики.
Система функций будет полной (образует базис), если для любого из пяти рассмотренных свойств в этой системе найдется хотя бы одна функция, не обладающая этим свойством.
Таким образом, если бы полная система была составлена из функций, каждая из которых не обладала хотя бы одним из пяти свойств, то система включала бы в себя пять функций, а шестая была бы лишней. Однако некоторые функции не обладают несколькими свойствами. Так, например функции «ИЛИ-НЕ», «И-НЕ», не обладают ни одним из пяти свойств логических функций, поэтому они образуют минимальные базисы и на их основе можно построить логическое выражение любой сложности.
Логическое устройство, реализованное в базисах «ИЛИ-НЕ», «И-НЕ» имеет следующие преимущества:
-уменьшение номенклатуры элементов до одного типа упрощает компоновку устройства и его ремонт;
— наличие в каждом элементе инвертора (усилителя) компенсирует затухание потенциалов при передаче их через конъюнктор или дизъюнктор элемента, кроме того инвертор увеличивает нагрузочную способность элемента, а наличие емкости на выходе не вызывает длительного переходного процесса при смене потенциалов.
Именно поэтому элементы этих базисов широко выпускаются промышленностью в интегральном исполнении.
Рассмотрим представление логической функции «Эквивалентность» в базисах «ИЛИ-НЕ», «И-НЕ».
Чтобы выполнить преобразование, необходимо логическую функцию дважды проинвертировать и одну инверсию раскрыть по правилу Моргана, записывая логическое выражение через операцию «ИЛИ-НЕ» или «И-НЕ».
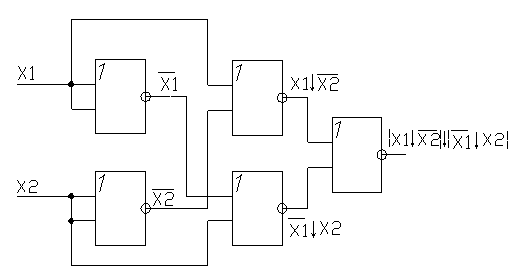
На рисунке 1.2.6.1. представлена схема, реализующая операцию «эквивалентность» в базисе «ИЛИ-НЕ».
Схема, реализующая операцию «эквивалентность» в базисе «ИЛИ-НЕ».
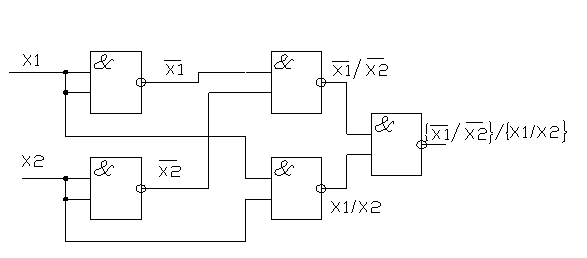
На рисунке 1.2.6.2. представлена схема, реализующая операцию «эквивалентность» в базисе «И-НЕ».
Схема, реализующая операцию «эквивалентность» в базисе «И-НЕ».
Булева алгебра (алгебра логики)
Понятие алгебры логики
На этом уроке знакомимся с алгеброй логики (булевой алгеброй). Одним из её основателей стал английский математик Джордж Буль (1815-1864), который был из довольно бедной семьи, а в юности зарабатывал переводами сочинений древнегреческих философов. За этим занятием его и посетила мысль о том, что высказываниям можно присваивать значения 1 («истина») и 0 «ложь».
Итак, алгебра логики (булева алгебра) — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики позволяет закодировать любые утверждения, истинность или ложность которых нужно доказать, а затем манипулировать ими подобно обычным числам в математике.
Создание алгебры логики в середине ХIХ века в трудах Джорджа Буля представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Пусть функция 

Значениям переменной в булевой алгебре соответствуют состояниям элементов микросхем компьютера или любого другого электронного устройства: сигнал присутствует (логическая «1») или сигнал отсутствует (логический «0»).
На логических элементах, реализующих булевы функции, строятся логические схемы электронных устройств.
Часто оказывается, что изначально построенное логическое выражение можно упростить, используя аксиомы, теоремы и законы алгебры логики.
Логические функции
Логические функции одной переменной
| Функция | Название | Обозначение |
 | Константа нуля |  |
 | Повторение x |  |
 | Логическое отрицание, инверсия, «НЕ» |  |
 | Константа единицы |  |
| Переменная | Логические функции | |||
| x |  |  |  |  |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Логические функции двух переменных
| Функция | Название | Обозначение |
 | Константа нуля |  или False или False |
 | Логическое умножение, конъюнкция, «И» |  или или  или или  или или  |
 | Запрет по  |  или или  |
 | Переменная  |  |
 | Запрет по  |  или или  |
 | Переменная  |  |
 | Сложение по модулю 2, отрицание эквивалентности, исключающее «ИЛИ» |  или или  или или  |
 | Логическое сложение, дизъюнкция, «ИЛИ» |  или или  или или  или или  |
 | Функция Пирса (Вебба), «ИЛИ-НЕ» |  или или  или или  |
 | Логическая равнозначность, эквиваленция |  или или  или или  или или  |
 | Отрицание  |  |
 | Правая импликация |  или или  |
 | Отрицание  |  |
 | Левая импликация |  или или  |
 | Функция Шеффера, «И-НЕ» |  или или  или или  |
 | Константа единицы |  или True или True |
Ниже дана таблица истинности для логических функций от двух переменных.
| X1 | 0 | 0 | 1 | 1 |
| X2 | 0 | 1 | 0 | 1 |
 | 0 | 0 | 0 | 0 |
 | 0 | 0 | 0 | 1 |
 | 0 | 0 | 1 | 0 |
 | 0 | 0 | 1 | 1 |
 | 0 | 1 | 0 | 0 |
 | 0 | 1 | 0 | 1 |
 | 0 | 1 | 1 | 0 |
 | 0 | 1 | 1 | 1 |
 | 1 | 0 | 0 | 0 |
 | 1 | 0 | 0 | 1 |
 | 1 | 0 | 1 | 0 |
 | 1 | 0 | 1 | 1 |
 | 1 | 1 | 0 | 0 |
 | 1 | 1 | 0 | 1 |
 | 1 | 1 | 1 | 0 |
 | 1 | 1 | 1 | 1 |
Ответить на контрольные вопросы, а затем посмотреть ответы
Контрольный вопрос 2. Какие из функций не являются ФАЛ одной переменной (и одна, и вторая в варианте ответа):
Булев базис (логический базис)
Любую булеву функцию с произвольным количеством аргументов можно построить через подстановку элементарных функции вместо аргументов (суперпозицию). Набор простейших функций, с помощью которого можно выразить любые другие, сколь угодно сложные логические функции, называется функционально полным набором, или логическим базисом.
Инверсия (логическое отрицание, «НЕ»)

 |  |
| 0 | 1 |
| 1 | 0 |
Конъюнкция (логическое умножение, «И»)

 |  |  |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Дизъюнкция (логическое сложение, «ИЛИ»)

 |  |  |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Аналитическое представление логических функций
Дизъюнктивная нормальная форма

| X1 | X2 | f |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Конъюнктивная нормальная форма

| X1 | X2 | f |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Способы описания логических функций
Применяются следующие способы описания логических функций:
| Номер набора | f |
| 0 | 0 |
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 1 |
| 6 | 0 |
| 7 | 1 |
| X1 | X2 | X3 | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Пример числового описания логических функций


Пример аналитического описания логических функций
Пример координатного описания логических функций
Пример графического описания логических функций
Аксиомы алгебры логики
Аксиомы конъюнкции

Аксиомы дизъюнкции

Аксиомы отрицания
если 



Теоремы алгебры логики
Теоремы исключения констант

Теоремы идемпотентности (тавтологии, повторения)


Теорема противоречия

Теорема «исключённого третьего»

Теорема двойного отрицания (инволюции)

Законы алгебры логики
Ассоциативный (сочетательный) закон

Коммутативный (переместительный) закон

Дистибутивный (распределительный) закон


Законы де Моргана (законы общей инверсии или дуальности)


Закон поглощения (элиминации)

Закон склеивания (исключения)