Что такое особая точка функции

Что такое особая точка функции

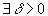
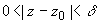
Точка z₀, принадлежащая области комплексных чисел, называется изолированной особой точкой функции f(z), если такая, что f(z) является однозначной аналитической функцией в (в самой точке аналитичность f(z) нарушается).

ПРИМЕР 1. Отыскание особых точек рациональной дроби.

ПРИМЕР 2. Определение типа особых точек.

ПРИМЕР 3. Определение типа особой точки.

Для того чтобы особая точка функции была полюсом, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала конечное число членов.

Ряд Лорана функции f(z) в случае z₀-полюс имеет вид:
(2)
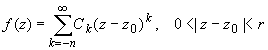
если z₀ принадлежит области комплексных чисел.

Номер старшего члена главной части ряда Лорана функции в ее разложении в окрестности полюса называется порядком полюса.
Так, точка z₀ является полюсом порядка n функции f(z), если в разложении (2) 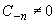, C_k = 0 при k

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Особая точка функции

Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например, точка в которой функция недифференцируема).

Особенности в комплексном анализе

Комплексный анализ рассматривает особенности голоморфных (более общо: аналитических) функций — точки комплексной плоскости, в которой эта функция не определена, её предел бесконечен либо предела не существует вовсе. В случае точек ветвления аналитических функций функция в особой точке может быть определена и непрерывна, но не являться аналитичной.

Особенности в действительном анализе

Полезное

Смотреть что такое «Особая точка функции» в других словарях:

ОСОБАЯ ТОЧКА — аналитической функции точка, в которой нарушается аналитичность функции … Большой Энциклопедический словарь

ОСОБАЯ ТОЧКА — аналитической функции точка, в к рой нарушаются условия аналитичности. Если аналитическаяфункция f(z )задана в нек рой окрестности точки z0 всюду … Физическая энциклопедия

Особая точка — в математике. 1) Особая точка кривой, заданной уравнением F (x, у) = 0, точка М0(х0, y0), в которой обе частные производные функции F (x, у) обращаются в нуль: Если при этом не все вторые частные производные… … Большая советская энциклопедия

ОСОБАЯ ТОЧКА — 1) О. т. аналитической функции f(z) препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого либо пути на плоскости этого переменного. Пусть аналитическая функция f(z) определена некоторым… … Математическая энциклопедия

особая точка — аналитической функции, точка, в которой нарушается аналитичность функции. * * * ОСОБАЯ ТОЧКА ОСОБАЯ ТОЧКА аналитической функции, точка, в которой нарушается аналитичность функции … Энциклопедический словарь

ПОДВИЖНАЯ ОСОБАЯ ТОЧКА — особая точка z0 решения дифференциального уравнения F(z, w, w )=0 (F аналитич. функция), рассматриваемого как функция w(z).комплексного переменного z, при условии, что решения того же уравнения с близкими начальными данными имеют близкие к z0… … Математическая энциклопедия

СУЩЕСТВЕННО ОСОБАЯ ТОЧКА — изолированная особая точка а однозначного характера аналитич. ции f(z) комплексного переменного z, для к рой не существует никакого, конечного или бесконечного, предела В достаточно малой проколотой окрестности С. о. т. или в случае функция… … Математическая энциклопедия

Существенно особая точка — аналитической функции, точка z0 комплексной плоскости, в которой не существует ни конечного, ни бесконечного предела при z → z0 для функции, однозначной и аналитической в некоторой окрестности этой точки (см. Аналитические функции).… … Большая советская энциклопедия

Источник

Что такое особая точка функции

ОСОБЫЕ ТОЧКИ И ИХ КЛАССИФИКАЦИЯ

Точка аС z называется изолированной особой точкой однозначного характера функции f ( z ), если f ( z ) аналитическая и однозначная (регулярная) в кольце < z :0 z – a | r >, а в самой точке а не определена.

Бесконечно удаленная точка называется изолированной особой точкой однозначного характера функции f ( z ), если f ( z ) регулярна в некоторой окрестности < R z | z= и функция

имеет в точке x = 0 изолированную особую точку однозначного характера.

В зависимости от поведения функции f ( z ) вблизи точки а различают следующие три типа особых точек.

Изолированная особая точка а функции f ( z ) называется

а) устранимой особой точкой, если существует конечный предел

в) существенно особой точкой, если

Заметим, что типы особых точек z = функции f ( z ) и x = 0 функции j(x) совпадают, ибо

f ( a )= f ¢ ( a )=…= f ( m-1 ) ( a ) =0,

f (m) ( a ) 0.

При т =1 точка а называется простым нулем функции f ( z ), при m >1-кратным.

Порядком (или кратностью) полюса функции g ( z ) в точке а называется кратность нуля в точке а регулярной функции

, где P ( z ) и Q ( z ) – полиномы, не имеющие общих корней, то корни полинома Q ( z ) (и только они) являются полюсами функции f ( z ).

Порядок полюса f ( z ) совпадает с кратностью соответствующих корней полинома Q ( z ).

Точка z= называется нулем кратности m 1 для функции f ( z ), регулярной в этой точке, если функция

имеет нуль кратности т в точке x =0.

Если z=а – изолированная особая точка однозначного характера для функции f ( z ), то f ( z ) регулярна в некотором кольце < z : 0 z-a | r >и ее можно разложить в ряд Лорана, сходящийся в этом кольце,

.

Тип изолированной особой точки однозначного характера определяется видом лорановского разложения функции в проколотой окрестности этой точки.

2. Для того чтобы точка а была полюсом функции f ( z ), необходимо и достаточно, чтобы главная часть лорановского разложения функции f ( z ) в окрестности этой точки содержала лишь конечное число членов (причем полюсом порядка т ³ 1, если главная часть имеет вид

, где с т 0.

3. Точка а тогда и только тогда является существенно особой, когда главная часть лорановского разложения функции f ( z ) в окрестности этой точки содержит бесконечно много отличных от нуля членов.

Разложение функции f ( z ) в окрестности бесконечно удаленной точки в ряд Лорана имеет вид

Опираясь на приведенные критерии типа особой точки и определение вычета в точке z = , рекомендуем читателю сформулировать соответствующие утверждения для точки z = .

Источник

Особая точка

Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например, точка в которой функция недифференцируема).

Особенности в комплексном анализе

Комплексный анализ рассматривает особенности голоморфных (более общо: аналитических) функций — точки комплексной плоскости, в которой эта функция не определена, её предел бесконечен либо предела не существует вовсе. В случае точек ветвления аналитических функций функция в особой точке может быть определена и непрерывна, но не являться аналитичной.

Особенности в действительном анализе

Полезное

Смотреть что такое «Особая точка» в других словарях:

ОСОБАЯ ТОЧКА — аналитической функции точка, в к рой нарушаются условия аналитичности. Если аналитическаяфункция f(z )задана в нек рой окрестности точки z0 всюду … Физическая энциклопедия

ОСОБАЯ ТОЧКА — аналитической функции точка, в которой нарушается аналитичность функции … Большой Энциклопедический словарь

особая точка — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN singular point … Справочник технического переводчика

Особая точка — в математике. 1) Особая точка кривой, заданной уравнением F (x, у) = 0, точка М0(х0, y0), в которой обе частные производные функции F (x, у) обращаются в нуль: Если при этом не все вторые частные производные… … Большая советская энциклопедия

ОСОБАЯ ТОЧКА — 1) О. т. аналитической функции f(z) препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого либо пути на плоскости этого переменного. Пусть аналитическая функция f(z) определена некоторым… … Математическая энциклопедия

особая точка — аналитической функции, точка, в которой нарушается аналитичность функции. * * * ОСОБАЯ ТОЧКА ОСОБАЯ ТОЧКА аналитической функции, точка, в которой нарушается аналитичность функции … Энциклопедический словарь

особая точка — ypatingasis taškas statusas T sritis automatika atitikmenys: angl. singular point vok. singulärer Punkt, m rus. особая точка, f pranc. point particulier, m; point singulier, m … Automatikos terminų žodynas

особая точка — ypatingasis taškas statusas T sritis fizika atitikmenys: angl. singular point vok. singulärer Punkt, m rus. особая точка, f pranc. point singulier, m … Fizikos terminų žodynas

Особая точка функции — Особая точка указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например,… … Википедия

Особая точка дифференциального уравнения — У термина «особая точка» существуют и другие значения. В математике, особой точкой векторного поля называется точка, в которой векторное поле равно нулю. Траектория соответствующего автономного обыкновенного дифференциального уравнения,… … Википедия

Источник

ОСОБАЯ ТОЧКА

аналитической функции- точка, в к-рой нарушаются условия аналитичности. Если аналитическаяфункция f(z )задана в нек-рой окрестности точки z₀ всюду,

Полезное

Смотреть что такое «ОСОБАЯ ТОЧКА» в других словарях:

Особая точка — указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например, точка в которой… … Википедия

ОСОБАЯ ТОЧКА — аналитической функции точка, в которой нарушается аналитичность функции … Большой Энциклопедический словарь

особая точка — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN singular point … Справочник технического переводчика

Особая точка — в математике. 1) Особая точка кривой, заданной уравнением F (x, у) = 0, точка М0(х0, y0), в которой обе частные производные функции F (x, у) обращаются в нуль: Если при этом не все вторые частные производные… … Большая советская энциклопедия

ОСОБАЯ ТОЧКА — 1) О. т. аналитической функции f(z) препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого либо пути на плоскости этого переменного. Пусть аналитическая функция f(z) определена некоторым… … Математическая энциклопедия

особая точка — аналитической функции, точка, в которой нарушается аналитичность функции. * * * ОСОБАЯ ТОЧКА ОСОБАЯ ТОЧКА аналитической функции, точка, в которой нарушается аналитичность функции … Энциклопедический словарь

особая точка — ypatingasis taškas statusas T sritis automatika atitikmenys: angl. singular point vok. singulärer Punkt, m rus. особая точка, f pranc. point particulier, m; point singulier, m … Automatikos terminų žodynas

особая точка — ypatingasis taškas statusas T sritis fizika atitikmenys: angl. singular point vok. singulärer Punkt, m rus. особая точка, f pranc. point singulier, m … Fizikos terminų žodynas

Особая точка функции — Особая точка указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например,… … Википедия

Особая точка дифференциального уравнения — У термина «особая точка» существуют и другие значения. В математике, особой точкой векторного поля называется точка, в которой векторное поле равно нулю. Траектория соответствующего автономного обыкновенного дифференциального уравнения,… … Википедия

Источник