Что такое открытая дуга на числовой окружности

1. Конспект для учителя по теме «Числовая окружность»

Что такое числовая окружность? Для чего она нужна?

Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Сегодня мы будем учиться использовать единичную окружность.

Для успешной работы с единичной окружностью нужно знать всего три вещи.

Первое. Надо знать, что такое синус, косинус, тангенс и котангенс в применении к прямоугольному треугольнику.

Второе. Надо знать, что такое тригонометрический круг, единичная окружность, числовая окружность.

Третье. Надо знать, как отсчитывать углы на тригонометрическом круге, и что такое градусная и радианная меры углов.

Угол поворота – это угол, полученный вращением луча около его начала О от начального положения ОА до конечного положения ОВ.

Угол в 1— это центральный угол, опирающийся на дугу, длина которой равна части окружности.

В зависимости от того в какой координатной четверти окажется начальный радиус, угол α называют углом этой четверти:

Источник

2. Конспект для ученика по теме «Числовая окружность»

Что такое числовая окружность? Для чего она нужна? И как она связана с тригонометрией?

Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Сегодня мы будем учиться использовать единичную окружность.

Для успешной работы с единичной окружностью нужно знать всего три вещи.

Первое. Надо знать, что такое синус, косинус, тангенс и котангенс в применении к прямоугольному треугольнику.

Второе. Надо знать, что такое тригонометрический круг, единичная окружность, числовая окружность.

Третье. Надо знать, как отсчитывать углы на тригонометрическом круге, и что такое градусная и радианная меры углов.

Угол поворота – это угол, полученный вращением луча около его начала О от начального положения ОА до конечного положения ОВ.

Угол в 1— это центральный угол, опирающийся на дугу, длина которой равна части окружности.

В зависимости от того в какой координатной четверти окажется начальный радиус, угол α называют углом этой четверти:

Источник

Числовая окружность

1) Начало отсчета находится в крайней правой точке окружности;

3) Если в положительном направлении отложить на окружности расстояние \(t\), то мы попадем в точку со значением \(t\);

4) Если в отрицательном направлении отложить на окружности расстояние \(t\), то мы попадем в точку со значением \(–t\).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.

Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен \(1\). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках \(1\) и \(-1\).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).

Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы \(l=2πR\) мы получим:

Длина числовой окружности равна \(2π\) или примерно \(6,28\).

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте \(1\) на оси \(x\) и \(0\) на окружности – это точки на разных объектах.

Какие точки соответствуют числам \(1\), \(2\) и т.д?

Помните, мы приняли, что у числовой окружности радиус равен \(1\)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.

Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу \(2\), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы \(3\) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: \(2π\). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа \(π\) : \( \frac<π><2>\),\(-\frac<π><2>\),\(\frac<3π><2>\), \(2π\). Поэтому при работе с окружностью чаще используют числа с \(π\). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).

Главное свойство числовой окружности

Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.

И следствие из этого правила:

Все значения одной точки на числовой окружности можно записать с помощью формулы:

Что надо запомнить про числовую окружность:

Источник

Урок-лекция «Числовая окружность»

Подготовка. На стенде в кабинете математики оформить сообщение об истории возникновении тригонометрии.
Приложение.

1. Организационный момент.

Сообщить учащимся тему урока и ее место в изучении блока “Тригонометрия”, сообщить план изучения материала (план лекции). (Слайд 1, 2)

Далее материал урока изучается с помощью презентации.

2. Актуализация знаний.

Повторить понятие числовой прямой (задание числовой прямой, расположение точек на числовой прямой, соответствие точек и чисел на числовой прямой). (Слайд 3)

3. Изучение нового материала.

Обратить внимание учащихся на коэффициенты чисел вида на первом макете (начиная с первой точки – коэффициенты: 1,3,5,7… – т.е. числа нечетные).

Показать движение на втором макете: маленькие шаги , большие шаги , два маленьких шага по – это один большой .

Отрабатывать умение строить “макетные” точки и определять числа которым соответствуют заданные точки, обращая внимание на то, что чисел много. (Слайд 8, 9)

4. Напомнить учащимся, как на числовой прямой аналитически записывали множество точек промежутка. Обратить внимание на направление движения: слева направо, т.е. в положительном направлении и на характер точек на концах промежутка.

Показать примеры (Слайд 10) аналитических записей открытых дуг числовой окружности по алгоритму:

– определить точку начала и точку конца дуги;

– зафиксировать направление движения (против часовой стрелки);

– записать все числа, соответствующие началу дуги, затем все числа, соответствующие концу дуги;

– записать соответствующее двойное неравенство (дуга открытая!)

Отрабатывать умение записывать аналитически заданные открытые дуги. (Слайд 11)

4. Подведение итогов урока.

Фронтальный опрос с опорой на план лекции (Слайд 12):

В чем отличие и в чем сходство расположения и построения точек на числовой прямой и числовой окружности?

В каком направлении надо двигаться от начала отсчета, чтобы отметить положительные и отрицательные точки на числовой прямой (окружности)?

Как записать аналитическую запись открытой, закрытой дуги?

5. Домашнее задание.

Задание дается по учебнику А.Г.Мордковича “Алгебра и начала анализа”, 2009 г. (базовый уровень). (Слайд13)

Источник

Что такое открытая дуга на числовой окружности

Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.

Единичной окружностью называют окружность радиуса 1.

Общий вид числовой окружности.

1) Ее радиус принимается за единицу измерения.

2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.

3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:

первая четверть – это дуга AB

вторая четверть – дуга BC

третья четверть – дуга CD

четвертая четверть – дуга DA

4) Начальная точка числовой окружности – точка А.

Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.

Числовая окружность на координатной плоскости.

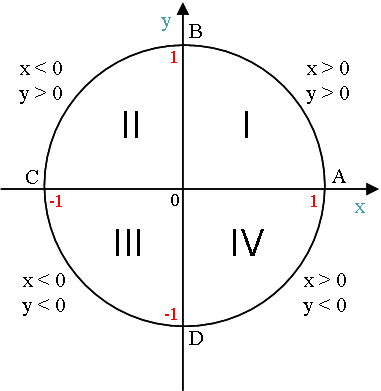
Центр радиуса числовой окружности соответствует началу координат (числу 0).

Горизонтальный диаметр соответствует оси x, вертикальный – оси y.

Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).

Значения x и y в четвертях числовой окружности:

x 0, y Основные величины числовой окружности:

Величина
в радианах

Величина
в радиусах

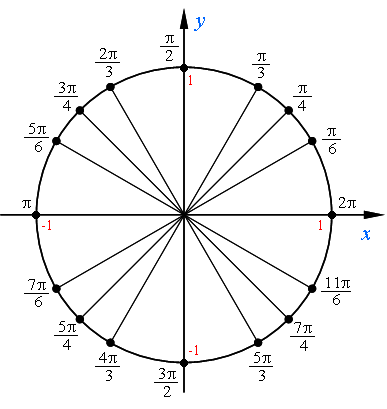
Имена и местонахождение основных точек числовой окружности:

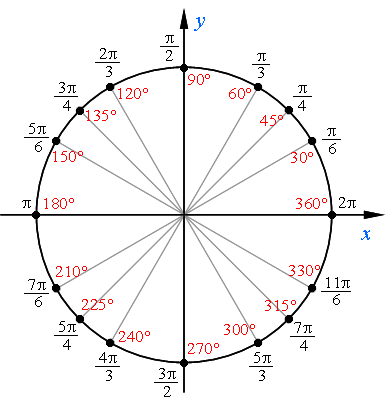
Как запомнить имена числовой окружности.

Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.

Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.

1) Начнем с крайних точек на осях координат.

Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).

Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.

2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.

Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:

— Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.

— Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.

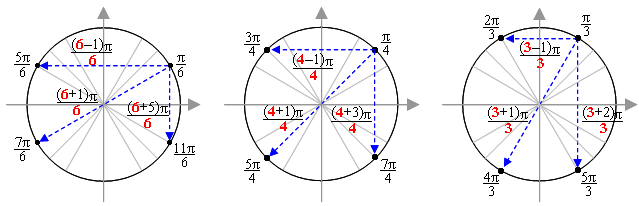
Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.

— Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.

Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.

3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.

Особенности числовой окружности. Сравнение с числовой прямой.

Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.

На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:

Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.

Отсюда формула:

Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число:

M(t) = M(t + 2πk),

где k ∈ Z.

Число k называется параметром.

Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):

Источник