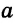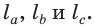Что такое отложить отрезок

Задачи на построение по геометрии с примерами решения

Содержание:

Ранее мы выполняли построения на плоскости при помощи линейки с делениями, чертежного треугольника, транспортира и циркуля.

Математиков всегда интересовали построения геометрических фигур, которые можно выполнить только при помощи циркуля и линейки. В геометрии специально выделяют задачи на построение, которые могут быть решены с помощью этих двух инструментов.

Например, при помощи циркуля и линейки можно построить треугольник, стороны которого равны трем данным отрезкам. Или построить угол, равный данному углу.

Рассмотрим одну из таких задач на построение. На прямой

Найти точку — это значит построить ее при помощи циркуля и линейки. Если перемещать некоторую точку по прямой (положения К₁ К₂, К₃), то расстояния от этой точки до точек А и В будут меняться. Когда эти расстояния станут равными, точка на прямой будет равноудалена от концов отрезка АВ. Значит, она будет лежать на серединном перпендикуляре к отрезку АВ. Это и есть идея построения: нужно построить серединный перпендикуляр к отрезку АВ и найти точку его пересечения с прямой .

Чтобы построить серединный перпендикуляр, нужно построить две пересекающиеся окружности равных радиусов с центрами в точках А к В (рис. 293, б). Затем провести прямую MN через точки пересечения этих окружностей (ниже мы обоснуем это построение). В пересечении серединного перпендикуляра MN к отрезку АВ и прямой 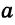получим искомую точку К.

Рассмотренная задача может иметь и практический смысл. Допустим, есть два населенных пункта и шоссе рядом с ними. На шоссе нужно найти место для остановки, чтобы путь для жителей обоих населенных пунктов до остановки был одинаковым. Все построения будут сделаны на карте населенного пункта.

При решении задач на построение линейка считается односторонней и без делений. При помощи такой линейки нельзя построить две параллельные прямые, проведя линии по краям линейки, нельзя измерять и откладывать отрезки, нельзя строить перпендикуляры, используя прямоугольную форму линейки. Рассмотрим, какие операции можно выполнять линейкой, а какие циркулем.

Операции с линейкой

При помощи линейки можно провести (построить):

а) произвольную прямую;

б) прямую, проходящую через две точки (рис. 294).

Операции с циркулем

При помощи циркуля можно:

а) построить произвольную окружность и окружность (дугу окружности) с данным центром и радиусом, равным данному отрезку (рис. 295);

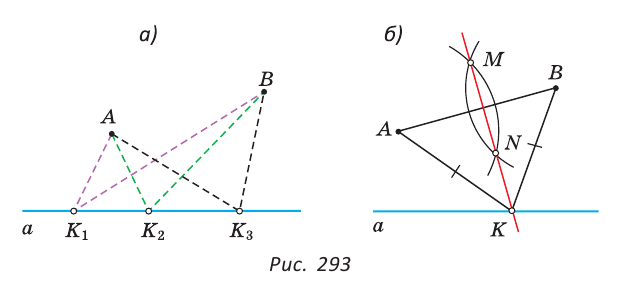
б) отложить отрезок, равный данному отрезку, на некоторой прямой.

Откладывание отрезка

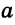
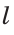
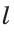
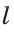
Для откладывания отрезка, равного данному отрезку (рис. 296, а) на прямой (рис. 296, б), следует: 1) отметить на прямой точку М; 2) радиусом, равным а, провести дугу окружности с центром в точке М (сделать засечку на прямой ).

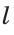
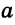
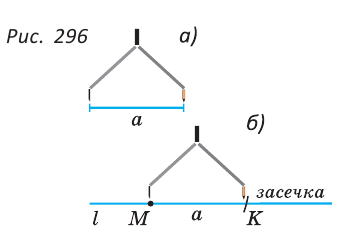
В пересечении дуги и прямой получим точку К и отрезок МК, равный .

Операция откладывания отрезка на прямой позволяет построить сумму и разность двух отрезков (рис. 297): в первом случае на произвольной прямой откладывают последовательно два отрезка, во втором — на большем отрезке от любого его конца откладывают меньший отрезок.

В дальнейшем при решении задач на построение мы не будем описывать процедуру откладывания отрезка на прямой, считая ее элементарной операцией.

Перечислим 5 основных задач на построение, к которым сводятся другие задачи. Решая сложные задачи, будем ссылаться на эти основные, не описывая ту часть решения, которая связана с одной из основных задач.

В некотором смысле «линейка» и «циркуль» — это два идеальных робота, которые могут выполнять определенный набор операций. И наша задача — составить алгоритм из последовательности таких операций — команд для этих роботов, который приведет к построению необходимой фигуры. Фактически нужно написать программу для «циркуля» и «линейки».

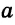
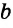
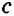
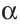
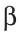
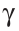
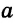
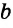
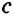
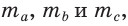
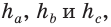
Замечание. В треугольнике ABC стороны, противолежащие углам А, В и С, будем соответственно обозначать , и , а сами эти углы — , и (рис. 298). Медианы, проведенные к сторонам , и , — высоты — биссектрисы —

Построение треугольника по трем сторонам. Построение угла, равного данному

Задача №1

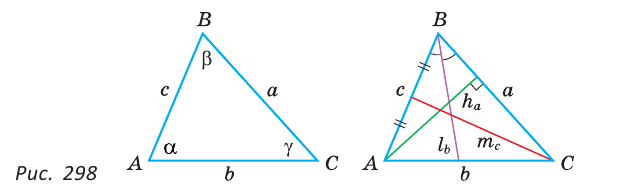
Построить треугольник со сторонами , и .

Решение:

Пусть даны отрезки , и . На произвольной прямой откладываем отрезок АВ = (рис.300).

Строим окружность с центром в точке А радиусом . Строим окружность с центром в точке В радиусом . Находим точку С пересечения этих окружностей. Проведем отрезки АС и ВС.

Треугольник ABC — искомый, так как у него ВС = , АС = , АВ = по построению.

Задача имеет решение, если для данных отрезков , и выполняется неравенство треугольника:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Отрезок. Ломаная линия

Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.

Рис. 1 Отрезок на прямой

Рис. 2 Несколько отрезков на прямой

Отрезок делит прямую линию на три объекта (смотри рисунок 3):

То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.

Рис. 3 Отрезок и лучи прямой

Рис. 4 Отрезок без прямой

Рис. 5 Отрезок и принадлежащие ему точки

Так, на рисунке 5 видно, что:

В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.

Рис. 6 Отрезок и части отрезка

Построение и измерение отрезка

Произвольный отрезок можно построить двумя способами:

Рис. 7 Построение произвольного отрезка

Измерить отрезок можно:

Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).

Рис. 8 Сравнение отрезков

На рисунке 8 видно, что:

Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.

Длина отрезка – это расстояние между концами этого отрезка.

Равные отрезки — это такие отрезки, которые имеют одинаковую длину.

На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?

Рис. 9 Измерение длины отрезка

Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.

Рис. 10 Построение отрезка заданной длины

Отрезок — это самое короткое расстояние между двумя точками.

В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.

Рис. 11 Кривая, ломаная, отрезок

Ломаная линия

Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.

Рис. 12 Ломаная линия

На рисунке 12 видно, что:

Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.

Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.

Рис. 12. Замкнутая и разомкнутая ломаные линии

Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.

Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.

Рис. 13. Самопересекающиеся ломаные линии

Источник

Отрезок

Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.

Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.

Длина отрезка

Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:

Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:

длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.

Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:

Свойства длин отрезков:

Равные отрезки

Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.

Пример. Возьмём два отрезка CD и LM:

Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:

Значит длины отрезков равны, следовательно CD = LM.

Сравнение отрезков

Сравнить два отрезка — это значит определить, равны они, или один больше другого.

Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.

Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.

При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.

Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):

Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):

CA > CB или CB Пример. Сравнить длину отрезков AB и AC.

Так как отрезок AB имеет большую длину, чем отрезок AC, то

Так как отрезки AB и AC имеют одинаковую длину, то

Если при измерении отрезков их длины равны, то и отрезки равны.

Середина отрезка

Середина отрезка — это точка, делящая отрезок на две равные части.

Источник

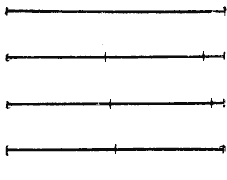
Сравнение отрезков. Действия над отрезками.

Равные и неравные отрезки

Пусть нам даны два отрезка АВ и СD (рис.). Наложим отрезок АВ на отрезок CD так, чтобы точка А совпала с точкой С, и отрезок АВ направим по отрезку CD. Если точка В совпадаете точкой D, то отрезки АВ и CD равны; АВ = CD.

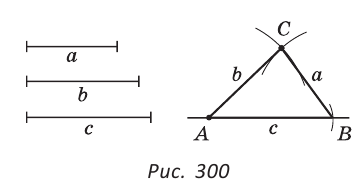
Сравним два отрезка КО и ЕМ (рис.).

Наложим отрезок КО на отрезок ЕМ так, чтобы точки К и Е совпали. Отрезок КО направим по отрезку ЕМ. Если точка О окажется где-нибудь между точками Е и М, то говорят, что отрезок ЕМ больше отрезка КО; отрезок КО меньше отрезка ЕМ.

Записывается это тaк: ЕМ > КО, КО 1 /₅ часть отрезка МN.

в) Чтобы разделить отрезок на равные части с помощью циркуля, поступают таким образом. Например, если нужно разделить отрезок на две равные части, то циркуль раздвигают на глаз так, чтобы раствор циркуля составлял примерно половину отрезка. Затем на данном отрезке от его конца последовательно один за другим откладывают этим раствором циркуля два отрезка. Если полученная сумма отрезков будет меньше данного отрезка, тo раствор циркуля увеличивают; если сумма окажется больше данного отрезка, то раствор циркуля уменьшают. Так, постепенно исправляя ошибку, можно отыскать довольно точнo половину отрезка (рис.).

Свойство отрезков, отсекаемых параллельными прямыми на сторонах угла

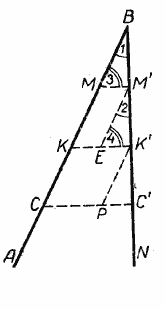
Пусть на стороне АВ угла АВN отложены равные отрезки ВМ = МК = КС (рис.) и через точки деления М, К и С проведены параллельные прямые, пересекающие сторону ВN того же угла.

На этой стороне образовались три отрезка: ВМ’, М’К’ и К’С’. Требуется доказать, что ВМ’ = М’К’ = К’С’.

Для доказательства через точки М’ и К’ проведём прямые, параллельные АВ. Мы получим треугольники ВММ’, М’ЕК’ и К’РС’. Сравним эти треугольники.

Сначала сравним треугольники МВМ’ и М’ЕК’. В этих треугольниках имеем:

∠1 = ∠2, как соответственные углы при параллельных ВА и М’Е и секущей ВN;

∠3 = ∠4, как острые углы 1 с соответственно параллельными сторонами (АВ || М’Е и ММ’ || КК’).

ВМ = МК по построению;

МК = М’Е, как противоположные стороны параллелограмма.

Углы 1-й и 4-й могут оказаться оба тупыми, но и в этом случае они останутся равными, а потому доказательство теоремы не изменится.

Следовательно, ВМ = М’Е. Таким образом, ΔВММ’ = ΔМ’ЕК’ (по стороне и двум прилежащим к ней углам). Отсюда следует, что ВМ’ = М’К’.

Так же можно доказать, что ВМ’ = К’С’, т. е. ВМ’ = М’К’ = К’С’. При доказательстве теоремы мы откладывание отрезков начали от вершины угла, но теорема справедлива и для того случая, когда откладывание отрезков будет начато не от вершины угла, а от любой точки его стороны.

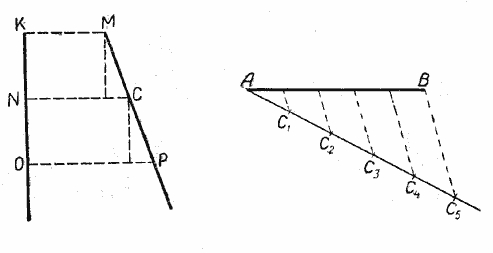
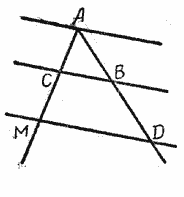
В этом случае вершину угла на чертеже можно не отмечать (рис.).

Теорема справедлива и для случая, когда прямые КО и МР параллельны.

Пропорциональные отрезки

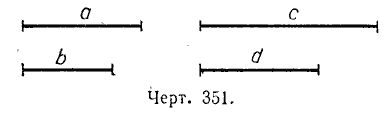
Из арифметики известно, что равенство двух отношений называется пропорцией. Например: 16 /₄ = 20 /₅; 2 /₃ = 4 /₆ To же самое имеем и в геометрии: если даны две пары отрезков, отношения которых равны, то можно составить пропорцию.

отрезки а, b, c, d называются пропорциональными.

В пропорции можно поменять местами отношения; можно переставить крайние члены, средние члены; можно переставить те и другие одновременно.

Поскольку в пропорции a /_b = c /_d под буквами подразумевают числа, выражающие длины отрезков, то произведение крайних членов её равно произведению средних членов. Отсюда, зная три члена пропорции, можно найти неизвестный четвёртый её член. Так, в пропорции a /_x = c /_d x = a • d /_c

Отметим ещё некоторые свойства пропорций, которыми придётся в дальнейшем пользоваться при доказательстве некоторых теорем и при решении задач.

а) Если три члена одной пропорции соответственно равны трём членам другой пропорции, то равны и четвёртые члены этих пропорций.

Чтобы убедиться в этом, переставим средние члены в этой пропорции.

А это возможно лишь в том случае, когда числитель и знаменатель дроби равны, т. е.

В справедливости этого свойства предлагается вам убедиться самостоятельно. Для этого проведите рассуждение, аналогичное предыдущему.

Построение пропорциональных отрезков

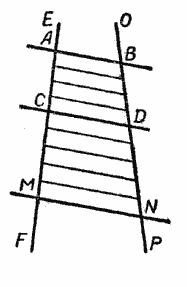
Пусть две прямые ЕF и ОР пересечены тремя параллельными прямыми АВ, СD и МN (рис.).

Требуется доказать, что отрезки АС, СМ, ВD и DN, заключённые между параллельными секущими, пропорциональны, т. е.

Пусть длина отрезка АС равна р, а длина отрезка СМ равна q.

Например, р = 4 см. и q = 5 см.

Разделим АС и СМ на отрезки, равные 1 см, и из точек деления проведём прямые, параллельные прямым АВ, СD и МN, как это показано на рисунке.

Тогда на прямой ОР отложатся равные между собой отрезки, при этом на отрезке BD их будет 4, а на отрезке DN — 5.

Значит, отрезки АС, СМ, ВD и DN пропорциональны. Пропорциональны также и отрезки АС, АМ, ВD и ВN (налегающие друг на друга), т. е. AC /_AM = BD /_BN,

Теорема будет справедлива и при любых других целых значениях р и q.

Если длины отрезков АС и СМ не выразятся в целых числах при данной единице измерения (например, сантиметре), то надо взять такую более мелкую единицу (например, миллиметр или микрон), при которой длины отрезков АС и СМ практически выразятся в целых числах.

Доказанная теорема справедлива и в том случае, когда одна из параллельных секущих проходит через точку пересечения данных прямых. Она справедлива также и в том случае, когда отрезки откладываются не непосредственно один за другим, а через некоторый промежуток.

Источник