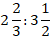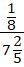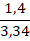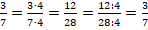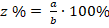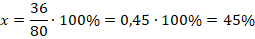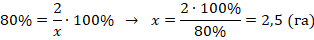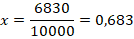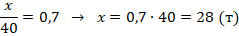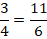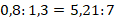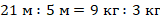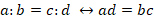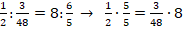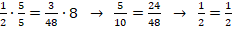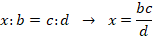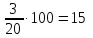Что такое отношение чисел 6 класс
Урок 21 Бесплатно Отношения
В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.
Отношение
Начнем с определения:
Отношением двух чисел называют частное этих двух чисел.
Записать отношение числа a к числу b мы можем как \(\mathbf\) или же через дробную черту: \(\mathbf<\frac>\)
У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:
Посмотрим на разные примеры.
Пример 1
Найдем отношение чисел 256 и 8
По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.
Ответом будет 32.
Иными словами, 256 относится к 8 как 32 к 1
В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.
Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:
Пример 2
Найдите отношение 15 к 12
По определению посчитаем частное, а далее посмотрим на полученный результат.
Данный пример иллюстрирует, в каких случая получается смешанное число.
Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.
Мы можем прочитать результат так: 15 больше 12 в \(\mathbf<1\frac<1><4>>\) раза.
Пример 3
Найдем отношение 16 к 24.
Снова идем по алгоритму: делим первое число на второе.
В этом случае мы получили в ответе правильную дробь.
Нам это говорит о том, что первое число меньше второго.
А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в \(\mathbf<\frac<2><3>>\) раза.
Мы можем сформулировать вывод и так: 16 составляет \(\mathbf<\frac<2><3>>\) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.
Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.
Пример 4
Есть два числа, 14 и 28
Посчитаем отношение 14 к 28
И посчитаем отношение 28 к 14
Как вы видите, получились разные значения.
Как можно заметить, это взаимно обратные числа.
Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.
Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.
Пример 5
Дано, что отношение числа a к числу b равно \(\mathbf<\frac<2><5>>\), найдем отношение b к a
Для этого надо найти обратное число к \(\mathbf<\frac<2><5>>\)
Значит, отношение b к a равняется \(\mathbf<2\frac<1><2>>\)
В конце этой части добавим еще одно простое, но важное свойство.
Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.
Это легко доказать, показав, что при делении этот множитель сократится.
Пример 6
Отношение числа 10 к числу 30 равно \(\mathbf<\frac<1><3>>\)
Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно \(\mathbf<\frac<1><3>>\)
Пройти тест и получить оценку можно после входа или регистрации
Отношение и часть от числа
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него \(\mathbf<\frac<3><8>>\)
Перемножив, мы получим:
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна \(\mathbf<2\frac<1><2>>\)
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
Ответ: дробь, взяв которую от 10 получили \(\mathbf<2\frac<1><2>>\), равняется \(\mathbf<\frac<1><4>>\)
Пример 2
Отношение первого числа ко второму равно \(\mathbf<1\frac<1><5>>\), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к \(\mathbf<1\frac<1><5>>\)
Теперь можно найти второе число, домножим первое на эту дробь:
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно \(\mathbf<1\frac<1><2>>\)
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
Ответ: число a равняется 12
Пройти тест и получить оценку можно после входа или регистрации
Отношения в задачах
Теперь научимся находить отношения в задачах.
Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.
Задача 1
Длина улицы составляет 25 километров. Освещено 15 километров улицы.
а) Найдите, какая часть улицы освещена.
б) Во сколько раз вся улица длиннее ее освещенной части?
Решение:
В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.
Именно это и спрашивается в первом вопросе.
Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:
Значит, длина освещенного участка составляет \(\mathbf<\frac<3><5>>\) от длины всей улицы.
Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:
Что отвечает на вопрос второго пункта.
Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.
То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.
Задача 2
Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.
Найдите, какую часть от массы груза составляет масса одежды.
Решение:
Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.
Теперь найдем искомое отношение:
Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.
Пройти тест и получить оценку можно после входа или регистрации
Интересная информация
Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Отношение чисел
Отношения чисел: определение, свойства, виды
Определение
Отношением пары чисел называют результат их деления одно на другое. То есть понятия частного и отношения являются синонимами, обозначая одно и то же понятие. При этом число, которое делят, называют предыдущим членом, а число, на которое осуществляется деление, – последующим.
Для обозначения отношения чисел используется знак деления «:» либо черта дроби.
Общая форма записи отношения чисел: a : b или, соответственно, 
. В таких записях a – предыдущий член отношения, b – последующий. Обязательное условие для всякого отношения: 
.
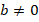
3:2
Здесь 3 и 4 – предыдущие члены отношений, 2 и 9 – последующие.
Свойства отношений
Свойство №1. Членами всякого отношения могут быть как целые, так и дробные, рациональные или другие числа.
Примеры отношений, члены которых являются целыми числами, приведены выше (см. Пример №1).
Пример №2. Отношения, члены которого дробные числа:
Свойство №2. Если члены отношения умножить (либо разделить) на одно и то же число, то его значение не изменится. Это свойство называют основным для отношений чисел.
Деление членов отношения на одно и то же число называют сокращением отношения.
Это свойство нередко используется для перехода от нецелых членов отношения к целым, что более удобно для расчетов.
Свойство №3. В отношении могут участвовать и более 2-х членов. Так, в прикладных задачах нередко используются пропорциональные величины, значения которых выражаются как раз через их отношения. Количество членов при этом может быть произвольным и равняться трем, четырем и так далее. В общем виде такие отношения записываются как a:b:c:d:…n и читаются так: «величины относятся между собой как a, b, c…»
Пример №4. Имеется треугольник, длины сторон которого относятся как 3:4:5.
Пример №5. Даны 4 пропорциональных числа, которые относятся между собой как 1:2:4:5.
В задачах, в которых приведены такого рода отношения, обычно вводится коэффициент пропорциональности и, используя свойства объекта, для которого они приведены, и (или) данные из условия, по заданному отношению находят абсолютные значения величин для этого объекта. При этом под абсолютными величинами понимают величины, выраженные в конкретных единицах измерения – кг, км и так далее.
Процентное отношение
Процентное отношение – это характерное и одно из наиболее распространенных направлений прикладного использования отношения чисел. Обозначение процентного отношения – % (процент). 1 % – это сотая часть от целого.
Процентное отношение основывается на обычном отношении, которое множат на 100. Процентное отношение показывает часть объекта (величины) в сравнении с его 100 частями, которые принимаются за целое.
Где a – часть целого, выраженная в единицах измерения, b – значение целого, выраженное в тех же единицах, z – количество процентов, которое составляет данная часть от целого.
Пример №6. На книжной полке 80 книг. Сколько процентов от этого количества составляют 36 книг?
Обозначим искомую величину через х. Тогда получаем:
Пример №7. Фермер посеял пшеницу на 2 га, что составляет 80 % от всех его посевных площадей. Какова общая посевная площадь, которой он располагает?
Обозначим искомую величину через х. Составим процентное отношение на основании данных задачи:
Нередко вместо понятия процентного отношения используют понятие долей. В этом случае целое абстрактно принимается за 1, а понятие процента не используется. Доля (часть) от данного целого в такой ситуации – это всегда будет величина, меньшая 1. Для определения доли (части) от целого используется обычное отношение:
Где b – часть от целого, c – величина целого, a – доля, которую b составляет от c.
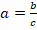
Специальной единицы измерения доля не имеет и измеряется просто в единицах.
Пример №8. Какую долю тиража изданной книги удалось продать писателю, если тираж составляет 10 тысяч экземпляров, а приобретено было 6830 книг?
Обозначим искомую величину через х. Составим отношение и найдем х:
Переход от долей к процентам предельно прост: достаточно умножить долю на 100. Так, в предыдущем примере 0,683 по отношению к общему тиражу составит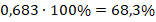 
.
Пример №9. С 1 га планировалось собрать 40 тонн картофеля. Реальная урожайность составила 0,7 от планируемой. Сколько тонн картофеля собрали?
Обозначим искомую величину через х. Составим выражение для расчета реальной урожайности и найдем х:
Пропорция
Пропорцией называют равенство двух числовых отношений. В общем виде такое равенство записывают как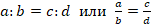 
, где a и d называют крайними членами пропорции, b и c – средними. Прочтение пропорции: отношение a к b равно отношению c к d, или a относится к b как c к d, или a во столько раз больше b во сколько больше d.
Пример №9. Примеры конкретных пропорций:
При решении практических задач с использованием отношений в виде пропорции чаще всего от деления переходят к умножению ее членов. Для этого используют основное ее свойство.
Основное свойство пропорции: произведение ее крайних членов равно произведению средних. Математически это свойство записывается так:
Если провести дальнейшие вычисления, то в итоге мы должны прийти к равенству чисел слева и справа. А именно:
Отсюда следует важная особенность: основное свойство применяют для проверки истинности составленной пропорции. Если в результате числовых преобразований получено верное равенство, то это означает, что исходные 4 числа действительно могут составить пропорцию.
Когда один из членов пропорции неизвестен и требуется найти его, то применяют правило: для вычисления неизвестного крайнего (среднего) члена перемножают средние (крайние) и делят полученное произведение на известный крайний (средний) член.
Математически это выражается так:
То есть для определения неизвестного члена перемножают пару соответствующих известных и делят их на тот известный член, который не имеет известной пары.
Отношение чисел. 6 класс
В разработке введено понятие отношения чисел, приведены примеры и задания для самостоятельного решения.
Просмотр содержимого документа
«Отношение чисел. 6 класс»
Отношения чисел (выражений)
В математике встречаются разные названия одного и того же математического действия – деления. Мы уже знаем, что результат деления называется частным двух чисел, знаем, что деление можно записать обыкновенной дробью. И сейчас мы рассмотрим ещё одно понятие – отношение двух чисел (или выражений).
Отношением двух чисел (или выражений) называется частное этих двух чисел (или выражений).
Пример 1. Отношение числа 28 к числу 7 записывается так: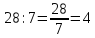 
и это означает, что число 28 больше числа 7 в 4 раза.
Пример 2. Отношение числа 5 к числу 75 записывается так: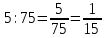 
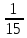
и это означает, что число 5 составляет 
часть числа 75.
во сколько раз первое число (выражение) больше второго;
какую часть одно число (выражение) составляет от другого.
Понятие отношения используется не только для чисел, но и для выражений, и для единиц измерения.
Пример 3. Найти отношение выражений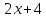 
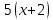
и 
.
Составим это отношение: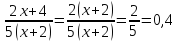 
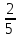
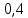
. Значит, данное отношение равно 
или 
.
Пример 4. Найти отношение веса кошки к весу котёнка, если вес кошки 5 кг, а вес котёнка 1 кг 500 г.
Для составления такого отношения, необходимо сначала привести их вес к одной единице измерения.
1 кг 500 г = 1,5 кг, тогда: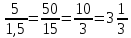 
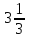
. Значит, кошка весит в 
раза больше, чем котёнок.
Ответ:
Часто отношение выражают в процентах.
Пример 5. Из 20 учеников класса 3 отличника. Какой процент всех учеников класса составляют отличники?
Составим отношение отличников ко всем ученикам класса и умножим его на 100%: 
Примеры отношения величин.
скорость – это отношение расстояния ко времени, за которое оно пройдено;
производительность труда – это отношение объёма работы ко времени, за которое она выполнена;
цена – это отношение стоимости товара к его количеству;
масштаб – это отношение длины отрезка на карте к соответствующему расстоянию на местности;
урожайность – это отношение массы собранного урожая к общей площади полей, с которой он собран.
В магазин привезли 2,4 т груш и 3,6 т яблок. Во сколько раз больше привезли яблок, чем груш? Какую часть привезённых фруктов составляли груши? Сколько процентов от всех привезённых фруктов составляют яблоки?
Из 150 кг свежих вишен получилось 36 кг сушёных. Сколько процентов сушёных вишен получается из свежих?
Ещё недавно с каждого гектара собирали 35 ц пшеницы. Теперь урожайность повысилась и стала равной 42 ц с гектара. На сколько процентов повысилась урожайность пшеницы?
Производительность первого станка-автомата 220 деталей в час, а второго 176 деталей в час. На сколько процентов производительности второго станка меньше, чем первого?
В составе товарного поезда 100 вагонов, причём крытых вагонов 35, цистерн 25, а остальные вагоны – платформы. Во сколько раз платформ больше, чем цистерн? Сколько процентов всего состава составляют платформы?
В посёлке 224 дома. Двухэтажных домов 84, а остальные дома – одноэтажные. Сколько процентов всех домов составляют одноэтажные дома?
Стоимость товара увеличилась с 200 тыс. рублей до 230 тыс. рублей. На сколько процентов увеличилась стоимость товара?
Стоимость товара увеличилась с 200 тыс. рублей до 230 тыс. рублей. На сколько процентов прежняя стоимость была меньше по сравнению с настоящей?
Купили 1,8 кг карамели и 1,2 кг ирисок. Во сколько раз меньше купили ирисок, чем карамели? Какую часть купленных конфет составляли ириски? Сколько процентов составляет карамель от общей массы купленных конфет?
Из 40 изделий, выпускаемых фабрикой, 15 изделий новой модели. Сколько процентов выпускаемых изделий составляют изделия новой модели?
При обработке заготовки её масса уменьшилась со 120 кг до 105 кг. На сколько процентов уменьшилась масса заготовки?
Высота растения увеличилась с 1,2 дм до 1,5 дм. На сколько процентов увеличилась высота растения?
Участок земли разделён на три части. Одну часть, площадью 6 а, занимает сад, вторую часть, площадью 15 а, занимает огород, а остальная часть, площадью 3 а, отведена под дом и хозяйственные постройки. Какую часть всего участка занимает сад? Во сколько раз площадь огорода больше площади сада? Сколько процентов участка занимают дом и хозяйственные постройки?
Масса ящика с товаром 11,5 кг. Масса товара 9,2 кг. Сколько процентов масса пустого ящика составляет от массы ящика с товаром?
Цена товара понизилась с 4,4 тыс. рублей до 3,74 тыс. рублей. На сколько процентов понизилась цена товара?
Цена товара понизилась с 3,51 тыс. рублей до 3,25 тыс. рублей. На сколько процентов прежняя цена товара была больше по сравнению с настоящей ценой?
На зиму заготовили 2,4 м 3 берёзовых и 1,6 м 3 еловых дров. Во сколько раз берёзовых дров заготовили больше, чем еловых? Какую часть всех дров составляют берёзовые дрова? Сколько процентов всех заготовленных дров составляют еловые дрова?
Из 40 участников шахматного турнира 9 человек имели звание гроссмейстера. Сколько процентов участников турнира составляли гроссмейстеры?
В прошлом году с каждого гектара поля собрали 32 ц зерна, а в этом году 40 ц. На сколько процентов повысилась урожайность?
Масса детали в результате обработки снизилась с 2,5 кг до 2,2 кг. На сколько процентов снизилась масса детали?
Бригада планировала отремонтировать за день 1200 м дороги. До обеда было отремонтировано 750 м, а после обеда – лишь 240 м. Какая часть дороги отремонтирована до обеда? Во сколько раз после обеда отремонтировано меньше, чем до обеда? Сколько процентов дороги осталось неотремонтированной?
Банка с вареньем стоит 120 рублей. Сколько процентов стоимость варенья составляет от стоимости банки с вареньем, если пустая банка стоит 1,5 рубля?
Цена товара повысилась с 5,2 тыс. рублей до 5,33 тыс. рублей. На сколько процентов повысилась цена товара?
Цена товара повысилась с 4,41 тыс. рублей до 4,5 тыс. рублей. На сколько процентов прежняя цена товара была меньше по сравнению с настоящей ценой?
Чтобы дойти от станции до садового участка, нужно идти 1,8 км по шоссе, 1,2 км лесом и 1 км полем. Какую часть всей дороги составляет путь, который нужно пройти полем? Сколько процентов составляет путь по шоссе и путь, который идёт лесом, от всего пути до садового участка?
По плану должны были построить 750 квартир, а построили 855. Сколько процентов плана было выполнено?
Платье стоило 3200 рублей. Через некоторое время оно стало стоить 2400 рублей. На сколько процентов снизили цену на платье?
В результате замены некоторых деталей удалось увеличить мощность двигателя, но при этом, его масса увеличилась с 66 кг до 75,57 кг. На сколько процентов увеличилась масса двигателя?
Книга в переплёте стоит 1200 рублей. Сколько процентов цена переплёта составляет от цены книги в переплёте, если книга без переплёта стоит 900 рублей?
После реконструкции станка рабочий стал изготавливать на нём за смену 252 детали вместо 240. На сколько процентов увеличилась производительность труда рабочего?
После реконструкции станка рабочий стал изготавливать на нём за смену 250 деталей вместо 235. На сколько процентов производительность труда была раньше ниже по сравнению с настоящей?
Определить процент соли в растворе, если в 400 г раствора содержится 32 г соли.
Папа, мама и сын поехали навестить бабушку. Общее расстояние, которое им надо было проехать 1300 км. Через 325 км они остановились перекусить в придорожном кафе. Какую часть пути им осталось проехать?
В компьютерной игре Сталкер 3 карты. На каждой карте 70 заданий. Мальчик выполнил 147 заданий. Какую часть игры он прошёл? Ответ запишите в виде десятичной дроби.
Общий объём флэшки составляет 2 гигабайта. (1 гигабайт = 1000 мегабайт) На неё уже записали 200 мегабайт информации. Какая часть флэшки ещё остаётся свободной?
На дачном участке 12 яблонь. Средством от вредителей обработали 4 дерева. Какая часть деревьев обработана?
В книге 325 страниц. Прочитано 75 страниц. Какую часть книги осталось прочитать?