Что такое отношение углов в геометрии
О многоугольнике с тремя сторонами
Соотношение углов и сторон в треугольнике интуитивно можно понять, если хорошо представлять эту фигуру. Речь идет о плоском объекте, который состоит всего из трех отрезков. Они расположены таким образом, что начало первого совпадает с концом последнего, то есть они пересекаются. Каждый отрезок представляет собой независимую сторону фигуры. Точка пересечения является вершиной, а соответствующий ей угол является внутренним.
Таким образом, два ключевых элемента образуют рассматриваемую фигуру:
И вершин, и сторон в любом треугольнике по три, поэтому его принято обозначать большими латинскими буквами, например, ABC или MNK. Малые буквы резервируют для обозначения длин сторон, например, a, b, c.
На первый взгляд может показаться, что рассматриваемый объект является несложным, и в нем нечего изучать. Действительно, он является самым простым по построению многоугольником, однако, он обладает большим количеством свойств, количественное и качественное знание которых требуют понимания многих теорем.
Существование фигуры
Пусть имеется три отрезка, и необходимо понять, возможно ли из них построить треугольник. Это можно сделать с помощью одного простого правила, которое можно сформулировать следующим образом: любая сторона треугольника всегда меньше суммы длин двух других.
Знание этого правила является очень важным и эффективным инструментом при решении задач. Например, из отрезков с условными длинами 1, 2 и 4 построить треугольник невозможно, а из 2, 3, 4 это сделать можно.
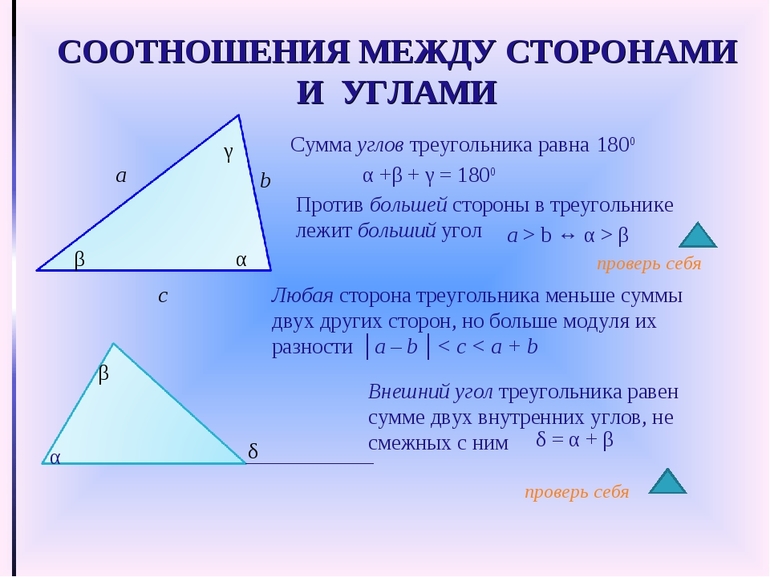
Помимо соотношения длин сторон существует также еще одна теорема, которая гласит, что во всяком треугольнике сумма его внутренних углов всегда равна 180 °. Благодаря знанию этой теоремы можно все рассматриваемые фигуры разделить на три типа:
Полноты ради следует сказать о вырожденных фигурах. К ним относятся такие многоугольники, у которых тупой стремится к 180 °. Несложно представить, что в этом случае два других будут обращаться в ноль, а сумма противолежащих им сторон окажется равной длине отрезка, расположенного напротив тупого угла. На плоскости вырожденный треугольник представляет отрезок, его площадь стремится к нулю.
Важные линии
Несмотря на всю простоту построения треугольника, при решении задач могут понадобиться дополнительные отрезки. Внутри фигуры существует целая гамма типов этих отрезков, наиболее важными из них являются следующие:
Для правильных, равнобедренных и прямоугольных треугольников некоторые из названных отрезков могут совпадать друг с другом, а также со сторонами фигуры. Например, в прямоугольном треугольнике две малые стороны (катеты) также являются высотами.
Соотношение отрезков и углов
Задачи на соотношение отрезков и угловых мер в рассматриваемой фигуре могут требовать либо качественный, либо количественный ответ. В первом случае следует провести определенное доказательство, опираясь на известные аксиомы и теоремы о сторонах треугольника и их следствия. Во втором же случае следует пользоваться формулами и выражениями, которые содержат тригонометрические функции. В действительности оба типа задач связаны между собой. Так, прежде чем использовать какую-либо формулу, следует доказать возможность ее применения в конкретной ситуации.
Большие и меньшие длины
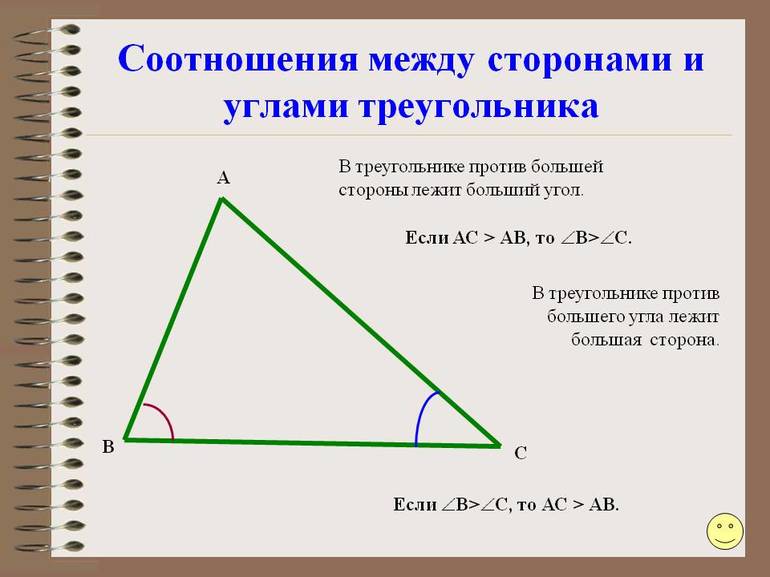
Основная теорема о соотношении между элементами в рассматриваемом типе многоугольников гласит, что против большего угла лежит большая сторона. Ее доказательство провести несложно, если построить треугольник, например, тупоугольный. Из тупого провести отрезок к противоположной стороне таким образом, чтобы он образовывал новый равнобедренный треугольник внутри исходного. После этого следует воспользоваться тем свойством, что внешний угол треугольника всегда больше внутреннего.
Следуя условию равенства углов в построенном равнобедренном треугольнике, легко показать, что против тупого всегда находится самый длинный отрезок.
Обратно эта теорема также справедлива, то есть против большей стороны треугольника лежит больший угол. Ее справедливость понятна каждому школьнику на интуитивном уровне, а доказательство заключается в переборе возможных трех вариантов соотношения между отрезками (больше, меньше, равно) и в привлечении уже доказанной теоремы.
Рассмотренные теоремы приводят к двум важным следствиям:
Рассмотренные теоремы и их следствия активно используются при изучении подобных фигур. Поскольку напротив равных углов двух треугольников лежат соответствующие им длины отрезков, то последние будут попарно относиться друг к другу с определенным коэффициентом подобия.
Теоремы косинусов и синусов
Количественной характеристикой соотношения сторон и углов являются знаменитые формулы, содержащие зависимость длин отрезков и угловых мер. Первая из них называется теоремой косинусов. Соответствующая формула имеет вид:
c 2 = a 2 + b 2 — 2*a*b*cos©.
Здесь величины a, b, c — это длины, C — угол напротив стороны c. Формула позволяет вычислить третью сторону по известным двум другим и углу между ними. Однако, возможности выражения шире, с его помощью можно посчитать всякий внутренний угол фигуры, если известны три ее стороны.
Следующая по счету, но не по важности теорема синусов. Ее математическое выражение записывается так:
a/sin (A) = b/sin (B) = c/sin©.
Эти равенства говорят о том, что отношение стороны к синусу противоположного ей угла является постоянной характеристикой конкретного треугольника. Зная связь двух углов и стороны или двух отрезков и одного угла можно рассчитать все остальные характеристики фигуры. Следует запомнить, что для любого рассматриваемого типа многоугольников однозначное вычисление всех его свойств требует знания минимум трех элементов (кроме трех углов).
Прямоугольный треугольник
Этот особый случай следует рассмотреть подробнее. Каждый школьник знает знаменитую теорему, позволяющую сравнить соответствие отрезков друг другу в этом типе фигуры. Она гласит, что сумма квадратов катетов соответствует квадрату гипотенузы, и называется пифагоровой теоремой, то есть можно записать:
Работать с прямоугольными треугольниками удобно по одной простой причине: через их геометрические параметры вводятся в математику тригонометрические функции. Последние легко использовать при вычислении сторон и углов фигуры. Например, если фигура является не только прямоугольной, но и равнобедренной, то ее катеты равны, а углы напротив них составляют по 45 °. При этом любой из катетов всегда в 2 0,5 раза меньше гипотенузы:
Это соотношение можно получить также из теоремы Пифагора.
Другая ситуация, когда один из острых углов равен 30 °. Для лежащего напротив него катета a можно записать следующее выражение:
Иными словами, лежащий против 30 ° катет составляет ровно половину длины гипотенузы.
Таким образом, в любом треугольнике существует прямая пропорциональность между длиной стороны и противолежащим ей углом. Для количественного решения задач по геометрии с этой фигурой следует пользоваться выражениями синусов, косинусов и теоремой Пифагора.
Углы и градусы
Определение величин углов
Первые попытки древних людей измерять земельные участки
(изначально геометрия – это измерение земли) наткнулись на
острую необходимость в угловых измерениях. Крайне редко
их наделы имели правильную форму. Поэтому понятие угла
появилось практически одновременно с линейным отрезком
и/или расстоянием. Другое дело, измерять и тем более
вычислять значения углов люди научились значительно позже.
Хотя уже древние греки оперировали этими понятиями более чем успешно.
Полупрямая (луч) в геометрии определяется как бесконечно длинная
прямая, имеющая начало. Она состоит из всего множества точек,
лежащих на этой линии, включая начальную. Угол же образуют два
луча с совмещенными точками начала. Можно дать и такое
определение этой геометрической фигуры. Причем общую для лучей
точку принято называть вершиной угла, а лучи – сторонами угла.
Удивительно, но размещение точки в любом месте любой прямой
эквивалентно получению двух равновеликих и разнонаправленных
лучей с общим началом. Следовательно, эта нехитрая операция
создает угол как геометрическую фигуру.
Откуда взялся градус
Достоверное происхождение этой угловой меры неизвестно.
Наиболее вероятная гипотеза о делении на 60 частей
угла равностороннего треугольника вавилонянами отлично
согласуется с шести десятеричной системой счисления, принятой
в этом архаичном обществе. Число 60 делится на 2, 3, 5, 6, 10,
15, 30 и, собственно, на 60. Отсюда удобство его применения в
торговле и прочих бытовых отношениях.
Согласно другой версии, окружность разделили на 360 равных
фрагментов по причине равенства их количества числу дней в году.
Персы, например, немало повлиявшие на развитие математики в
целом и геометрии в частности, использовали именно такой календарь.
В любом случае градус используется до сих пор, обозначая 1/360 часть
полного оборота (делит круг на 360 равных секторов). Само слово с
латыни переводится как шаг, ступень, порог. Отсюда слово градуировка,
применимое абсолютно ко всем измерительным приборам.
Для измерения более мелких величин углов используют минуту
и секунду. Эти величины также являются результатом дробления
на 60. Минута делит градус, а секунда минуту. То есть 1 минута
равна 1/60 градуса, а секунда составляет 1/60 минуты или 1/3600 градуса.
Транспортир, знакомый каждому со школьных времен – элементарнейший
инструмент, позволяющий довольно точно измерять или рисовать углы.
Разумеется, в практике промышленности, строительства и других сферах
человеческой деятельности применяются более точные средства,
теодолит, как вариант. Но результат измерения любого современного
инструмента всегда выражается в градусах.
Учитывая простоту фигуры и ее составляющих, углы не отличаются
большим разнообразием. Принято выделять следующие их виды:
Помимо прямого, существует еще несколько частных случаев, а именно:
Геометрия, оставаясь неотъемлемой частью математики,
все же выделена в отдельную дисциплину. Причина
такого подразделения проста. Математическая наука
не терпит даже тени хаоса, что выражается в четкой
классификации ее разделов, но с сохранением
органической связи между собой.
На самом деле, без глубокого знания основ геометрии
практически невозможно изучить смежные математические
дисциплины, такие как тригонометрия, анализ, интегральное
или дифференциальное счисления. Более того, изучение
любой точной науки требует свободного владения
геометрическими понятиями. Механика или оптика
в физике – наиболее яркое тому подтверждение.
Геометрия. Урок 2. Углы
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Понятие угла
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Стороны угла – лучи, которые образуют угол.
Вершина угла – точка, из которой выходят лучи.
Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
Виды углов:
Биссектриса угла
Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.
∠ A O D = ∠ B O D = ∠ A O B 2
Углы, образованные при пересечении двух прямых
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.
По свойству вертикальных углов:
∠ C O D = ∠ A O B
∠ B O D = ∠ A O C
( 1 ) и ( 2 )
( 2 ) и ( 3 )
( 3 ) и ( 4 )
( 4 ) и ( 1 )
По свойству смежных углов:
∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 °
Углы, образованные при пересечении двух прямых секущей
Прямая, пересекающая две заданные прямые, называется секущей этих прямых.
Существует пять видов углов, которые образуются при пересечении двух прямых секущей.
( 1 ) и ( 5 )
( 2 ) и ( 6 )
( 3 ) и ( 7 )
( 4 ) и ( 8 )
Сумма углов многоугольника
Сумма углов произвольного n -угольника вычисляется по формуле:
Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °
Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °
Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °
Так можно продолжать до бесконечности.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунках изображены примеры правильных многоугольников:

α n = 180 ° ⋅ ( n − 2 ) n
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с углами
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.