Что такое отношение в геометрии

Основные отношения школьной геометрии

Использование алгебраического метода основывается на связях между элементами фигур. Из школьного курса известно, что:

· сумма смежных углов равна 180 ;

· вертикальные углы равны;

· в равнобедренном треугольнике углы при основании равны;

· если в треугольнике два угла равны, то стороны против них также равны;

· в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;

· сумма углов треугольника равна 180 ;

· внешний угол треугольника равен сумме внутренних углов, не смежных с ним;

· серединные перпендикуляры к сторонам треугольника пересекаются в одной точке – центре описанной около этого треугольника окружности;

· биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанной в этот треугольник окружности;

· при пересечении двух прямых а и b третьей прямой с внутренние накрест лежащие углы равны тогда и только тогда, когда а || b;

· противоположные стороны выпуклого четырёхугольника равны тогда и только тогда, когда этот четырёхугольник – параллелограмм;

· диогонали четырёхугольника точкой пересечения делятся пополам тогда и только тогда, когда этот четырёхугольник – параллелограмм;

· параллелограмм имеет равные диагонали тогда и только тогда, когда он – прямоугольник;

· параллелограмм имеет взаимно перпендикулярные диагонали тогда и только тогда, когда он – ромб;

· если на одной стороне угла параллельные прямые отсекают равные отрезки, то при пересечении их с другой стороной угла также возникают равные отрезки (теорема Фалеса);

· средняя линия треугольника параллельна третьей стороне и равна её половине;

· средняя линия трапеции параллельна основаниям и равна их полусумме;

· параллельные прямые отсекают на сторонах угла пропорциональные отрезки;

· в треугольнике квадрат большей стороны равен сумме квадратов двух других сторон тогда и только тогда, когда этот треугольник прямоугольный;

· для любых трёх точек А, В, С, лежащих на одной прямой, АВ = АС + СВ или АВ = АС – СВ;

· центральный угол окружности измеряется дугой, на которую опирается;

· вписанный в окружность угол измеряется половиной дуги, на которую опирается;

· произведение частей хорды, на которые она делится своей точкой М, одно и то же для всех хорд, проведённых через М;

· произведение секущей, проведённой через точку М, находящуюся вне окружности, на её внешнюю часть одно и то же для всех секущих, проведённых через М;

· квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними (теорема косинусов);

· стороны треугольника пропорциональны синусам противолежащих углов (теорема синусов);

· в треугольнике против большего угла лежит большая сторона;

· в треугольнике против большей стороны лежит больший угол;

· отношение длины окружности к её диаметру есть величина постоянная (константа), она обозначается p;

· для вычисления площадьи S некоторых фигур применяют формулы:

S_{треугольника} = аh, где а – сторона треугольника, h – высота к ней;

S_{треугольника} = аb sіnÐC, где а и b – стороны треугольника, С –угол между ними;

S_{треугольника} = , где а, b, c – стороны треугольника,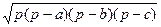

р = (а+b+c) –его полупериметр;

S_{трапеции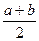} = h, где а и b – основания трапеции, h – проведённая к ним высота;

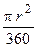
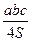
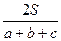
S_{сектора} = a, где r – радиус сектора, a – его градусная мера;

· R = , r = , a, b, c – стороны треугольника, S – его площадь, R и r – радиусы описанной около него и вписанной в него окружностей соответственно;

· площади подобных фигур относятся как квадраты их линейных размеров;

· S_пр = S₀ cos j, где S₀ – площадь фигуры Ф, размещённой в плоскости a, S_пр – площадь ортогональной проекции фигуры Ф на плоскость b, j – двугранный угол между плоскостями a и b;

· противолежащие грани параллелепипеда параллельны и равны;

· диагонали параллелепипеда пересекаются в одной точке и делятся ей пополам;

· квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений;

· для вычисления боковых поверхностей тел применяются формулы:

§ S_{бок. конуса} = p rl, где r – радиус основания конуса, l – его образующая;

· для вычисления объёмов тел применяют следующие формулы:

§ V_{пирамиды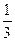} = S_осн.Н, где S_осн. – площадь основания пирамиды, Н – её высота;

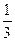
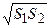
§ V_{усеч. пирамиды} = _. Н (S₁ + S₂ + ), где H – высота усечённой пирамиды, S₁, S₂ – площади её оснований;

§ V_конуса = 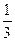_. p r 2 Н, где r – радиус основания конуса, H – его высота;

§ V_{усеч. конуса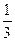} = _. pН (r₁ 2 + r₁ r₂+r₂ 2 ), где H – высота усечённого конуса, r₁ и r₂ – радиусы его оснований;

§ V_{шар. сегмента} = p Н 2 (R – 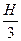), где R – радиус сегмента, H – его высота;

§ V_{шар. сектора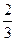} = pR 2 Н, где R – радиус сектора, H – высота соответствующего шарового сегмента;

· объёмы подобных тел относятся как кубы их линейных размеров.

Источник

Что такое пропорция

Что такое пропорция

Пропорция — это равенство двух отношения.

Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.

Пропорция всегда содержит равные коэффициенты.

Если выразить определение формулой, то выглядеть оно будет так:

a и d — крайние члены пропорции, b и с — средние члены пропорции.

Читается это выражение так: a так относится к b, как c относится к d

Например:

Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.

15 и 3 — крайние члены пропорции.

5 и 9 — средние члены пропорции.

Наглядный пример для понимания:

У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.

Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!

А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.

Что мы имеем: 4 кусочка и 2 друга, претендующих на них.

Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.

Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.

Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉

Основное свойство пропорции

Запомните основное свойство пропорции:

Произведение крайних членов пропорции равно произведению средних членов этой пропорции.

В виде формулы свойство выглядит так:

a : b = c : d
a * d = b * c

Мы знаем, что a и d — крайние члены пропорции, b и c — средние.

Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.

Давайте проверим несколько пропорций.

Пример 1. Дана пропорция:6/2 = 12/4

Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.

Пример 2. Дана пропорция: 10/2 = 16/4

Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Примеры решения задач с пропорцией

Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.

Задачка 1. Дана математическая пропорция: 15/3 = x/4

Ответ: в пропорции 15/3 = x/4, x = 20

Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.

Ответ: четвертый член пропорции — 12.

Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?

Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.

Задачка 4. Дана пропорция: 20/2 = y/4

Источник

Геометрия

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Знакомство с геометрией

Вот и настал момент прощания с математикой, сопровождающей нас на протяжении долгих шести лет школьной жизни. Но огорчаться не нужно, на смену привычной математике приходят занимательные и интересные разделы этой науки – алгебра и геометрия.

Давайте разберемся, что же такое геометрия, для чего она нужна, где её используют?

В дословном переводе с греческого, геометрия означает землемерие:

Более точное определение утверждает, что наука об отношениях плоскостей, пространств и изучении форм называется геометрией.

Геометрия содержит ряд основных понятий, необходимых для дальнейшего изучения и применения на практике геометрических знаний. Давайте познакомимся с ними поближе.

Основные понятия геометрии

Понятие точки

Фигура, которую невозможно измерить, а для вычислений используется только место её расположения, называется точкой. Такие фигуры обозначают цифрами и буквами латиницы. Если точек много, то обозначения должны быть разными.

Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

Читается: точка A, точка B, точка C

Понятие линии

Линия представляет собой массу точек. Линии принято обозначать строчными буквами латиницы.

Источник

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Данные определения даны для острого угла прямоугольного треугольника!

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Угол поворота

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Синус (sin) угла поворота

При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Основные функции тригонометрии

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Источник

Геометрия

Полезное

Смотреть что такое «Геометрия» в других словарях:

ГЕОМЕТРИЯ — (греч. geometria, от ge земля, и metron мера). Часть математики, имеющая предметом свойства и измерения линий, поверхностей и объемов тел. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ГЕОМЕТРИЯ греч. geometria,… … Словарь иностранных слов русского языка

ГЕОМЕТРИЯ — ГЕОМЕТРИЯ, раздел математики, предметом изучения которого являются пространственные отношения и формы. Для большинства людей геометрия ассоциируется только с ГЕОМЕТРИЕЙ ЕВКЛИДА, предметом которой являются плоскости и жесткие геометрические фигуры … Научно-технический энциклопедический словарь

ГЕОМЕТРИЯ — ГЕОМЕТРИЯ, геометрии, мн. нет, жен. (от греч. ge земля и metreo измеряю). Отдел математики, в котором изучаются пространственные формы, их измерение и взаимное расположение. Элементарная геометрия. Аналитическая геометрия (пользующаяся методами… … Толковый словарь Ушакова

ГЕОМЕТРИЯ — (от гео. и. метрия), часть математики, изучающая пространственные формы (например, фигуры и тела), их отношения (например, взаимное расположение) и их обобщения. Зарождение геометрии относится ко 2 му тысячелетию до нашей эры, в… … Современная энциклопедия

ГЕОМЕТРИЯ — ГЕОМЕТРИЯ, и, жен. Раздел математики, изучающий пространственные отношения и формы. | прил. геометрический, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

геометрия — сущ., кол во синонимов: 9 • астероид (579) • линиолонгиметрия (2) • линиометрия (2) … Словарь синонимов

геометрия — – правильная форма авто. EdwART. Словарь автомобильного жаргона, 2009 … Автомобильный словарь

геометрия — конфигурация геометрическая форма — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы конфигурациягеометрическая форма EN geometry … Справочник технического переводчика

Источник