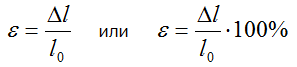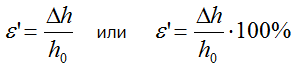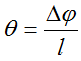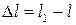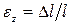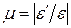Что такое относительная поперечная деформация

Сопротивление материалов. Шпаргалка для студентов

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

Оглавление

Приведённый ознакомительный фрагмент книги Сопротивление материалов. Шпаргалка для студентов предоставлен нашим книжным партнёром — компанией ЛитРес.

5. Деформации при растяжении и сжатии. Закон Гука. Коэффициент поперечной деформации

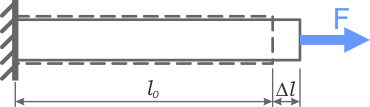
Некоторые элементы конструкций и элементов подвергаются только продольным нагрузкам, что вызывает в них деформацию растяжения или сжатия. Длина стержня, подвергнутого растяжению, увеличивается, а площадь его поперечного сечения уменьшается. При сжатии наоборот — длина уменьшается, а площадь сечения увеличивается. При этом изменение длины называют линейной продольной деформацией, а изменение площади поперечного сечения — поперечной линейной деформацией. Для оценки интенсивности деформации применяют такие понятия, как относительная продольная ε и относительная поперечная ε’ — деформации, приходящиеся на единицу длины или пощади сечения стержня.

где Δl — изменение длины стержня;

Δa — изменение площади сечения.

Продольную деформацию растяжения обычно считают положительной, деформацию сжатия — отрицательной. Продольная и поперечная деформации связаны соотношением

μ — коэффициент поперечной деформации, который имеет свое значение для разных тел (в пределах упругого деформирования). Этот коэффициент называют коэффициентом Пуассона.

В пределах упругого деформирования экспериментально была установлена прямая зависимость между нормальным напряжением σ и относительной деформацией ε.

Это соотношение носит название закона Гука, а коэффициент пропорциональности E называется модулем упругости первого рода. Модуль упругости — это величина, постоянная для каждого материала. Из соотношения видно, что при постоянном напряжении деформация меньше при большем модуле упругости.

Если рассматривать участок длиной l, на котором продольная сила и площадь поперечного сечения постоянны, закон Гука можно представить в виде:

Произведение EA называется жесткостью сечения.

При растяжении или сжатии стержня его сечения перемещаются. Осевое перемещение сечений друг относительно друга равно изменению длины стержня между этими сечениями. График, на котором изображены перемещения всех сечений относительно одного, принятого за неподвижное, называется эпюром перемещений.

Источник

iSopromat.ru

Относительными называют деформации определяемые отношением изменения размера (абсолютной деформации) к соответствующим начальным размерам тела.

Другими словами относительные деформации показывают насколько изменился размер тела в сравнении с его размерами до нагружения.

Например, при растяжении (сжатии) прямого стержня его относительное удлинение ε находится отношением абсолютного удлинения Δl к начальной длине l₀.

Здесь Δh – абсолютная поперечная деформация,
Δh₀ – начальный поперечный размер (до деформации).
Измеряется в единицах или процентах [%]

При кручении — относительный угол закручивания

где, Δφ – угол закручивания участка вала,
l – длина рассматриваемого участка.

Единица измерения – радиан на метр [рад/м].

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Коэффициент Пуассона. Связь продольной и поперечной деформации

Пусть в результате деформации первоначальная длина стержня l станет равной. l1. Изменение длины

называется абсолютным удлинением стержня.

При растяжении продольная деформация считается положительной, а при сжатии – отрицательной.

Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:

.

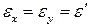
Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона или коэффициентом поперечной деформации, вычисляется по формуле:

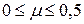
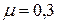
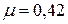
Для различных материалов коэффициент Пуассона изменяется в пределах . Например, для пробки , для каучука , для стали , для золота .

Источник

iSopromat.ru

Поперечной называют деформацию (абсолютную или относительную), которая меняет размеры сечения в направлении, перпендикулярном продольной оси бруса.

Одновременно с продольной деформацией, при действии на брус сжимающей или растягивающей силы наблюдается также поперечная деформация.

При сжатии бруса его поперечные размеры увеличиваются, а при растяжении – уменьшаются.

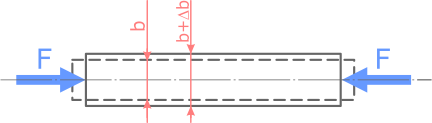
Если поперечный размер бруса до приложения к нему сжимающих сил F обозначить b, а после приложения этих сил b+Δb (рис. 1), то величина Δb будет обозначать абсолютную поперечную деформацию бруса.

Отношение Δb/b является относительной поперечной деформацией и обозначается как ε_поп.

Опыт показывает, что при напряжениях, не превышающих предела упругости относительная поперечная деформация ε_поп прямо пропорциональна относительной продольной деформации ε_пр, но имеет обратный знак:

Коэффициент пропорциональности ν зависит от материала бруса. Он называется коэффициентом поперечной деформации, или коэффициентом Пуассона, и представляет собой отношение относительной поперечной деформации к относительной продольной, взятое по абсолютной величине (модулю), т.е.

Коэффициент Пуассона ν наряду с модулем упругости Е характеризует упругие свойства материала и определяется экспериментально. Для различных материалов он изменяется от нуля (для пробкового дерева) до 0,5 (для резины, парафина).

Для металлов значения ν лежат в пределах 0,25 – 0,35.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Относительная поперечная деформация

При рас­тя­жении (сжа­тии) пря­мого бру­са кро­ме про­дольной де­фор­ма­ции e про­ис­хо­дит из­ме­нение по­переч­ных раз­ме­ров бру­са (рис. 2.5). Ши­рина бру­са при рас­тя­жении уменьша­ет­ся на Db. Ес­ли Db от­нести к пер­во­начальной ши­рине, то по­лучим вы­раже­ние для оп­ре­деле­ния от­но­сительной по­переч­ной де­фор­ма­ции e₁:

Рис. 2.5

От­но­шение от­но­сительной по­переч­ной де­фор­ма­ции к от­но­сительной про­дольной де­фор­ма­ции на­зыва­ют ко­эф­фи­ци­ен­том Пу­ас­со­на и обоз­на­ча­ют m:

Ко­эф­фи­ци­ент Пу­ас­со­на, так же как и мо­дуль уп­ру­гос­ти Е, ха­рак­те­ризу­ет фи­зичес­кие свойства ма­тери­ала; для ме­тал­лов его зна­чение ко­леб­лется в пре­делах от 0,25 до 0,35. Не­кото­рые зна­чения ко­эф­фи­ци­ен­та µ при­веде­ны в табл. 2.1.

Таблица 2.1. Механические характеристики материалов [11]

Ма­тери­ал

Нап­ря­жение, Н/мм 2

E, 10 5 Н/мм

d %, l = 5d

Сталь 30 не­зака­лен­ная330330530—2,028Сталь 30 за­кален­ная1030901100—2,011Сталь 45 не­зака­лен­ная370370620—2,024Сталь 45 за­кален­ная10409701080—2,013Сталь УВ не­зака­лен­ная250430630—2,025Сталь УВ за­кален­ная7007001 100—2,016Сталь 30ХГС за­кален­ная140014001620—2,010Сталь 40ХНВ за­кален­ная172021002050—2,010Чу­гун се­рый СЧ251403102509400,70,6—Ти­тан тех­ни­чес­кий520520600—1,123—Медь отож­женная5555220—1,146Медь прут­ко­вая250250320—1,115Ла­тунь330330450—1,217—Брон­за110110136—1,27,5—Алю­миний505084—0,730,26…0,36Ду­ралю­мин340340540—0,7513—Тек­сто­лит751151271680,031,5

Основные механические характеристики материалов

Ме­хани­чес­кие свойства ма­тери­алов ус­та­нав­ли­ва­ют опыт­ным пу­тем, ис­пы­тывая об­разцы на рас­тя­жение. За­тем ди­аг­рамму рас­тя­жения пе­рес­тра­ива­ют в ко­ор­ди­натах s—e. Как вид­но из рис. 2.6, она име­ет та­кой же вид, как и в ко­ор­ди­натах F—Dl (см. рис. 2.4), но эта кри­вая бу­дет ха­рак­те­ризо­вать уже не свойства об­разца, а свойства ма­тери­ала. От­ме­тим на этой ди­аг­рамме ха­рак­терные точ­ки.

Рис. 2.6

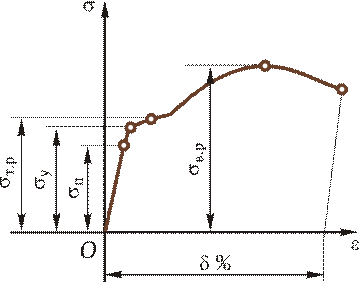
На­ибольшее зна­чение нап­ря­жения, при ко­тором спра­вед­лив за­кон Гу­ка, на­зыва­ет­ся пре­делом про­пор­ци­ональнос­ти s_п.

Уп­ру­гие свойства ма­тери­ала сох­ра­ня­ют­ся до зна­чений нап­ря­жения, на­зыва­емо­го пре­делом уп­ру­гос­ти. Под пре­делом уп­ру­гос­ти s_у по­нима­ет­ся та­кое на­ибольшее зна­чение нап­ря­жения, при ко­тором ма­тери­ал не по­луча­ет ос­та­точ­ных де­фор­ма­ций.

На прак­ти­ке пре­дел про­пор­ци­ональнос­ти и пре­дел уп­ру­гос­ти труд­но под­да­ют­ся из­ме­рению, по­это­му зна­чения s_п и s_у в спра­воч­ные дан­ные по свойствам ма­тери­алов обыч­но не вклю­ча­ют­ся.

Бо­лее оп­ре­делен­ной ха­рак­те­рис­ти­кой яв­ля­ет­ся пре­дел те­кучес­ти. Под пре­делом те­кучес­ти по­нима­ет­ся та­кое зна­чение нап­ря­жения, при ко­тором рост де­фор­ма­ции про­ис­хо­дит без за­мет­но­го уве­личе­ния наг­рузки. В тех слу­ча­ях, ког­да на ди­аг­рамме от­сутс­тву­ет яв­но вы­ражен­ная пло­щад­ка те­кучес­ти, за пре­дел те­кучес­ти ус­ловно при­нима­ют та­кое зна­чение нап­ря­жения, при ко­тором ос­та­точ­ная де­фор­ма­ция сос­тавля­ет 0,2%. В этом слу­чае ус­ловный пре­дел те­кучес­ти обоз­на­ча­ют s_0,2.

Ес­ли не­об­хо­димо от­ли­чить пре­дел те­кучес­ти при рас­тя­жении от пре­дела те­кучес­ти при сжа­тии, то в обоз­на­чение вво­дит­ся до­пол­ни­тельный ин­декс «р» или «с» (s_т.р и s_т.с).

Пре­дел те­кучес­ти лег­ко оп­ре­делить эк­спе­римен­тально, по­это­му он яв­ля­ет­ся од­ной из ос­новных ме­хани­чес­ких ха­рак­те­рис­тик ма­тери­ала.

От­но­шение мак­си­мальной си­лы, ко­торую спо­собен вы­дер­жать об­ра­зец, к его на­чальной пло­щади по­переч­но­го се­чения на­зыва­ет­ся пре­делом проч­ности, или вре­мен­ным соп­ро­тив­ле­ни­ем раз­ры­ву — s_в.р (сжа­тию — s_в.с).

Сле­ду­ет за­метить, что s_в.р не яв­ля­ет­ся тем зна­чени­ем нап­ря­жения, при ко­тором раз­ру­ша­ет­ся об­ра­зец. Фак­ти­чес­кое нап­ря­жение, при ко­тором об­ра­зец раз­ру­ша­ет­ся, бу­дет больше, так как пло­щадь по­переч­но­го се­чения в этот мо­мент меньше пер­во­начальной пло­щади вследс­твие об­ра­зова­ния шейки (нап­ря­жение, ука­зан­ное на ди­аг­рамме, под­счи­тыва­ет­ся для пер­во­начальной пло­щади по­переч­но­го се­чения об­разца). Зна­чение s_в.р яв­ля­ет­ся срав­ни­тельной ха­рак­те­рис­ти­кой проч­нос­тных свойств ма­тери­алов и час­то ис­пользу­ет­ся при рас­че­тах.

При ис­пы­тани­ях на рас­тя­жение оп­ре­деля­ют еще од­ну ха­рак­те­рис­ти­ку ма­тери­ала — так на­зыва­емое от­но­сительное уд­ли­нение при раз­ры­ве d%.

От­но­сительное уд­ли­нение при раз­ры­ве пред­став­ля­ет со­бой зна­чение сред­ней ос­та­точ­ной де­фор­ма­ции, ко­торая воз­ни­ка­ет к мо­мен­ту раз­ры­ва на оп­ре­делен­ной стан­дар­тной дли­не об­разца. За стан­дар­тную дли­ну об­разца при­нима­ют ли­бо l₀ = 10d, ли­бо l₀ = 5d, где d — ди­аметр об­разца.

Зна­чения ме­хани­чес­ких ха­рак­те­рис­тик не­кото­рых на­ибо­лее час­то встре­ча­ющих­ся ма­тери­алов при­веде­ны в табл. 2.1.

Расчеты на прочность при растяжении и сжатии

Раз­ме­ры эле­мен­тов конс­трук­ции сле­ду­ет под­би­рать так, что­бы обес­пе­чить их проч­ность при на­именьшей зат­ра­те ма­тери­ала. На ос­но­вании ана­лиза конс­трук­ции вы­яв­ля­ют точ­ку, где воз­ни­ка­ют на­ибольшие нап­ря­жения s_на­иб. Найден­ное зна­чение нап­ря­жения со­пос­тавля­ют с до­пус­ка­емым зна­чени­ем нап­ря­жения для дан­но­го ма­тери­ала и конс­трук­ции.

На ста­дии про­ек­ти­рова­ния конс­трук­ции за­да­ют­ся ко­эф­фи­ци­ен­том за­паса n. Он наз­на­ча­ет­ся из кон­крет­ных ус­ло­вий ра­боты рас­счи­тыва­емой конс­трук­ции. В каж­дой об­ласти тех­ни­ки уже сло­жились свои тра­диции, свои тре­бова­ния и спе­цифи­ка рас­че­тов. Нап­ри­мер, при про­ек­ти­рова­нии стро­ительных со­ору­жений, рас­счи­тан­ных на дол­гие сро­ки экс­плу­ата­ции, за­пасы при­нима­ют до­вольно больши­ми (n_в = 2…5). Ин­декс «в» по­казы­ва­ет, что за­пас вы­чис­ля­ют от пре­дела проч­ности s_в. В ави­аци­он­ной тех­ни­ке на конс­трук­цию нак­ла­дыва­ют­ся стро­гие ог­ра­ниче­ния по мас­се, по­это­му ко­эф­фи­ци­ен­ты за­паса так­же оп­ре­деля­ют­ся по пре­делу проч­ности, но сос­тавля­ют n_в = 1,3…2,0.

Зна­чение ко­эф­фи­ци­ен­та за­паса за­висит и от свойств ма­тери­ала. В слу­чае плас­тично­го ма­тери­ала ко­эф­фи­ци­ент за­паса бе­рет­ся от пре­дела те­кучес­ти (n_т = 1,5…2,0), а для хруп­ких ма­тери­алов за­пас рас­счи­тыва­ет­ся от пре­дела проч­ности и при­нима­ет­ся n_в = = 2,5…4,0.

Наз­на­чив ко­эф­фи­ци­ент за­паса, для дан­но­го эле­мен­та конс­трук­ции рас­счи­тыва­ют до­пус­ка­емое нап­ря­жение

оп­ре­деля­ют раз­ме­ры про­ек­ти­ру­емо­го эле­мен­та.

При­мер 2.2

Оп­ре­делить ди­амет­ры по­переч­ных се­чений бру­са (ма­тери­ал — не­зака­лен­ная сталь 30), наг­ру­жен­но­го по схе­ме, при­веден­ной на рис. 2.3, а. Си­ла F = 1000 Н.

1. Сна­чала не­об­хо­димо пос­тро­ить эпю­ры N и s. Ме­тоди­ка и пос­ле­дова­тельность пос­тро­ения эпюр пред­став­ле­ны в при­мере 2.1.

2. Оп­ре­деля­ем ко­эф­фи­ци­ент за­паса. Пос­кольку ма­тери­ал плас­тичный, при­нима­ем ко­эф­фи­ци­ент за­паса n_т = 1,5.

4. Про­ана­лизи­ровав эпю­ру нап­ря­жений (см. рис. 2.3, д), де­ла­ем вы­вод, что на двух учас­тках воз­ни­ка­ет оди­нако­вое нап­ря­жение s_на­иб = F/S. Пос­кольку дан­ный ма­тери­ал ра­бота­ет оди­нако­во на рас­тя­жение и сжа­тие, то мож­но для лю­бого из этих двух учас­тков за­писать ус­ло­вие s_на­иб £ [s]:

Источник