Что такое отрезки прямые
Что такое отрезок
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Одним из понятий геометрии, с которым знакомятся еще в начальной школе, является отрезок. Уйма задач по математике и геометрии строится на понятиях отрезка и прямой.
Понимание, что такое отрезок, поможет решать всевозможные задачи и примеры на уроках математики как в школе, так и в высших учебных заведениях.
Отрезок — это геометрическая фигура
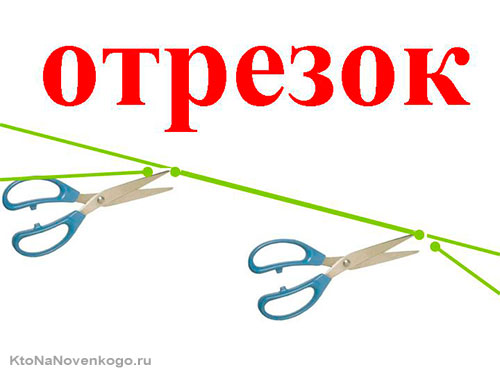
Согласно определению в словаре, отрезком называют часть прямой, ограниченную двумя точками, находящимися на ней. Именно по обозначениям этих точек и дается название отрезка.
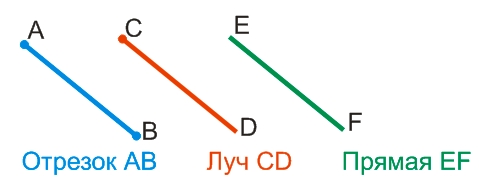
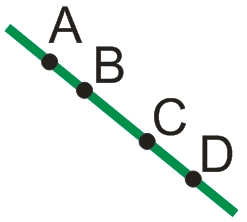
На рисунке, изображенном ниже, показан отрезок AB. Точки A и B являются концами отрезка. Длиной отрезка называют расстояние между его концами.
В математике принято обозначать точки, и соответственно отрезки, большими буквами латинского алфавита. Если нужно нарисовать отрезок, чаще всего его изображают без прямой, а лишь от одного конца до другого.
Также можно сказать, что отрезок — это совокупность всех точек, которые лежат на одной прямой и находятся между двумя заданными точками, которые являются концами данного отрезка.
Если на отрезке между его концами отметить еще одну точку, она разделит данный отрезок на два. Длину отрезка АВ можно посчитать, просуммировав длины отрезков АС и СВ.
Разница между отрезком, лучом и прямой
Школьники иногда путают понятия прямой, луча и отрезка. И вправду, эти понятия очень схожи между собой, однако имеют принципиальное различие:
Точка, находящаяся на прямой, делит ее на два луча. Количество же отрезков на одной прямой может быть бесконечным.
Чтобы различать эти фигуры на рисунке, в начале и конце рисуемой линии ставятся или не ставятся точки. Рисуя луч, точка ставится в одном конце, а изображая отрезок — в обоих концах. Прямая не имеет концов, поэтому точки в конце линии не ставятся.
Направленный отрезок — это вектор
Отрезки бывают двух видов:
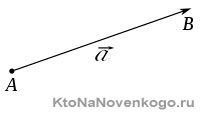
Для ненаправленных отрезков, АВ и ВА — одинаковые отрезки, так как направление не имеет значения.
Если же говорить о направленных отрезках, порядок перечисления его концов имеет решающее значение. В таком случае, АВ ➜ и ВА ➜ — разные отрезки, так как они противоположно направленные.
Направленные отрезки называются векторами. Векторы могут обозначаться как двумя заглавными буквами латинского алфавита со стрелочкой над ними, так и одной маленькой буквой со стрелочкой.
Векторы часто рассматривают в системе координат. Модуль вектора равен квадратному корню суммы квадратов координат концов вектора.
Коллинеарными векторами называются те, что лежат на одной или на параллельных прямых.
Ломаная линия — это множество соединенных отрезков
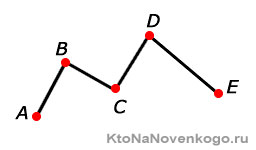
Ломаная линия состоит из множества отрезков, которые называются ее звеньями. Эти отрезки соединены друг с другом своими концами и не расположены под углом 180°.
Вершинами ломаной являются следующие точки:
Число вершин ломаной всегда на один больше, чем количество ее звеньев. Обозначается ломаная перечислением всех ее вершин начиная с одного конца и заканчивая другим.
Например, ломаная ABCDEF состоит из отрезков AB, BC, CD, DE и EF и вершин A, B, C, D, E и F. Звенья AB и BC являются смежными, так как имеют общий конец — точку В. Длина ломаной вычисляется как сумма длин всех ее звеньев.
Любая замкнутая ломаная является геометрической фигурой — многоугольником.
Сумма углов многоугольника кратна 180° и вычисляется по следующей формуле 180*(n-2), где n — количество углов или отрезков, составляющих данную фигуру.
Отрезок времени
Интересно, что слово отрезок применимо не только к геометрическим понятиям, но и как временной термин.
Отрезком времени называют период между двумя событиями, датами. Он может измеряться как секундами или минутами, так и годами или даже десятилетиями.
Время в целом в таком случае определяется как временная прямая.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (2)
Чтобы не путать с лучом, надо просто запомнить, что отрезок — это две точки. То есть эта прямая и на ней две точки — это и называется отрезком.
Это самая простая часть геометрии и надо просто внимательно читать.
Жизнь тоже можно разделить на отрезки и все они будут неотделимо связаны с временем и конкретным человеком.
Точки, Прямые и Отрезки — Определения и Свойства
Вспомним определения точки и прямой:
Точка — это фигура в геометрии, не имеющая никаких
измеримых характеристик, кроме координат.
Прямая — это фигура в геометрии, которая не
имеет ни начала, ни конца.
Для изображения прямых на чертеже используют линейку, но
при этом можно изобразить только часть прямой, а вся прямая бесконечна.
Принято обозначать прямые малыми латинскими буквами, а точки —
большими латинскими буквами.
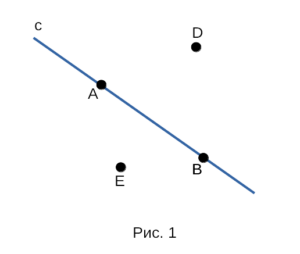
На рисунке 1 изображены прямая c и точки A, B, D, E. Точки А и B
лежат на прямой c, а точки D и E не лежат. Прямая с проходит через
точки A и B, но не проходит через точки С и D. Также заметим, что через
точки A и В нельзя провести другую прямую, не совпадающую с прямой c.
Через любые две точки можно провести прямую,
и притом только одну.
Если две прямые имеют общую точку, то можно сказать,
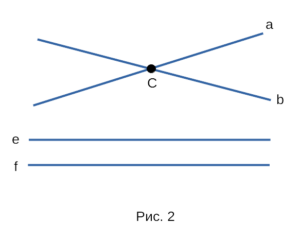
что они пересекаются. На рисунке 2 прямые a и b
пересекаются в общей точке C, а прямые e и f не
пересекаются, так как не имеют общей точки. Две прямые
не могут иметь двух и более общих точек, так как через две
и более точек проходит только одна прямая.
Две прямые имеют только одну общую точку,
либо не имеют общих точек.
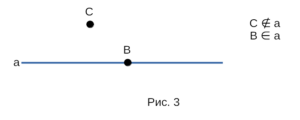
Прямую, на которой отмечены две точки, иногда обозначают двумя
буквами. Для обозначения того, лежит ли точка на прямой или нет,
используют математический символ ∈ или ∉. Пример использования
математического символа ∈ или ∉ на рисунке 3.
Часть прямой ограниченная двумя точками называется отрезком. Точки,
ограничивающие отрезок, называются концами отрезка. Отрезок имеет
начало и конец. Пример отрезка на рисунке 4.
Отрезок, луч, прямая
Раздел математики, изучающий объемные фигуры и законы их измерения, называется геометрией.
Планиметрия изучает двумерные фигуры, расположенные на плоскости.
Простейшими фигурами планиметрии являются отрезок, луч и прямая.
Всё это прямые линии, главное отличие которых друг от друга заключается в следующем:
Провести «настоящую» прямую или луч невозможно, поэтому, ограничиваются построением отрезка, а чтобы различать отрезок, луч и прямую, ставят или не ставят точку в начале и конце отрезка:
Совпадающие прямые
Две прямые, расположенные в одной плоскости, могут либо пересекаться друг с другом (иметь одну общую точку), либо не пересекаться друг с другом (не иметь общих точек).
Возьмем произвольные четыре точки A, B, C, D, расположенные в одной плоскости и лежащие на одной прямой.
Очевидно, что вторая прямая наложится на первую. Говорят, что прямые AD и BC совместились или совпали.
Совпадающие прямые не являются ни пересекающимися, ни параллельными, поскольку имеют бесконечное множество общих точек. Все же, некоторые авторы совмещенные прямые рассматривают, как частный случай параллельных прямых, что, в общем-то, недалеко от истины.
Скрещивающиеся прямые
Две прямые, имеющие одну общую точку, называются скрещивающимися.
Перпендикулярными прямыми называются две скрещивающиеся прямые, при пересечении которых образуются четыре прямых угла.
Доказать это очень просто.
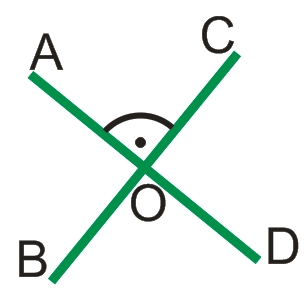
При пересечении двух прямых образуются 4 угла (см. рисунок выше): AOC, COD, DOB, BOA.
Если один из углов, например, АОС, равен 90°, то и смежный с ним угол COD также будет равен 90° (см. Что такое угол). Также будет прямым и другой смежный угол BOA.
Углы AOC и DOB также будут равны между собой, поскольку являются вертикальными углами.
Если же, какой-либо из углов (например, угол АОС) не является прямым, то прямыми не будут и смежные с ним углы COD и BOA. Поскольку, углы AOC и DOB являются вертикальными, то они равны между собой, а, т. к., угол АОС не равен 90°, то и угол DOB также не будет прямым.
Свойство перпендикулярных прямых: через любую точку плоскости можно провести тлько одну прямую, перпендикулярную данной прямой.
Параллельные прямые
Прямые будут параллельными, если они не имеют общих точек и при этом лежат в одной плоскости.
Аксиома параллельных прямых: через любую точку плоскости можно провести тлько одну прямую, параллельную данной прямой.
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Математика. 5 класс
Конспект урока
Прямая, луч, отрезок
Перечень рассматриваемых вопросов:
— понятия «прямая», «луч», «отрезок»;
— отличия прямой, луча, отрезка;
— прямая, луч, отрезок на чертежах, рисунках и моделях.
Отрезок – часть прямой, ограниченный двумя точками.
Концы отрезка – точки, ограничивающие отрезок.
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.
Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).
Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.
Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.
Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.
Через любые две точки можно провести только одну прямую.
Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.
Провести через точки А и В другую прямую, отличную от прямой b, нельзя.
Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.
Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.
Каждую из этих частей называют лучом, исходящим из точки А.
Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.
Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.
Переставлять буквы в названии луча нельзя.
Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.
Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.
В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.
Заметим, что два отрезка называются равными, если они совмещаются при наложении.
Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.
Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: добавление подписей к изображениям.
Разместите нужные подписи к изображениям.
Для выполнения задания обратитесь к теоретическому материалу урока.
№ 2. Тип задания: подстановка элементов в пропуски в тексте.
Вставьте в текст нужные слова.
Через__________ две____________ можно провести только одну _________.
Слова: любые; точки; прямую; ломаную.
Правильный ответ: через любые две точки можно провести только одну прямую.
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
Как обозначить прямую
Прямую обычно обозначают одной маленькой латинской буквой.
Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.
Задача № 1 из учебника Атанасян 7-9 класс
Решение задачи
Опишем взаимное расположение точек и прямой.
Как обозначается пересечение прямых
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).
Прямые e и f не имеют общей точки — т.е. они не пересекаются.
Взаимное расположение прямой и точек
Через одну точку (·)A можно провести сколько угодно прямых.
Через две точки (·)A и (·)B можно провести только одну прямую.
Сколько общих точек имеют две прямые
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.
Второй случай расположения прямых
Третий случай расположения прямых
Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Решение задачи
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.
Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или три.
Что такое отрезок
Отрезок — часть прямой, ограниченная двумя точками.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.