Что такое отрезок с концами данных точек
Отрезок — что это такое
Что такое отрезок? Ответ на этот вопрос кажется весьма простым, когда вы учитесь в школе. Но с возрастом школьный курс математики постепенно забывается настолько, что такие простые вещи становятся не столь очевидными.
Отрезок — что это за фигура
Не стоит недооценивать значимость геометрических понятий в человеческой жизни, так как иногда эти знания помогают решать вполне реальные задачи, а не только блистать кругозором в кругу друзей.
Отрезок — это составная часть прямой, расположенная между двумя точками.
Вы можете дать определение также исходя из структурного подхода:
Отрезок — это такая математическая фигура, которая состоит из следующих элементов:
С этими составными частями вы можете ознакомиться на слайде:
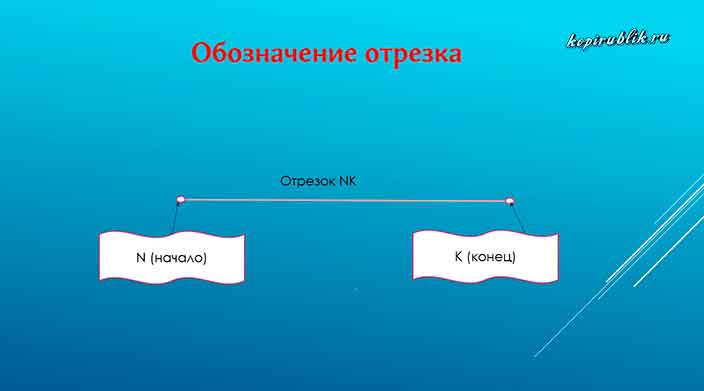
В связи с тем, что границы отрезка отмечаются точками, которые в рамках математики выделяются латинскими буквами, сама фигура описывается двумя буквами, например, NK.
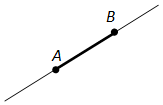
Пример визуального изображения отрезка вы видите на рисунке: точки N и K являются началом и концом.
Важная характеристика, которая присуща любому отрезку – его длина.
Основные меры измерения длины отрезков– это миллиметр, сантиметр, метр, километр.
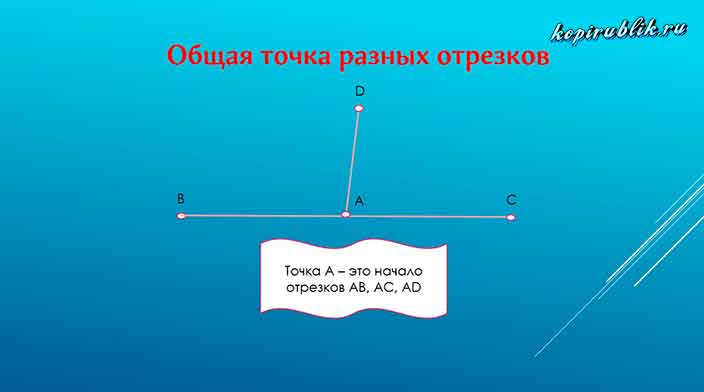
Из математической трактовки следует, что отрезок – это такая прямая, которая расположена между двумя точками не выходя за их пределы. При этом одна же точка может быть концом множества отрезков.
Такую ситуацию вы видите на рисунке: точка А является общей для всех отрезков. При этом точки B, C, D — индивидуальны для каждого из отрезков.
Сравнение отрезка с геометрическими фигурами
В математике существуют три очень похожих понятия – это отрезок, луч, прямая. Учащиеся нередко задают такой вопрос «Что такое отрезок, чем он отличается от луча и прямой?». Давайте сразу определимся с понятиями, которые позволят вам понять разницу между фигурами.
Отрезок — это часть линии, которая проходит от точки начала до точки, обозначающей конец.
Луч — составная часть прямой, которая ограничена точкой с одной стороны. С другого конца луч продлевается до бесконечности.
Прямая — это линия, не подверженная искривлениям, у которой к тому же, в отличие от отрезков, отсутствуют начало и конец.
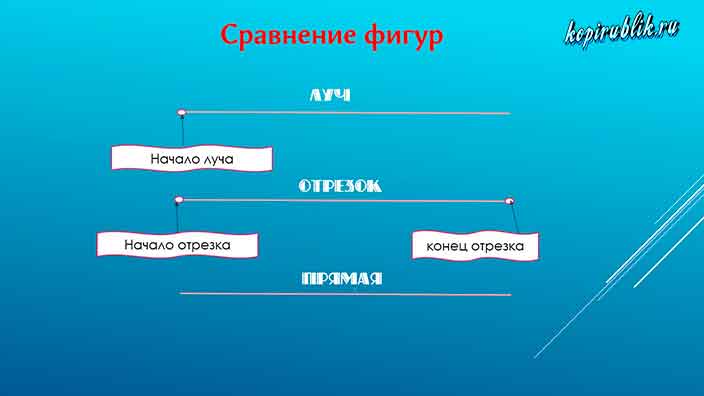
Сравнив 3 понятия, вы можете убедиться, что луч совмещает ограниченность отрезка и бесконечность прямой.
Примечательно, что прямая и луч бесконечны, поэтому вы сможете измерить длину только у отрезков.
У вас может возникнуть вопрос: «Как быстро определить, что именно перед вами — отрезок, луч или прямая?». Визуально идентифицировать геометрические фигуры можно по количеству ограничивающих их длину точек:
Направленный отрезок
В статье вы увидели базовый вид отрезка — ненаправленный. Это отрезок, у которого невозможно определить, что является его началом, а что — концом.
Существует второй вид отрезков – направленные.
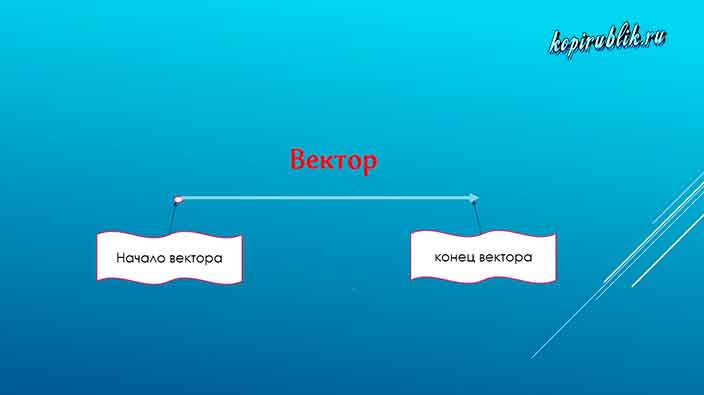
Альтернативное название этой математической фигуры — вектор.
Особенностью направленного отрезка является то, что одна из точек, ограничивающих его длину, обозначается стрелкой. Она указывает, что именно там находится конец. Соответственно часть вектора, обозначенная точкой — это его начало.
Характерной чертой вектора является то, что он может быть описан не только двумя латинскими буквами, но и одной маленькой буквой, над которой располагается стрелка.
Направленный отрезок вместо показателя длины имеет характеристику — модуль, которая измеряется величинами, измеряющими расстояние – миллиметр, сантиметр, метр, километр.
В процессе работы с отрезками возникает вопрос: «Как рассчитать модуль вектора с использованием системы координат?».
Вы определите его следующим образом:
Направленные отрезки, которые лежат на одной прямой или параллельных прямых – это коллинеарные направленные отрезки.
Направленные отрезки, расположенные на параллельных прямых – это коллинеарные направленные отрезки.
Нулевой вектор — это отрезок, у которого одна точка включает начало и его конец.
Отрезки, соединённые в ломаную линию
Ломаная линия — это совокупность соединённых между собой отрезков, в которой окончание одного отрезка совпадает с начальной точкой другого. Каждая из составных частей ломаной линии называется звеном.
Ломаная линия содержит три типа вершин — точек, из которых состоят отрезки:
Первое и последнее звенья фигуры имеют по одной точке, которую они не делят с другими звеньями, а все остальные точки являются одновременно концом одного отрезка и началом другого, поэтому количество точек ломаной линии всегда на одну больше числа составляющих её отрезков.
Сравнение отрезков
Сравнить два отрезка — это значит сделать вывод о том, одинаковы ли они, или один по размеру больше другого.
Если наложить один отрезок на другой и они совпадут — это значит, что фигуры равны.
Наложение не всегда является возможным, поэтому для сравнения размеров отрезков вы можете использовать циркуль или линейку.
Отрезок: разные значения слова
Обратите внимание, что отрезок — это не только математическое понятие, хотя наибольшее распространение получило именно в этой точной науке.
Часто слово употребляется для характеристики временного промежутка — «отрезок времени»
Так же вы можете услышать словосочетание — «отрезок пути». Эта фраза обозначает расстояние — составную часть путешествия. Суть слова «отрезок» — ограничение какого-либо понятия, которое подлежит измерению.
объясните что такое отрезок с концами в данных точках
линия, соединяющая две данные точки.
Это значит что заданы две точки на плоскости и эти точки соединены между собой прямой линией. Это и будет отрезок с концами в данных точках.
Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками. Эти точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: «отрезок AB», то подразумевают отрезок с концами в точках A и B.
Другие вопросы из категории
AP=PD BP=6.4 и Угол A=45 градусам
найдите площадь ромба если его углы относятся как 1:5 а сторона равна а
1 ТочкаFпринадлежит прямойl
2 ТочкаFне находится на прямойl.
3 ТочкаFявляется точкой прямойl.
4 ТочкаFнаходится не на прямойl.
5 ТочкаFне является точкой прямойl.
6 ТочкаFнаходится на прямойl.
Читайте также
2.Какая фигура называется углом? Объясните,что такое вершина и стороны угла.
3.Какой угол называется развернутым?
2)что такое радиус?
3)что такое отрезок?
неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 126 градусов. 4.Что такое паралельные прямые. Признаки паралельных прямых (доказать любой из признаков) 5.Что такое треугольник. Построение треугольника по стороне и двум углам 6.угол, противолежащий основанию равнобедренного треугольника, равен 50 градусов. Найди величину внешнего угла при основании. 7.Аксиома паралельных. Теоремы об углах, образованных двумя паралельными прямыми и секущей.(доказать любую теоремы)
3.Объясните, что такое луч. Как обозначают лучи. Какой луч называется биссектрисой угла.
4.Объясните, что такое отрезок. Как сравнить два отрезка. Какая точка называется серединой отрезка. Единицы измерения отрезков.
5.Какая фигура называется углом? Объясните, что такое вершина и стороны угла. Виды углов. Единицы измерения углов.
6.Соотношения между сторонами и углами треугольника.
7.Какие прямы называются перпендикулярными. Как построить перпендикулярные прямые.
8.Какой угол называется внешним углом треугольника. Свойство внешнего угла треугольника.
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии
какая фигура называется отрезком с концами в данных точках
1. Приведите примеры геометрических фигур. 2. Назовите основные геометрические фигуры на плоскости. 3. Как обозначаются точки и прямые? 4. Сформулируйте основные свойства принадлежности точек и прямых. 5. Объясните, что такое отрезок с концами в данных точках. 6. Сформулируйте основное свойство расположения точек на прямой. 7. Сформулируйте основные свойства измерения отрезков. 8. Что называется расстоянием между двумя данными точками? 9. Какими свойствами обладает разбиение плоскости на две полуплоскости? 10. Сформулируйте основное свойство расположения точек относительно прямой на плоскости. 11. Что такое полупрямая, или луч? Какие полупрямые называются дополнительными? 12. Как обозначаются полупрямые? 13. Какая фигура называется углом? 14. Как обозначается угол? 15. Какой угол называется развёрнутым? 16. Объясните, что означает выражение: «Полупрямая проходит между сторонами угла». 17. В каких единицах измеряются углы и с помощью какого инструмента? Объясните, как проводится измерение. 18. Сформулируйте основные свойства измерения углов. 19. Сформулируйте основные свойства откладывания отрезков и углов. 20. Что такое треугольник? 21. Что такое угол треугольника при данной вершине? 22. Какие отрезки называются равными? 23. Какие углы называются равными? 24. Какие треугольники называются равными? 25. Как на рисунке отмечаются у равных треугольников соответствующие стороны и углы? 26. Объясните по рисунку 23 существование треугольника, равного данному. 27. Какие прямые называются параллельными? Какой знак используется для обозначения параллельности прямых? 28. Сформулируйте основное свойство параллельных прямых. 29. Приведите пример теоремы. 30. Какие геометрические фигуры можно увидеть на фотографиях (с. 4—15)? Приведите другие примеры геометрических фигур.
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.7 / 5. Количество оценок: 3
Геометрия. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Геометрия – это наука, занимающаяся изучением геометрических фигур и отношений между ними.
Отрезок – это часть прямой, ограниченная точками, вместе с этими точками.
Концы отрезка – это точки, ограничивающие отрезок.
Теоретический материал для самостоятельного изучения.
«Геометрия – неотъемлемая часть мировой сокровищницы человеческой мысли», – однажды сказал российский математик Игорь Фёдорович Шарыгин.
С этих слов мы и начнём изучать новый раздел математики, который называется геометрия.
Геометрия – одна из древнейших наук, которая возникла из потребностей человека. Её название состоит из двух древнегреческих слов: гео – земля и метрео – измеряю, получается: «землю измеряю». Действительно, слово «геометрия» связано с измерениями, как на земельных участках, так и при строительстве зданий. Многие факты добывались опытным путем, поэтому геометрия не являлась точной наукой во времена своего зарождения.
Геометрические сведения стали доказываться только благодаря древнегреческому учёному Фалесу, который жил в VI веке до нашей эры.
Спустя некоторое время, уже в III веке до нашей эры, другой греческий учёный Евклид написал «Начала». Эта книга стала основой изучения геометрии на долгое время, а наука в честь учёного была названа евклидовой геометрией.
Сегодня геометрия – это наука, занимающаяся изучением геометрических фигур и отношений между ними.
В школе изучается два курса геометрии – планиметрия, в ней рассматриваются свойства фигур на плоскости, и стереометрия, в ней рассматриваются свойства фигур в пространстве.
В каждой науке есть свои термины, понятия, геометрия не исключение. В геометрии есть основные положения, которые принимаются в качестве исходных и носят название аксиом и основные понятия, определение которым не даётся, например, точка и прямая, но их свойства выражены в аксиомах. Это всё является фундаментом геометрии, на котором строятся другие понятия и доказываются теоремы.
Рассмотрим некоторые из аксиом.
1. Аксиомы принадлежности.
Какова бы ни была прямая, существуют точки, принадлежащие ей и не принадлежащие ей.
2. Аксиомы расположения.
Из трех точек на прямой одна и только одна лежит между двумя другими.
3. Аксиомы измерения.
Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
В целом аксиомы разделены на 5 групп, 3 из которых, частично, представлены вашему вниманию.
В 7 классе вы будете изучать планиметрию. Давайте перечислим некоторые понятия из этого раздела геометрии. Поговорим о точках, прямых, отрезках, вспомним, как они обозначаются.
Обычно прямую обозначают малой латинской буквой (например, a), а точки большими латинскими буквами, например, A.
Если на прямой отметить точки, например, A и B, то прямую в можно обозначить двумя заглавными буквами AB или BA.
Часть прямой, ограниченной точками, включая эти точки, называют отрезком. В нашем случае получаем отрезок AB или BA.
Точки, ограничивающие отрезок, называются концами отрезка. В нашем случае концами отрезка являются точки A и B.
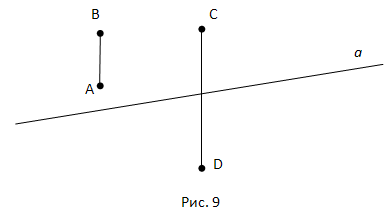
Варианты взаимного расположения точек и прямой: точки могут лежать на прямой или не лежать на ней.
Например, точки A и B лежат на прямой a, точки C и D не лежат на прямой a. При этом в записи используют следующее обозначение:
Это можно прочитать таким образом: «точка A и B принадлежат прямой a (ϵ – знак принадлежности), также точки C и D не принадлежат прямой a (перечёркнутый знак принадлежности)».
При этом через точки А и В нельзя провести прямую, не совпадающую с прямой а, из этого делаем вывод, что через любые две точки можно провести только одну прямую.
Рассмотрим, как располагаются прямые на плоскости.
Прямые могут иметь только одну общую точку, тогда говорят, что прямые пересекаются или не иметь общих точек, тогда говорят, что прямые не пересекаются.
прямые пересекаются – прямые не пересекаются
Решим задачу. Построим с помощью линейки отрезок длиннее, чем она сама. Приём, который мы будем использовать, называется провешиванием прямой.
Рассмотрим, в чём он заключается. Для этого приложим к листу бумаги линейку и отметим три точки А, В, С, при этом, точка С пусть лежит между точками А и В. Далее передвинем линейку так, чтобы её конец оказался около точки С, отметим точку D. Все построенные точки А, В, С, D лежат на одной прямой. Теперь проведём отрезок АВ, потом отрезок ВD, в результате получим отрезок АD длиннее, чем линейка.
Для построения на местности отмечают две точки, например, А и В, ставят в них шесты (вехи), третий шест ставят в точку С так, чтобы её закрывали уже ранее поставленные шесты.
Так можно прокладывать линии высоковольтных передач, трассы и т. д.
Разбор заданий тренировочного модуля.
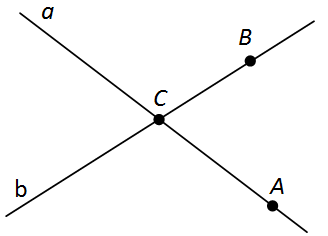
1. Сколько отрезков образуется при пересечении прямых на рисунке?
Посмотрите на рисунок. На нём изображены 4 пересекающиеся прямые, точки пересечения разбивают прямые на отрезки: прямая с разбивается на 3 отрезка АЕ, АВ, ЕВ. Аналогично все прямые разбиваются на 3 отрезка. В результате получаем, что каждая из четырёх прямых, разбивается точками пересечения на 3 отрезка, значит: 4 · 3 = 12
2. Выберите правильные варианты ответа. С чем пересекается прямая m?
Решение: при выполнении задания, нужно помнить, что прямая бесконечно продолжается в обе стороны, а отрезок ограничен точками, поэтому, если продолжить прямую m и n, то становится понятно, что они пересекутся между собой. Кроме того, прямая m пересечётся и с отрезком АВ. Следовательно, получается 2 ответа: прямая m пересекается с прямой n и отрезком АВ.
Ответ: прямая m пересекается с прямой n; прямая m пересекается с отрезком АВ.
Какая фигура называется отрезком с концами в данных точках
§1. Контрольные вопросы
Вопрос 1. Приведите примеры геометрических фигур.
Ответ. Примеры геометрических фигур: треугольник, квадрат, окружность.
Вопрос 2. Назовите основные геометрические фигуры на плоскости.
Ответ. Основными геометрическими фигурами на плоскости являются точка и прямая.
Вопрос 4. Сформулируйте основные свойства принадлежности точек и прямых.
Ответ. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Вопрос 5. Объясните, что такое отрезок с концами в данных точках.
Ответ.Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками. Эти точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: «отрезок AB», то подразумевают отрезок с концами в точках A и B.
Вопрос 6. Сформулируйте основное свойство расположения точек на прямой.
Ответ. Из трёх точек на прямой одна и только одна лежит между двумя другими.
Вопрос 7. Сформулируйте основные свойства измерения отрезков.
Ответ. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Вопрос 8. Что называется расстоянием между двумя данными точками?
Ответ. Длину отрезка AB называют расстоянием между точками A и B.
Вопрос 9. Какими свойствами обладает разбиение плоскости на две полуплоскости?
Ответ. Разбиение плоскости на две полуплоскости обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
Вопрос 10. Сформулируйте основное свойство расположения точек относительно прямой на плоскости.
Ответ. Прямая разбивает плоскость на две полуплоскости.
Многоугольники
Ломаная — это геометрическая фигура, которая состоит из точек,
соединенных отрезками. Отрезки называются звеньями ломаной,
а точки называются вершинами ломаной. Сумма длин всех
звеньев называется длиной ломаной.
Замкнутая ломаная — это ломаная, у которой конец последнего
звена совпадает с началом первого звена.
Простая ломаная — это ломаная, у которой нет пересечений.
Многоугольник — это геометрическая фигура с множеством
углов и сторон, или по другому это простая замкнутая ломаная,
у которой соседние звенья не лежат на одной прямой.
Как и у любой другой геометрической фигуры, у многоугольника
есть стороны и углы. Звенья ломаной называют сторонами
многоугольника, а вершины ломаной называют углами
многоугольника. Периметр многоугольника равен сумме
длин всех сторон многоугольника, или по другому длине ломаной.
Соседние вершины многоугольника — это два угла
многоугольника,принадлежащие одной стороне.
Диагональ многоугольника — это отрезок, соединяющий
две любые не соседних угла.
Произвольный многоугольник разделяет плоскость на две части.
Одна из частей называется внутренней областью, а другая внешней
областью многоугольника. Углы, которые находятся во внутренней
области называются внутренними, соответственно углы, которые
находятся во внешней области называются внешними.