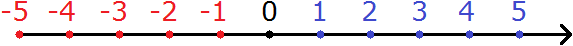Что такое отрицательные числа в математике 6 класс

Отрицательные числа

Отрицательные числа — это числа со знаком минус (−), например −1, −2, −3. Читается как: минус один, минус два, минус три.

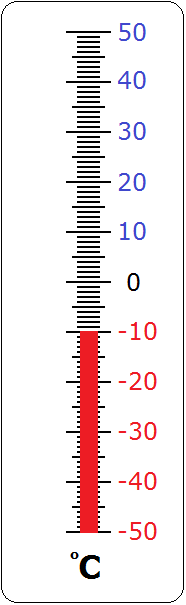
Примером применения отрицательных чисел является термометр, показывающий температуру тела, воздуха, почвы или воды. В зимнее время, когда на улице очень холодно, температура бывает отрицательной (или как говорят в народе «минусовой»).

Например, −10 градусов холода:

Обычные же числа, которые мы рассматривали ранее такие как 1, 2, 3 называют положительными. Положительные числа — это числа со знаком плюс (+).

При записи положительных чисел знак + не записывают, поэтому мы и видим привычные для нас числа 1, 2, 3. Но следует иметь ввиду, что эти положительные числа выглядят так: +1, +2, +3.

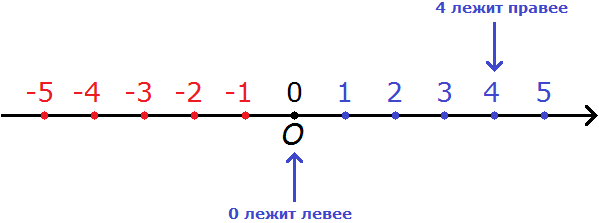
Координатная прямая

Координатная прямая это прямая линия, на которой располагаются все числа: и отрицательные и положительные. Выглядит следующим образом:

Здесь показаны только числа от −5 до 5. На самом деле координатная прямая бесконечна. На рисунке представлен лишь её небольшой фрагмент.

Числа на координатной прямой отмечают в виде точек. На рисунке жирная чёрная точка является началом отсчёта. Начало отсчёта начинается с нуля. Слева от начала отсчёта отмечают отрицательные числа, а справа — положительные.

Каждая точка на координатной прямой имеет своё имя и координату. Имя — это любая латинская буква. Координата — это число, которое показывает положение точки на этой прямой. Проще говоря, координата это то самое число, которое мы хотим отметить на координатной прямой.

Например, точка А(2) читается как «точка А с координатой 2« и будет обозначаться на координатной прямой следующим образом:

Здесь A — это имя точки, 2 — координата точки A.

Пример 2. Точка B(4) читается как «точка B с координатой 4« и будет обозначаться на координатной прямой так:

Пример 3. Точка M(−3) читается как «точка M с координатой минус три» и будет обозначаться на координатной прямой так:

Здесь M — это имя точки, −3 — координата точки M.

Точки можно обозначать любыми буквами. Но общепринято обозначать их большими латинскими буквами. Более того, начало отчёта, которое по другому называют началом координат принято обозначать большой латинской буквой O

Легко заметить, что отрицательные числа лежат левее относительно начала отсчёта, а положительные числа правее.

Сравнение отрицательных и положительных чисел

Правило 1. Любое отрицательное число меньше любого положительного числа.

Например, сравним два числа: −5 и 3. Минус пять меньше, чем три, несмотря на то, что пятёрка бросается в глаза в первую очередь, как цифра большая, чем три.

Связано это с тем, что −5 является отрицательным числом, а 3 — положительным. На координатной прямой можно увидеть, где располагаются числа −5 и 3

«Минус пять меньше, чем три»

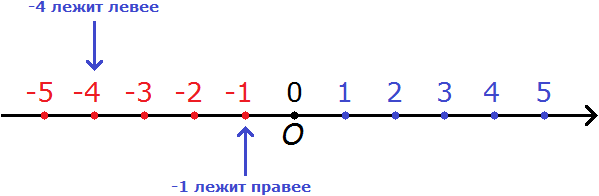
Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.

Например, сравним числа −4 и −1. Минус четыре меньше, чем минус единица.

Связано это опять же с тем, что на координатной прямой −4 располагается левее, чем −1

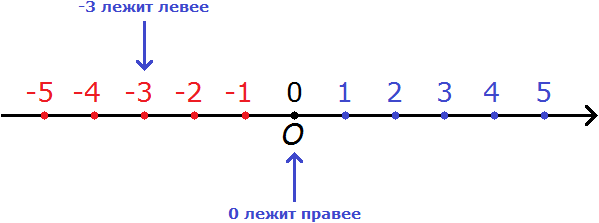
Правило 3. Ноль больше любого отрицательного числа.

Например, сравним 0 и −3. Ноль больше, чем минус три. Связано это с тем, что на координатной прямой 0 располагается правее, чем −3

Ноль больше, чем минус три

Правило 4. Ноль меньше любого положительного числа.

Например, сравним 0 и 4. Ноль меньше, чем 4. Это в принципе ясно и так. Но мы попробуем увидеть это воочию, опять же на координатной прямой:

Источник

«Отрицательные числа в изучении математики» (6 класс)

ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА.

История возникновения отрицательных чисел:

Впервые отрицательные числа появились в древнем Китае примерно 2100 лет тому назад. Там умели также складывать и вычитать положительные и отрицательные числа. Отрицательные числа трактовали как долг, а положительные как имущество. Таким же образом смотрели на эти числа и в Индии в VII столетии, но там уже были известны правила умножения и деления. Люди с некоторым недоверием относились к отрицательным числам, считая их не совсем реальными, истолкование их как имущество – долг вызвало недоумение: как можно «складывать» и «вычитать» имущество и долг.

Натуральные числа принято называть положительными целыми числами. Иногда перед положительными числами ставят знак « + ».

Два положительных или два отрицательных числа-это числа одного знака. Положительное и отрицательное число-это числа разных знаков.

С помощью знака «минус» записывается число, противоположное данному:

Если а =0, то –а = 0. Если положительные числа появились еще в древности, и стали использоваться для счета предметов, то отрицательные числа, изобретение недавнее: Отрицательные числа возникали при вычитании. Вначале они представлялись непонятными и бессмысленными, т.к наименьшим количеством было «ничто», то есть, как всегда привыкли считать это нуль. Что может быть меньше нуля?

XVII веке великий французский математик Рене Декарт предложил откладывать отрицательные числа на числовой оси влево от нуля. Отрицательные числа получили реальное истолкование. Их стали признавать наравне с положительными. Наступило полное числовое равноправие.

Из рисунка можно наблюдать, что температура может быть как выше нуля, так и ниже нуля. Со знаком «+» и со знаком «-

Любое положительное число больше нуля : 5 > 0;

Любое отрицательное число меньше нуля: — 7 0;

3.Пример применения отрицательных чисел:

Самая большая положительная величина на Земле –вершина

Самая большая отрицательная величина —

При растяжении пружины:

Правила умножения положительных и отрицательных чисел:

При умножении двух чисел с разными знаками в результате получается отрицательное число, модуль которого равен произведению модулей множителей.

При умножении двух чисел с одинаковыми знаками в результате получается положительное число, модуль которого равен произведению модулей множителей.

4.Сравнение отрицательных чисел:

>

При сравнении целых отрицательных чисел, можно представить их на координатной прямой. Точка А с координатой -7 левее, чем точка В с координатой -3,

Из двух отрицательных чисел больше то, у которых модуль меньше.

Ответ: Да, спуститься сможет. Нужно нажать на кнопку второго этажа подвала «-2»

Задание 3. Попробуйте в тексте найти положительные и отрицательные величины и сделайте выводы об их использовании в жизни.

Площадь Кунгурской Ледяной пещеры составляет 106,5 гектаров. Ее поверхность усеяна многочисленными карстовыми воронками, крупнейшие из которых достигают 50-60 метров в диаметре и 10-12 м в глубине.

В каменной нише Полярного грота скрывается массивная ледяная колонна, напоминающая застывший водопад. Ее еще описывал профессор М.Я. Киттара 165 лет назад.

Большое подземное озеро находится в гроте «Титанический» (площадь – 1300 кв.м., ширина 38 м, глубина достигает 3 м., температура воды постоянная +5 °C). В другом гроте – «Романтиков» экскурсанты могут любоваться небольшим озером с так называемым сифоном – подводным каналом, который опускается ниже уровня озера на 4-5 м.

(отрывок из книги Валентина Рапп «Путеводитель по Кунгуру и Ледяной пещере»)

1. Выгодский М.Я. Справочник по элементарной математике. – М.: Наука, 1972. – С. 130-136.

2. Едуш О.Ю. Математика. Подсказки на каждый день.

3. Лиман М.М. Школьникам о математике и математиках. – М.: Просвещение, 1981. – С. 26.

4. Новейший полный справочник школьника 5-11 классы. Том 1.– М.: Эксмо, 2014. – С. 224.

5. Рапп В.В. Путеводитель по Кунгуру и Ледяной пещере.– Пермь: Звезда, 1999. – С. 73-87.

6. История возникновения отрицательных чисел [Электронный ресурс]

7. История возникновения цифр. Применение отрицательных чисел.[Электронный ресурс]

Источник

Отрицательные числа

Отрицательное число — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.

Все отрицательные числа, и только они, меньше, чем нуль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.

Содержание

Свойства отрицательных чисел

Отрицательные числа подчиняются практически тем же правилам, что и натуральные, но имеют некоторые особенности.

Исторический очерк

Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные.

Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата. Правда, умножение и деление для отрицательных чисел тогда ещё не были определены.

Диофант в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако и он рассматривал их лишь как временные значения.

В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии.

Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).

Источник

Отрицательные числа

Всего получено оценок: 178.

Всего получено оценок: 178.

Отрицательные числа тяжело воспринимаются учениками 6 класса математики, поскольку долгое время их учат том, что все результаты вычислений, которые меньше нуля неверны. Приходится переучиваться, привыкать к новым правилам. Но на самом деле, если разобраться в отрицательных числах, ничего сложного в них нет.

Отрицательные числа

Отрицательным числом называется любое число меньше нуля. Чтобы обозначить, что число меньше нуля, перед ним ставится знак минус.

Среди отрицательных чисел так же, как и среди положительных есть дроби: обыкновенные и десятичные, целые числа, корни и так далее. Практически все подвиды чисел, которые встречаются среди положительных чисел, есть и среди отрицательных. Так же важно помнить, что число 0 не относится ни к положительным, ни к отрицательным числам.

Числовая прямая

Числовая прямая это прямая, которая имеет обозначение 0 и единичных отрезков. На числовой прямой все отрицательные числа лежат левее нуля.

Числовую прямую очень удобно использовать для сравнения отрицательных чисел. Чем ближе отрицательное число на числовой прямой к нулю, тем большим значением оно является.

Правило знаков

Умножение и деление отрицательных чисел происходит согласно правилу знаков:

Сложение отрицательных чисел

При сложении отрицательных чисел действует все то же правило знаков, только в несколько ином виде. Общая формулировка правила знаков звучит так: «Плюс на минус дает минус, минус на минус дает плюс и плюс на плюс дает плюс». Тогда если к одному отрицательному числу прибавить другое, то получится:

-а+(-в)=-а-в – то есть из отрицательного числа вычитается положительное.

Так же работает правило при примерах на вычитание отрицательных чисел:

-а-(-в)=-а+в – к отрицательному числу в итоге прибавляется положительное.

Что мы узнали?

Мы поговорили об отрицательных числах. Рассказали, как удобнее сравнивать отрицательные целые числа, а также как правильно подобные числа перемножать между собой, делить, складывать и вычитать.

Источник

Математика. 6 класс

Конспект урока

Отрицательные целые числа

Перечень рассматриваемых вопросов:

Ряд целых чисел образуют натуральные числа, целые отрицательные числа и число ноль.

Ряд целых чисел является бесконечным множеством, а часть этого ряда – все целые числа, заключённые между каким-нибудь двумя заданными целыми числами, – является конечным множеством.

Справа от числа 0 в этом ряду расположены числа, которые называются натуральными или целыми положительными.

Слева от числа 0 в этом ряду расположены числа, которые называют целыми отрицательными.

Число 0 не является ни положительным, ни отрицательным числом.

Теоретический материал для самостоятельного изучения

Отрицательные целые числа.

На рисунке термометр показывает 10 °C. Если температура понизится на 5 °C, то термометр будет показывать 5 °C. Уменьшение температуры соответствует действию вычитания:

Если температура понизится на 10 °C, то термометр будет показывать 0 °C. Уменьшение температуры соответствует действию вычитания:

Если же температура понизится на 12 °C, то термометр покажет – 2 °C (2 градуса мороза).

Но результат вычитания 10 – 12 нельзя записать с помощью натуральных чисел и нуля, хотя он имеет реальный смысл.

Проиллюстрируем вычитание на ряде целых неотрицательных чисел:

Отсчитать в ряду натуральных чисел и нуля от числа 10 влево 12 чисел нельзя.

Расширим ряд неотрицательных целых чисел.

Влево от нуля запишем, справа налево по порядку, все натуральные числа, добавляя к каждому из них знак «–», показывающий, что это число стоит слева от нуля.

…, – 6, – 5, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …

Записи – 1, – 2, – 3, … читают «минус 1», «минус 2», «минус 3» и т. д.

Полученный ряд чисел называется рядом целых чисел.

…, – 6, – 5, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …

Точки слева и справа в этой записи означают, что ряд можно продолжать неограниченно вправо и влево.

Справа от числа 0 в этом ряду расположены числа, которые называются натуральными или целыми положительными.

Слева от числа 0 в этом ряду расположены числа, которые называются целыми отрицательными.

Число 0 не является ни положительным, ни отрицательным числом. Оно разделяет положительные и отрицательные числа.

…, – 6, – 5, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …

Ряд целых чисел образуют натуральные числа, целые отрицательные числа и число нуль.

Ряд целых чисел является бесконечным множеством, а часть этого ряда – все целые числа, заключённые между какими-нибудь двумя заданными целыми числами, – является конечным множеством.

– 2, – 1, 0, 1, 2, 3, 4 – конечное множество.

Стрекоза может перелететь с любого целого числа только на соседнее целое число. Какое наименьшее количество полётов ей понадобится совершить, чтобы с числа – 5 попасть на число 8?

Стрекоза может перелетать только на соседнее целое число, значит от – 5 до 8 нужно:

Разбор заданий тренировочного модуля

Тип 1. Единичный выбор.

Утром температура воздуха была + 9˚ и к 12:00 понизилась на 10˚. Какой стала температура воздуха?

Варианты ответов: – 19, + 19, – 1, – 1

Тип 2. Ввод с клавиатуры пропущенных элементов в тексте.

Сколько целых чисел расположено правее числа – 8, но левее числа 2?

…, – 8, __, __, __, __, __, __, __, __, __, 2, …

Распишем числа, которые располагаются в ряду целых чисел, между заданными числами:

…, – 8, – 7, – 6, – 5, – 4, – 3, – 2, – 1, 0, 1, 2, … Посчитаем их количество.

Источник