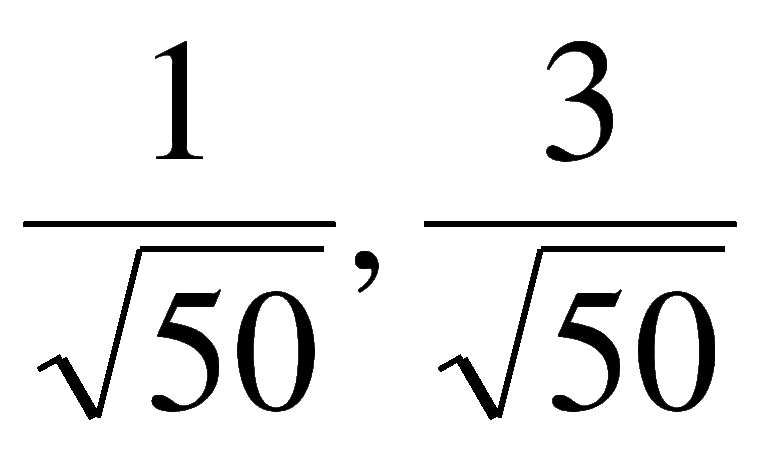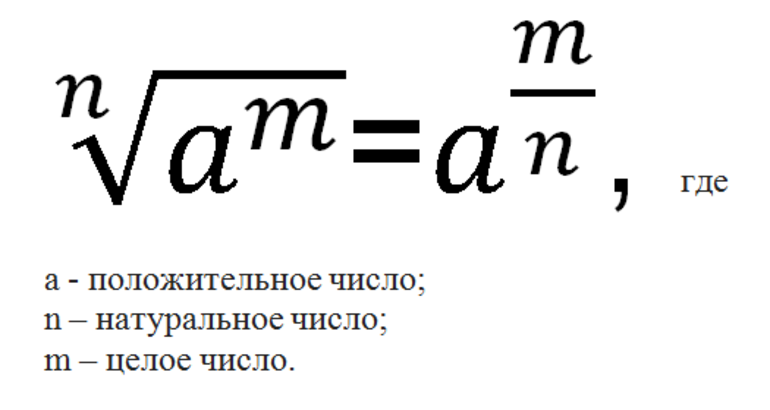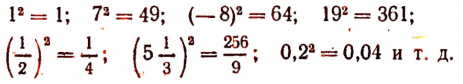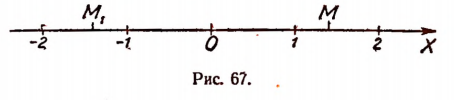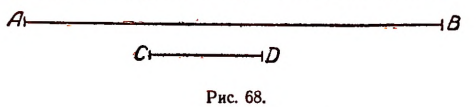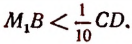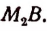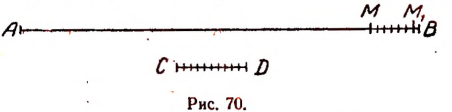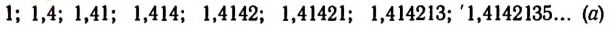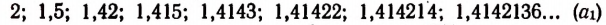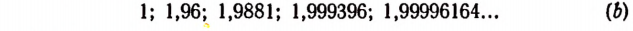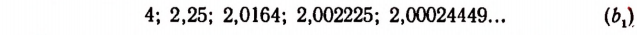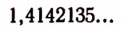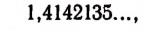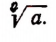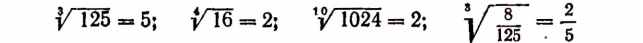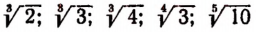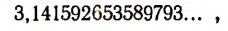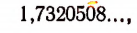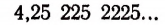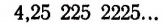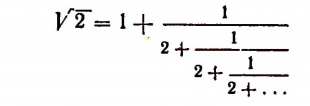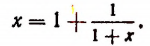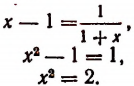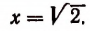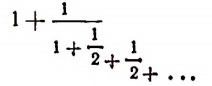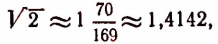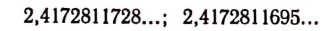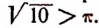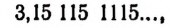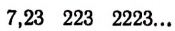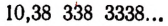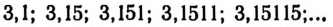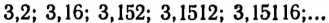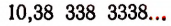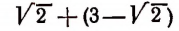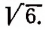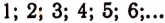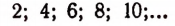Что такое отрицательные иррациональные числа в математике

История открытия

Одни учёные считают, что иррациональные числа были открыты Пифагором. Другие полагают, что существование таких величин было выявлено пифагорейцами в V веке до нашей эры. Третьи выдвигают версию, что открытие принадлежит древним учёным Азии.

Несмотря на то что возникновение нового типа чисел связывают с именем Пифагора, сам великий учёный этих величин не признавал. Математик основывал свои труды на рациональности значений, а потому их иные виды были неприменимы к его теориям. Из-за огромного авторитета учёного иррациональные значения стали использоваться в науке только после его смерти.

Аристотель доказал иррациональность квадратного корня из 2. Теодор из Кирены привёл подобные доказательства в отношении корня из 3, 5 и так далее. Есть версия, что даже термины для соответствующей теории ввёл этот математик. Его ученик Теэтет на основании указанных данных создал общее учение об иррациональности. Полная теория иррациональных количественных значений Эвклид изложил в пятой книге «Начал».

Понятие и характеристика

Огромным прорывом в математической науке стали числа, которые называются иррациональными. Какие-либо ограничения, связанные с целыми величинами или обыкновенными дробями, были сняты. Люди получили возможность открывать и даже изобретать новые количественные значения.

Иррациональным считается вещественное число, не являющееся рациональным. Оно не может быть представлено в виде арифметической дроби n/m, где числитель и знаменатель являются целыми величинами, а n не равно 0. Также подобные значения невозможно точно выразить целой величиной. Это значит, что иррациональные числа всегда выглядят, как бесконечные непериодические десятичные дроби. Для их обозначения применяют радикалы или специальные буквы, например, е, π. Множество чисел обозначается заглавной буквой в полужирном начертании без заливки.

В геометрии оно представляется в качестве отрезка, длина которого несоизмерима с единичной. Об этой несоизмеримости упоминали и древние математики. Они установили, что диагональ квадрата не имеет общей меры с его стороной, что равносильно иррациональности корня из 2.

Не всякая величина из множества значений, не относящихся к рациональным, так известна, как число π. В школьной программе его часто определяют, как 3,14, но истинный показатель π значительно ближе к 3. Следует отметить, что даже известная длинная десятичная дробь является лишь приближённым вариантом, поскольку указанное число нельзя точно установить. Дробь, которую используют для этого, бесконечна, а цифры в ней распределяются без какой-либо закономерности.

Самыми известными примерами таких иррациональных чисел являются:

Математиками составлены специальные таблицы величин, не являющихся рациональными. Но так как множество бесконечно, определить тип значения по данным таблицам довольно сложно.

Зачастую понять, что число иррационально, можно по его соответствию одному из перечисленных признаков:

Но в ряде случаев установить иррациональность значения возможно только посредством доказательства. К примеру, школьникам часто дают задание доказать, что число log3 4 не относится к рациональным.

Отличительные качества

Значения, которые нельзя выразить дробью, существенно отличаются от других чисел. К их уникальным свойствам относятся следующие:

Виды преобразования выражений

Иррациональные выражения содержат операцию извлечения корня. Это особые записи, состоящие из радикалов и знаков алгебраических действий.

Во время преобразования таких выражений нельзя допускать сужения области допустимых значений. С ними разрешается проводить любые из основных тождественных преобразований:

В основе подобного упрощения выражений лежат действия, общие для всех количественных значений. Поэтому в процессе преобразования этих записей необходимо сохранять установленный порядок выполнения действий.

Замена исходной записи

Подкоренное выражение можно заменить тождественно равным, то есть математической записью, значение которой будет равно исходному. Следует учитывать, что равенство должно соблюдаться при любых допустимых значениях переменных, которые входят в состав обоих выражений.

Это утверждение основывается на единственности корня из числа. Иными словами, нет значения, которое, отличаясь от исходной величины, сохраняло бы равенство с нею.

Использование свойств корней

Для упрощения сложных выражений часто применяются свойства корней, к примеру, перемножение их степеней. Делать это необходимо в соответствии со специальными формулами.

Особое внимание при работе следует обращать на отрицательные числа и выражения с переменными. В ряде случаев для применения формул такие значения сначала придётся привести к тождественно равным, которые подойдут для дальнейшего использования свойств корней.

Внесение множителя под знак корня — это преобразование произведения, в котором лишь один из множителей находится под знаком радикала со степенью, выраженной натуральным числом. После замены выражения под корнем будут находиться все множители, составляющие произведение, но оно останется равным исходному.

Обратным изменением является вынесение множителя из-под радикала. Его используют в случаях, когда степень корня равна степени множителя под радикалом. В таких ситуациях указанный множитель можно извлечь и тем самым упростить выражение.

Изменение дробей

Иррациональные математические записи могут содержать дроби с радикалами в делимом или делителе. С ними разрешается проводить любые действия, относящиеся к основным преобразованиям дробных чисел:

Избавление от иррациональности в знаменателе

Освобождение от иррациональности в знаменателе представляет собой преобразование дроби путём её замены на тождественно равную с делителем, не содержащим корней и степеней. Для этого необходимо последовательно провести два действия:

Переход к степеням

Переход от радикалов к степеням осуществляется на основе равенства, давшего определение степени, которая имеет рациональный показатель. При этом используется следующая формула:

Если же величина под радикалом отрицательная или там находится выражение с переменными, то перед использованием формулы подкоренное значение необходимо преобразовать. Для этого следует применять свойства степеней.

Математические действия

Иррациональные выражения записывают друг за другом с сохранением знаков и лишь после этого складывают или вычитают. Иногда их преобразуют в подобные, то есть имеющие одинаковые подкоренные значения, а затем проводят арифметические действия.

Чтобы найти произведение выражений с одинаковыми радикалами, умножают значения, находящиеся под знаком корня. Полученный результат вносится под корень изначальных выражений.

При делении степени корней делимого и делителя также должны быть равны. Если это условие соблюдено, то первое выражение делится на второе, после чего итог действия записывается под исходный знак радикала.

Правила сравнения

Иногда для решения математических задач необходимо провести сравнение иррациональных значений. При этом необходимо руководствоваться следующими правилами:

Для возведения иррациональной величины в степень необходимо возвести в неё значение под радикалом. Если величина корня равна степени, то в итоге число или выражение выносится из-под корня неизменным, поскольку возникают взаимно сокращающиеся действия.

Если иррациональное выражение находится под корнем, то для его извлечения показатели радикалов умножают. Этот метод позволяет упрощать извлечение корней четвёртой, шестой, восьмой, девятой степени.

Иррациональные числа можно узнать по специальным буквам, используемым для их обозначения, или по написанию в виде десятичных дробей, не имеющих окончания. Выражения этого типа легко отличить по наличию радикала. С подобными значениями проводят те же действия, что и с другими вещественными числами. Их можно умножить, сложить, сравнить и так далее.

Источник

Базовые сведения об иррациональных числах

Дроби достаточно хороши для любой практической задачи на деление, и некоторое время древние греки были убеждены, что дроби описывают все во Вселенной.
Затем один из них разобрал следствия теоремы Пифагора и задался вопросом о том, как диагональ квадрата относится к его стороне.
Из ответа на этот вопрос следовало, что некоторые задачи решить с помощью дробей невозможно.
Так родились иррациональные числа. Вместе рациональные и иррациональные числа образуют множество действительных чисел.

Прежде чем детально объяснить читателю какие числа являются иррациональными и каковы их свойства, потребуется напомнить некоторые базовые понятия.

Базовые понятия

Натуральными (от латинского “ naturalis ” – “естественный”) называют числа, возникшие из естественной нумерации предметов при счёте – например такие как 1, 2, 3 и так далее. Их последовательность, расположенная в порядке возрастания, образует так называемый натуральный ряд. Существует два конкурентных подхода к определению ряда натуральных чисел: в отечественной математической литературе он традиционно начинается с единицы, в зарубежной – с нуля.

Целыми называют числа, образованные расширением множества натуральных чисел посредством добавления отрицательных чисел и нуля: за счёт такого объединения в общем случае из меньшего числа можно вычесть большее, что уравнивает операции вычитания и сложения, образуя “кольцо целых чисел“.

Рациональными (от латинского “ ratio ” – “дробь”, “отношение”, часто в данном контексте неправильно толкуемое в популярных статьях как определение “разумный” либо аналогичное) числами называют числа вида m/n, где числитель m представлен целым числом, а знаменатель n – натуральным. Иначе говоря, рациональными являются те числа, которые возможно точно представить в виде обыкновенной дроби.

Пояснение-напоминание о дробях

Прежде чем дать определение какие числа называются иррациональными, потребуется напомнить читателю некоторые сведения о дробях и формах их представления. Общепринятыми для записи дробей являются два формата: обыкновенные (вида m/n) и десятичные (вида 0,12345). В случае десятичных дробей дополнительно вводится понятие периодичности: например, дробь 1/7 в десятичном виде может быть представлена как 0,(142857), где в скобках заключён бесконечно повторяющийся фрагмент – так называемый период дроби.

Определение иррациональных чисел

Итак, иррациональные числа – это такие числа, которые невозможно точно отобразить посредством обыкновенной дроби, но возможно представить в виде бесконечной непериодической десятичной дроби. С точки зрения иррациональности в математике, множество иррациональных чисел является разностью между множеством чисел вещественных и множеством чисел рациональных.

С понятием иррационального числа близко столкнулись ещё древние учёные: так, индийский математик Манава обнаружил, что диагональ условного квадрата с единичной стороной имеет размерность √2, что невозможно выразить явно доступными в то время средствами. Другим известным примером является так называемая “постоянная Архимеда” – число Пи (отношение диаметра окружности к её длине). Важно понимать, что для инженерных расчётов возможно использование его рациональных приближений различной степени точности в виде дробей 22⁄7, 179⁄57, 223⁄71 и так далее, но ни одна из этих дробей по определению не является точным представлением числа Пи.

Некоторые примеры рациональных и иррациональных чисел:

рациональные – дроби типа 1/3 или 0,(142857) и им подобные;

иррациональные – квадратные корни √2, √3 и √5, основание натуральных логарифмов e, число Пи и так далее.

Легко заметить, что отрицательные иррациональные числа отличаются от положительных лишь знаком и располагаются на числовой прямой симметрично относительно начала координат (нуля).

Общие признаки рациональных выражений/чисел

Вопрос “как определить иррациональные числа” не имеет однозначного ответа: если имеется некое математическое выражение для числа, то для выяснения его рациональности/иррациональности потребуется произвести детальное исследование. Резко сократить время на поиск требуемого доказательства возможно, если пойти от противного: убрать из рассмотрения числа, не являющиеся иррациональными. По определению, к ним не могут принадлежать:

все целые, натуральные и рациональные числа;

обыкновенные дроби и смешанные числа;

бесконечные и конечные периодические десятичные дроби.

Результат математических операций (сложение, умножение, вычитание и деление) над рациональными числами также не является иррациональным числом. Если в исследуемое выражение входит единственное иррациональное число, то результат также будет иррациональным – однако для случая двух и более вхождений это, вообще говоря, неверно.

Некоторые признаки иррациональных выражений/чисел

Вот некоторые общеупотребительные признаки иррациональности исследуемого выражения/числа:

корень k-ой степени из целого числа будет рациональным только тогда, когда подкоренное выражение является k-ой степенью иного целого числа;

в случае использования обычных логарифмов иррациональность выражения непременно требует доказательства (здесь удобнее всего пользоваться методом “от противного”);

поскольку основанием натуральных логарифмов является иррациональное число e, то натуральный логарифм любого положительного числа также будет иррациональным;

иррациональное число e в любой рациональной (но отличной от нуля!) степени даёт иррациональный результат;

число Пи в любой целой и отличной от нуля степени даёт иррациональный результат;

все основные тригонометрические функции (такие как cos (a), sin (a), tg(a) и ctg (a)) при использовании отличного от нуля рационального аргумента в качестве результата дают иррациональное число.

Интересные факты об иррациональных числах

Как известно Пифагор возвёл числа во главе культа, основным постулатом которого являлось то, что всё во вселенной являлось целочисленном выражении. Его учение собрало последователей в тайное сообщество математиков – пифагорейцев, которое возглавил сам Пифагор. Один из последователей Пифагора – Философ-пифагореец Гиппас высчитал, что в случае, если стороны треугольника равны одной мере длины, то протяженность гипотенузы составит корень из числа 2 ( v2). Ответ полученный при извлечении квадратного корня является целым числом, а значит не имеет точного целочисленного значения, т.е. является ни чем иным как иррациональным числом. Интересный факт в том, что Пифагор, узнав что Гипас ставит под сомнение его учения о целочисленности природы, хоть и не специально, пригласил его на рыбалку, а на берег возвратился уже в одиночку… Гипаса после этой рыбалки никто уже больше не видел.

Выводы

Все вышеперечисленные признаки являются плодом строгого математического доказательства, а иные конкретные частные случаи требуют дополнительного исследования – то есть не существует всеобщих, однозначных и очевидных признаков иррациональности. Например, возведение в иррациональную степень иррационального числа совершенно не обязательно сопровождается получением иррационального результата. Кроме того, имеются частные случаи, когда вычитание, сложение, деление и умножение иррациональных чисел в итоге даёт рациональный результат. В общем случае для доказательства рациональности/иррациональности применяется специальная доказательная база, строящаяся на теории алгебраических и трансцендентных чисел. Особо отметим, что для целого ряда случаев рациональность либо иррациональность выражения/результата не доказана до сих пор.

Источник

Иррациональные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение иррациональных чисел

Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:

Оно может быть выражено в форме бесконечной непериодической десятичной дроби.

Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.

Примеры иррациональных чисел:

Множество иррациональных чисел договорились обозначать латинской буквой I.

Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.

Свойства иррациональных чисел

Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.

Свойства иррациональных чисел:

Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.

Определение рациональных чисел

А теперь наоборот: рассмотрим противоположное заданной теме определение.

Рациональное число — это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.

Рациональные числа — это те, которые можно представить в виде:

где числитель m — целое число, а знаменатель n — натуральное число.

Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Множество рациональных чисел принято обозначать латинской буквой Q.

Примеры рациональных чисел:

У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.

Основные свойства действий с рациональными числами

Источник

Иррациональные числа в математике и их свойства с примерами решения и образцами выполнения

На первый взгляд может показаться, что никаких других чисел, кроме рациональных, и быть не может. В действительности же это не так. Мы увидим, что, кроме рациональных чисел, существуют и другие.

Станем исходить из того, что нам известны лишь рациональные числа и никакие другие. Тогда действие возведения в квадрат иад этими числами окажется выполнимым всегда.

Между тем действие извлечения квадратного корня выполнимо уже далеко не всегда.

Например, действие извлечения квадратного корня из двух окажется невыполнимым, так как во множестве рациональных чисел нет такого числа, квадрат которого был бы равен двум (см. стр. 244).

Таким образом, чтобы сделать возможным выполнение действия извлечения арифметического квадратного корня, во всех случаях снова требуется прибегнуть к дальнейшему расширению нашего понятия о числе.

Здесь мы снова видим, что для выполнения прямого действия (возведения в квадрат) не требовалось расширять рациональную числовую область, а для безотказного выполнения обратного действия (извлечения квадратного корня) такое расширение уже становится необходимым.

К расширению области рациональных чисел нас приводит и рассмотрение вопроса об отношении несоизмеримых отрезков (см. стр. 247).

Действительно, оставаясь в области рациональных чисел, мы не можем выразить точно отношение несоизмеримых отрезков, а следовательно, и длину отрезка, несоизмеримого с единицей длины (см. стр. 248).

Таким образом, к расширению рациональной числовой области приводят нас потребности не только алгебры, но и геометрии.

Существование на числовой оси точек, не являющихся рациональными

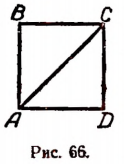
Было доказано, что диагональ и сторона квадрата несоизмеримы (см. стр. 246). Отсюда вытекает следующее: если длину стороны квадрата принять за единицу, то не будет существовать никакого рационального числа, которое выражало бы точно длину диагонали.

Пусть ABCD (рис. 66) есть квадрат, сторона которого принята за единицу длины.

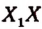
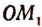
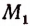
Отложим на числовой оси (рис. 67) отрезки ОМ и равные диагонали АС. Тогда точки М и не будут рациональными («черными») точками числовой оси, а следовательно, будут точками, которые мы назвали образно «красными».

Но так как отрезков, несоизмеримых с единицей; длины, существует бесконечное множество то и точек на числовой оси, не являющихся рациональными, также существует бесконечное множество.

Выше мы назвали образно все рациональные точки числовой оси «черными», а все остальные «красными». Отсюда следует, что «черные» и «красные» точки заполняют собой всю числовую ось сплошь. Иначе говоря, на числовой оси, кроме рациональных («черных») и нерациональных («красных») точек, никаких других точек нет.

В § 5, гл. XVII было доказано, что между двумя любыми различными рациональными («черными») точками существует бесконечное множество других рациональных («черных») точек. В связи с этим примем к сведению без доказательства следующее: на любом сколь угодно малом отрезке числовой, оси, где бы он ни был расположен, имеется бесконечное множество рациональных („черных») и бесконечное множество „красных» точек.

При этом оказывается, что бесконечное множество нерациональных (т. е. «красных») точек числовой оси существенно «богаче» множества ее рациональных (т. е. «черных») точек. Это же самое в точных терминах можно сформулировать так: множество нерациональных (т. е. «красных») точек числовой оси имеет мощность (см. §6 этой же главы) более высокую, чем мощность множества рациональных (т. е. «черных») точек.

Выражаясь образно, можно сказать, что числовая ось настолько сильно насыщена «красными» (т. е. нерациональными) точками, что вся она, по нашей условной терминологии, представлялась бы нам как бы сплошь красной.

Понятие об иррациональном числе

1. Мы убедились в том, что одних рациональных чисел недостаточно для потребностей алгебры и геометрии.

Мы видели, что нет такого рационального числа, которое равнялось бы точно . (Аналогично можно было бы убедиться, что нет таких рациональных чисел, которые равнялись бы точно, например, и многим другим квадратным корням.) Мы знаем еще и то, что существуют отрезки, точное отношение которых не выражается никаким рациональным числом (см. стр. 247). Мы также знаем, что на числовой оси существуют такие точки, точные расстояния которых от начальной точки числовой оси не выражаются никакими рациональными числами (см. стр. 254). Значит, для изображения этих величин необходимы какие-то новые числа.

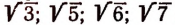
Как же составить представление об этих новых числах.

Во-первых, заметим, что такими новыми числами никак не могут быть ни конечные десятичные дроби, ни бесконечные периодические десятичные дроби, так как те и другие являются числами рациональными (см. стр. 251).

Во-вторых, заметим, что никакая бесконечная непериодическая дробь не может изображать собой рациональное число, так как всякое рациональное число (как известно из арифметики), будучи изображенным в форме бесконечной дроби, дает дробь обязательно периодическую.

Чтобы составить себе представление об этих новых числах, рассмотрим еще раз вопрос об измерении отрезка, несоизмеримого с единицей длины, и вопрос о квадратном корне из двух.

Пусть отрезки АВ и CD (рис. 68)

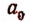
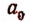
Первый шаг. Примем отрезок CD за единицу измерения и станем откладывать его последовательно на отрезке АВ. Пусть отрезок CD отложился раз и получился остаток MB, меньший CD. (На рис. 69 = 5.) Эту операцию назовем первым шагом.

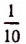
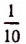
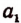
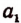
Второй шаг. Разделим отрезок CD на десять равных частей и будем откладывать часть CD на остатке MB. Пусть часть CD отложилась на MB раз (на рис. 70 = 6).

Тогда обязательно получится второй остаток

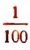
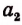
Третий шаг. На втором остатке откладываем часть CD. Получим целое число и третий остаток

Этот процесс мы продолжаем дальше, делая четвертый, пятый и дальнейшие шаги.

В силу несоизмеримости отрезков АВ и CD этот процесс теоретически никогда не кончится и длина АВ выразится бесконечной десятичной дробью. Эта бесконечная десятичная дробь не будет периодической, так как в таком случае отрезки АВ и CD оказались бы соизмеримыми, тогда как по условию они несоизмеримы.

Вот эта бесконечная непериодическая десятичная дробь и будет примером нового числа, не являющегося рациональным и называемого иррациональным. Этим числом и будет выражаться длина отрезка АВ.

Определение:

Иррациональным числом называется бесконечная непериодическая десятичная (положительная или отрицательная) дробь.

Например, бесконечная непериодическая дробь

8,121121112…

есть вполне определенное иррациональное число.

Ниже будет показано, что математическое выражение, например есть также определенное иррациональное число.

Мы уже умеем находить приближенные значения с любой сколь угодно высокой степенью точности, т. е. мы можем находить сколько угодно десятичных знаков, идущих после запятой в десятичной дроби, которая изображает приближенное значение .

При этом нам ясно, что процесс извлечения никогда не может закончиться. Если бы этот процесс мог закончиться, то был бы равен некоторой дроби , что невозможно.

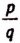
Нам также ясно, что в результате бесконечного процесса извлечения не может получиться периодическая бесконечная дробь. Если бы получилась периодическая бесконечная дробь, то это означало бы опять, что равен некоторой дроби , что невозможно. (Ведь периодическая бесконечная дробь есть число рациональное.)

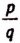
Бесконечный ряд чисел

представляет собой приближенные значения с недостатком, с точностью до и т. д.

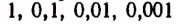
Бесконечный же ряд чисел

представляет собой приближенные значения с избытком, с точностью до и т. д.

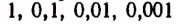
Квадратами чисел ряда (а) будут

Квадратами чисел ряда (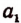) будут

Числа, записанные в рядах (b) и 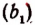, становятся тем ближе к числу 2, чем больше десятичных знаков мы берем.

Ряд (а) обладает той особенностью, что раз полученный десятичный знак навсегда сохраняется при продолжении процесса.

Это, естественно, приводит к мысли принять за бесконечную десятичную дробь

Но эта бесконечная дробь не может оказаться периодической, как это уже было доказано выше.

Итак, квадратный корень из двух изображается бесконечной непериодической десятичной дробью. Следовательно, есть число иррациональное.

Написать бесконечную непериодическую десятичную дробь, разумеется, нельзя. Мы, однако, считаем ее определенной, если имеется то или иное правило, позволяющее написать любой его десятичный знак, как бы далеко ни стоял этот знак в последовательности десятичных знаков.

Например, тысячный знак в бесконечной десятичной дроби

изображающей иррациональное число имеет вполне определенную величину, несмотря на то, что его едва ли кто знает. Впрочем, при помощи современных электронных цифровых вычислительных машин найти этот тысячный знак можно довольно быстро.

Аналогично тому, как мы доказали, что есть число иррациональное, можно доказать, что числа и т. д. также являются иррациональными.

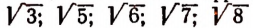
Чтобы показать существование других иррациональных чисел, введем понятие арифметического корня n-й степени.

Определение:

Арифметическим корнем n-й степени из положительного числа а называется такое новое положительное число, п-я степень которого равна а.

Корень n-й степени из а обозначается символом

Примеры:

Корни 3-й степени называют кубическими корнями. Например, 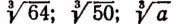суть кубические корни.

Примем к сведению без доказательства, что, например,

и им подобные представляют собой числа иррациональные.

Но ошибочно было бы думать, что иррациональные числа порождаются только корнями. Наоборот, существует много других источников, порождающих иррациональные числа. Например, мы видели, что длина всякого отрезка, несоизмеримого с единицей длины, есть число иррациональное, независимо от того, может или не может эта длина выражаться точно с помощью одного или нескольких корней.

Доказано, что отношение длины окружности к своему диаметру есть число иррациональное. Доказано, кроме того, что это иррациональное число не может быть точно представлено с помощью одного или нескольких корней.

Отношение длины окружности к своему диаметру принято обозначать греческой буквой 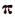(«пи»).

Иррациональность числа 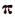впервые была доказана немецким математиком Ламбертом в 1766 году.

Число 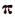изображается бесконечной непериодической дробью

первые 15 десятичных знаков которой здесь выписаны.

Число 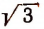изображается бесконечной непериодической дробью

первые 7 десятичных знаков которой здесь выписаны.

Мы уже знаем, что любая бесконечная непериодическая десятичная дробь представляет собой число иррациональное.

Теперь может возникнуть вопрос о том, как же понимать смысл самой бесконечной непериодической десятичной дроби.

Возьмем какую-нибудь бесконечную непериодическую десятичную дробь, например 4,25 225 2225… Составим две последовательности чисел.

Первая последовательность: 4,2; 4,25; 4,252; 4,2522; 4,25225…

Вторая последовательность: 4,3; 4,26; 4,253; 4,2523, 4,25226…

Доказано (доказательства мы здесь не приводим), что этими двумя бесконечными последовательностями определяется единственное число, которое больше каждого числа первой последовательности и меньше каждого числа второй последовательности. Это единственное число мы и понимаем под символом

Таким образом, конкретное представление об иррациональном числе

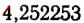
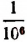
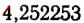
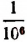
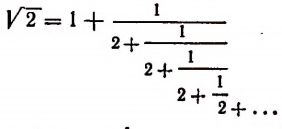
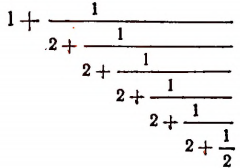
мы можем себе составить путем рассмотрения указанных выше двух бесконечных последовательностей. Эти две бесконечные последовательности дают возможность находить приближенные значения определяемого ими иррационального числа с любой точностью— с недостатком и с избытком. Например, число есть приближенное значение с недостатком с точностью до . Число же есть приближенное значение с избытком с точностью до .

Мы уже убедились в том, что всякая бесконечная десятичная непериодическая дробь является числом иррациональным. Однако существуют и другие бесконечные процессы, определяющие собой то или иное иррациональное число. Например, бесконечный процесс

определяет собой иррациональные числа , так что

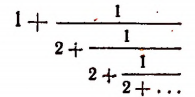
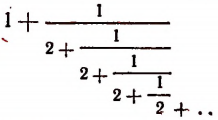
Пояснения к формуле

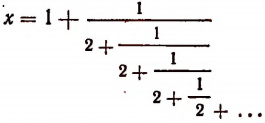
представляет собой некоторый, идущий по определенному закону, бесконечный процесс. Если допустить, что этот бесконечный процесс определяет собой некоторое число то получим

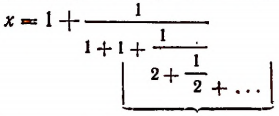
Перепишем эту формулу в следующем виде:

Выражение в предыдущей формуле, отмеченное одной фигурной скобкой, представляет тот же самый бесконечный процесс, которым (как мы допустили) определяется число х. Поэтому получим, что

Из этого уравнения следует, что

Но так как х — число положительное, то

Итак, доказано следующее. Если допустить, что бесконечным процессом

определяется некоторое число, то этим числом будет как раз иррациональное число .

Примем к сведению без доказательства, что, беря все большее и большее число звеньев этого бесконечного процесса, мы можем получать рациональные приближения иррационального числа 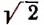все с большей и большей точностью.

Например, значение выражения

равно 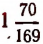. Отсюда

что как раз и представляет приближенное значение 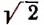с недостатком с точностью до 0,0001.

Сравнение иррациональных чисел

Два иррациональных числа называются равными, если их изображения с помощью бесконечных непериодических десятичных дробей одинаковы (тождественны).

Из двух положительных иррациональных чисел больше то, у которого целая часть больше. Если же целые части равны, то большим будет то, у которого больше первый десятичный знак после запятой. Если же и первые десятичные знаки одинаковы, то большим будет то, у которого больше второй десятичный знак и т. д.

Например, сравним следующие иррациональные числа:

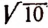
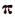
Здесь одинаковы целые части; первые семь десятичных знаков во втором числе такие же, как и в первом. Восьмой десятичный знак первого числа больше восьмого десятичного знака второго числа. Поэтому первое иррациональное число больше второго. Выписав достаточное число десятичных знаков бесконечных непериодических десятичных дробей изображающих иррациональные числа и , убедитесь, что

Сложение и умножение иррациональных чисел

Поясним, что такое сумма двух иррациональных чисел. Пусть иррациональное число а изображается следующей бесконечной непериодической десятичной дробью

а иррациональное число b — дробью

Тогда сумма а + b изобразится дробью

Эта дробь бесконечная, непериодическая, десятичная; значит, она изображает собой определенное иррациональное число.

Напишем последовательности чисел, изображающих приближенные значения числа а:

с недостатком:
с избытком:

Сделаем то же самое и для числа b:

Составим еще две следующие последовательности:

В последовательности (I) идут суммы соответствующих приближенных значений чисел a и b с недостатком, ав(II)с избытком.

Под суммой а + b подразумевается такое число, которое больше каждого члена бесконечной последовательности (I) и меньше каждого члена бесконечной последовательности (II).

Таким числом как раз будет дробь

Определение:

Суммой двух положительных иррациональных чисел называется число, которое больше суммы любых их приближенных значений с недостатком, но меньше суммы любых их приближенных значений с избытком. Такое число, как это доказано в строгой теории иррациональных чисел, всегда существует и притом только одно.

Сумма двух иррациональных чисел, вообще говоря, будет числом иррациональным, но может оказаться и рациональным.

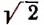
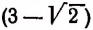
Например, числа и оба иррациональные, между тем как их сумма

есть рациональное число 3.

Определение:

Произведением двух положительных иррациональных чисел называется число, которое больше произведений любых их приближенных значений с недостатком, но меньше произведений любых их приближенных значений с избытком.

Такое число также всегда существует и притом только одно.

Произведение двух иррациональных чисел, вообще говоря, будет числом иррациональным, но может оказаться и рациональным.

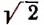
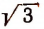
Например, произведение иррациональных чисел и будет иррациональным числом, равным

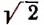
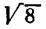
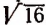
Произведение же иррациональных чисел и будет равно , т. е. рациональному числу 4.

По аналогии с приведенными рассуждениями читатель сможет сам составить определения сложения и умножения двух чисел для того случая, когда одно из них рациональное, а другое иррациональное.

Подобно этому определяется вычитание и деление иррациональных чисел.

Понятие действительного числа

Определение:

Все рациональные и иррациональные числа, как положительные, так и отрицательные, называются действительными, или вещественными, числами.

Примем к сведению без доказательства, что особенности нуля и единицы (см. стр. 41), а также переместительный и сочетательный законы сложения и переместительный сочетательный и распределительный законы умножения (см. стр. 32 и 39) остаются в силе для всех действительных чисел (рациональных и иррациональных).

Примеры для закрепления терминологии

Слово «рациональный» происходит от латинского слова «rationalis», что означает — «разумный», «обоснованный».

Слово «иррациональный» происходит также от латинского слова «irratlonalis», что означает — «неразумный», «необоснованный».

Можно было бы подумать, что числа, несоизмеримые с единицей, были названы «иррациональными» потому, что их действительно считали не поддающимися логическому пониманию. На самом деле это не так. Еще у древнегреческого математика Евклида встречаются такие определения, из которых видно, что он отнюдь не считал «иррациональные числа» «неразумными», «нелогичными».

Строгая теория иррациональных чисел была построена впервые лишь во второй половине XIX века немецким математиком Дедекиндом. Со строгой теорией иррациональных чисел можно ознакомиться, например, по книге А. Н. Колмогорова и П. С. Александрова «Введение в теорию функций действительного переменного».

Примечание:

Примем к сведению без доказательства, что правила и формулы, выведенные для рациональных чисел, остаются в силе и для всех действительных чисел. Например, правила умножения и деления степеней, формулы умножения, свойства пропорций, свойство ряда равных отношений и т. д.

Некоторые понятия и предложения элементарной теории множеств

О бесконечных множествах

В математике постоянно приходится иметь дело с бесконечными множествами.

Приведем несколько примеров таких множеств:

1) множество всех натуральных чисел;
2) множество всех четных чисел;
3) множество всех простых чисел;
4) множество всех, рациональных чисел;
5) множество всех иррациональных чисел;
6) множество всех действительных чисел;
7) множество всех различных прямоугольных треугольников с гипотенузой, равной единице;
8) множество всех различных квадратных уравнений с действительными числовыми коэффициентами.

Введем понятие о взаимно однозначном соответствии.

Мы уже знаем, что каждому действительному числу соответствует определенная точка числовой оси и, наоборот, каждой точке числовой оси соответствует определенное действительное число. Имея это в виду, говорят, что между множеством действительных чисел и множеством точек числовой оси имеет место взаимно однозначное соответствие.

Приведем другой пример взаимно однозначного соответствия.

Между множеством всех целых положительных чисел и множеством целых отрицательных чисел можно установить взаимно однозначное соответствие. Например, каждому целому положительному числу можно поставить в соответствие число, ему противоположное.

Определение:

Если между элементами двух множеств можно установить взаимно однозначное соответствие, то такие два множества называются эквивалентными.

Пример:

Множество точек числовой оси и множество действительных чисел эквивалентны. Каждой точке числовой оси соответствует одно и только одно определенное действительное число и, наоборот, каждому действительному числу соответствует одна и только одна определенная точка числовой оси.

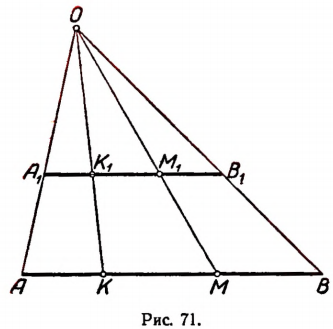
Пример:

Множество точек отрезка АВ (рис. 71) и множество точек отрезка 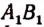— эквивалентны.

Каждой точке М отрезка А В можно поставить в соответствие одну и только одну точку отрезка лежащую на луче ОМ. Наоборот, каждой точке отрезка можно поставить в соответствие одну и только одну точку К отрезка АВ, лежащую на луче ОК.

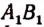
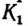
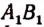
Пример:

Множество всех целых положительных чисел

эквивалентно множеству всех положительных четных чисел

В самом деле, мы можем поставить в соответствие каждому целому числу число, вдвое большее его. Наоборот, каждому четному числу мы можем поставить в соответствие число, вдвое меньшее его.

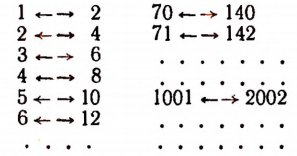
Взаимно однозначное соответствие между рассмотренными множествами (пример 3) мы можем записать в виде следующей таблицы:

Относительно двух эквивалентных бесконечных множеств говорят также, что они имеют одинаковую мощность. Другими словами, два бесконечных множества имеют одинаковую мощность, если эти множества эквивалентны.

Счетные множества и множества мощности континуума

Множество, эквивалентное множеству всех целых положительных чисел, называется счетным множеством. Например, множество всех положительных четных чисел есть счетное множество. Множество всех положительных нечетных чисел также будет счетным, так как оно тоже эквивалентно множеству всех целых положительных чисел.

Так как всякое множество эквивалентно самому себе, то и множество целых положительных чисел также является счетным множеством.

Множество, эквивалентное множеству всех действительных чисел, называется множеством мощности континуума.

Множество точек числовой оси эквивалентно множеству действительных чисел. Поэтому множество точек числовой оси также имеет мощность континуума.

Приведем еще примеры множеств, имеющих мощность континуума.

Пример:

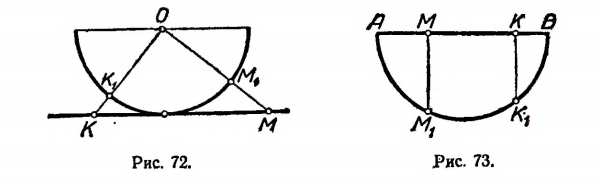
Множество точек полуокружности имеет мощность континуума. В самом деле, легко убедиться в том, что множество точек полуокружности эквивалентно множеству точек числовой оси. Каждой точке полуокружности (рис. 72) можно поставить в соответствие одну и только одну точку М числовой оси, лежащую на луче . Наоборот, каждой точке К числовой оси можно поставить в соответствие одну и только одну точку полуокружности, лежащую на луче ОК.

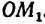
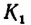
Пример:

Множество точек любого отрезка прямой имеет мощность континуума.

Доказательство:

Множество точек отрезка прямой эквивалентно множеству точек полуокружности, построенной на этом отрезке как на диаметре.

В самом деле, каждой точке М отрезка АВ (рис. 73) можно поставить в соответствие одну и только одну определенную точку полуокружности, лежащую на перпендикуляре к прямой АВ, восставленном из точки М. Далее, каждой точке полуокружности можем поставить в соответствие одну и только одну точку К отрезка АВ, лежащую на перпендикуляре, опущенном из точки на прямую АВ.

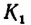
Но ранее было доказано, что множество точек полуокружности имеет мощность континуума. Следовательно, и мощность множества точек любого отрезка прямой также ийеет мощность континуума, что и требовалось доказать.

Так как всякое множество эквивалентно самому себе, то множество действительных чисел также имеет мощность континуума.

Примем к сведению без доказательства следующее.

С теорией множеств можно ознакомиться, например, по книге А. Н. Колмогорова и С. Ф. Фомина «Элементы теории функций и функционального анализа».

Дополнение к иррациональным числам

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник