Что такое отсчетный эллипсоид
Системы высот в геодезии
Понятие высоты, несмотря на кажущуюся очевидность, является одним из наиболее сложных и тонких понятий геодезии. Это связано с двойственным смыслом высоты: с одной стороны, это расстояние между точками в пространстве, т.е. чисто геометрическое понятие; с другой стороны, в физическом понимании, это величина, определяющая энергетический уровень той или иной точки в поле силы тяжести.
Если две точки лежат на одной отвесной линии, геометрическую высоту можно измерить непосредственно как расстояние между ними; так измеряют высоты различных предметов (высота геодезического сигнала, инструмента над центром, высота человека, дерева, дома и т.д.). Очевидно, что геодезическую высоту, т.е. высоту в геометрическом смысле, так измерить нельзя: в точке поверхности Земли неизвестны ни направление нормали к эллипсоиду, вдоль которой нужно измерять высоту, ни положение отсчетной точки на эллипсоиде, которая к тому же физически недоступна, поскольку эллипсоид проходит, как правило, внутри Земли.
Физическое понятие высоты связано с работой в поле силы тяжести. Так, если точки лежат на одной уровенной поверхности, например, на поверхности какого-либо водоема, где отсутствуют течения, естественно, считать, что высоты этих точек одинаковы. Если же вода течет от одной точки к другой, говорят, что высота первой точки больше. В этом случае мерой высоты выступает работа, которую совершает сила тяжести при перемещении водной часы, т.е. разность потенциалов между указанными точками. Поскольку потенциал на уровенной поверхности постоянен, разность потенциалов любых точек, лежащих на двух различных уровенных поверхностях, всегда постоянна. Поэтому разность потенциалов является мерой высоты или высотой в физическом понимании. Как известно, разность потенциалов можно получить в результате геометрического нивелирования и измерений силы тяжести.
Еще одной причиной, по которой высоту рассматривают и изучают отдельно от плановых координат, является различие в методах получения этих величин: до недавнего времени плановые координаты находили из обработки линейных и угловых измерений, выполненных на поверхности Земли, а высоты преимущественно из геометрического нивелирования, сопровождаемого измерениями силы тяжести. Определение высоты по измерениям расстояний и вертикальных углов затруднено из-за влияния вертикальной рефракции, из-за чего вертикальные углы измеряют со значительно меньшей точностью, чем горизонтальные.
Спутниковые методы позволяют определить прямоугольна координаты точек поверхности Земли, по которым, используя зависимости математических формул, можно найти геодезические координаты. Однако так можно найти только высоту в геометрическом понимании, поскольку прямоугольные координаты не содержат информации о поле силы тяжести. Кроме того, из-за тропосферных влияний и методических особенностей высота и в этом случае определяется с несколько меньшей точностью, чем плановые координаты.
Что такое высота и где ее начало
Для определения положения точки, находящейся на физической поверхности Земли относительно исходной уровенной поверхности, помимо плоских координат, необходима третья координата — высота Н.
Высота – это измерение объекта или его местоположения, отмеряемое в вертикальном направлении. Высота в любой точки земной поверхности отсчитывается от разных поверхностей, таких как геоид, квазигеоид или референц-эллипсоид.
Геоид, квазигеоид и эллипсоид вращения
Геоид — это образованная основной уровенной поверхностью замкнутая фигура принимаемая за обобщенную поверхность Земли. Поверхность геоида является одной из уровенных поверхностей потенциала силы тяжести. Эта поверхность, мысленно продолженная под материками, образует замкнутую фигуру, которую принимают за сглаженную фигуру Земли. Часто под геоидом понимают уровенную поверхность, проходящую через некоторую фиксированную точку земной поверхности у берега моря. Понятие о геоиде сложилось в результате длительного развития представлений о фигуре Земли как планеты, а самый термин «геоид» предложен И. Листингом в 1873 г. От геоида отсчитывают абсолютные высоты. По современным данным, средняя величина отступления геоида от наиболее удачно подобранного эллипсоида составляет около ±50 м, а максимальное отступление не превышает ±100 м. Высота геоида в сумме с ортометрической высотой определяет высоту Н соответственной точки над земным эллипсоидом. Поскольку распределение плотности внутри Земли с необходимой точностью неизвестно, высоту Н в геодезической гравиметрии и геодезии, согласно предложению М. С. Молоденского, определяют как сумму нормальной высоты и высоты квазигеоида. Для точного определения поверхности геоида какой-либо точки необходимо выполнить комплекс измерений, непосредственно на поверхности геоида. Что практически не возможно, либо в соответствующей точке на физической поверхности Земли с учетом распределения масс в этом месте, что также не предоставляется возможным. По этой причине было предложено вместо поверхности геоида использовать квазигеоид.
Квазигеоид — это поверхность близкая к поверхности геоида, определяемая только по результатам измерений на земной поверхности без привлечения данных по распределению масс. Поверхность квазигеоида определена значениями потенциала силы тяжести на земной поверхности, и для изучения квазигеоида результаты измерений не нужно редуцировать внутрь притягивающей массы. Квазигеоид отступает от геоида в высоких горах на 2–4 м, на низменных равнинах — на 0,02-0,12 м, на морях и океанах поверхности геоида и квазигеоида совпадают.
Фигуру квазигеоида определяют методом астрономо-гравиметрического нивелирования или через предварительное определение возмущающего потенциала по материалам наземных гравиметрических съёмок и наблюдений за движением искусственных спутников Земли. Последние данные необходимы в связи с недостаточной гравиметрической изученностью некоторых областей Земли Поверхность геоида, из-за ее сложности, математически никак не выражается, поэтому на ней нельзя решать геодезические задачи. Для решения таких задач взамен поверхности геоида принимают поверхность эллипсоида вращения.
Эллипсоида вращения — это близкая по форме к геоиду поверхность, но математически правильная, на которую можно перенести результаты измерений, выполненных на физической поверхности Земли. Эллипсоид вращения, размеры которого подбираются при условии наилучшего соответствия фигуре квазигеоида для Земли в целом (общеземной эллипсоид) или отдельных её частей (референц-эллипсоид). Для России принят референц-эллипсоид Крассовского форма и размеры которого были вычислены советским геодезистом А. А. Изотовым, и который в 1940 году назван именем Ф. Н. Красовского.
Высота точки местности в географии, топографии и геодезии может измеряться от разных уровней отсчёта:
1. Абсолютная высота отсчитывается от уровня моря или геоида (линия НА и линия НВ);
2. Относительная высота (превышение) отсчитывается от какого-либо условного уровня (линия НС);
3. Геодезическая (эллипсоидальная) высота — высота относительно эллипсоида вращения.
Абсолютная и относительная высоты
В нашей стране с 1946 г. счет абсолютных высот ведется от нуля Кронштадтского футштока соответствующего среднему уровню Балтийского моря в спокойном его состоянии (Балтийская система высот). Вся нивелирная сеть на территорию России опирается на один исходный пункт, не имеет внешнего контроля и уравнивается как свободная система. В середине 1980-х в связи с предстоящим строительством гидротехнического комплекса защиты Ленинграда (ныне Санкт-Петербурга) от наводнений были созданы дублеры в Кронштадте и г. Ломоносове (на основе репера № 6521 и маяка Шепелевский)
Высоты, отсчитанные от иной уровенной поверхности, называются относительными на рисунке изображены линией НС. При съемке небольших участков, при обмерных работах, а также на стройплощадке часто применяют относительную или условную систему отсчета высот.
Что такое превышение
Численное значение высоты точки называется отметкой точки. Разность высот двух точек, называется превышением. Превышение h точки В над точкой А, равное разности высот точек А и В, определяется как h = НВ – НА. Зная высоту точки А, для определения высоты точки В на местности измеряют превышение hAB. Высоту точки В вычисляют по формуле HВ = HA + hAB. Измерение превышений и последующее вычисление высот точек называется нивелированием.
Геодезическая высота
Геодезической (эллипсоида́льной) высотой некоторой точки физической поверхности земли называется отрезок нормали к эллипсоиду от его поверхности до данной точки. Вместе с геодезическими широтой и долготой (B и L соответственно) она определяет положение точки относительно заданного эллипсоида. Физически эллипсоида не существует, следовательно геодезическая высота не может быть непосредственно измерена наземными методами. Определить её возможно с помощью спутниковых измерений, а также посредством обработки рядов триангуляции, астрономо-геодезического нивелирования.
Как видно из определения геодезическая высота зависит от расположения и параметров выбранного эллипсоида, поэтому геодезическую высоту разделяют на две части. Одна из них характеризует физическую поверхность Земли относительно уровенной поверхности (информацию о ней получают в большей степени нивелированием), вторая, более гладкая, характеризует отличие отсчётного эллипсоида от геоида. Первую часть называют гипсометрической, а вторую — гладкой или геоидальной частью. Уровенная поверхность имеет несравненно более плавную форму в сравнении с физической, следовательно геоидальная часть меняется гораздо медленнее гипсометрической.
Системы геодезических высот
Ортометрическая высота точки — это расстояние (H) вдоль отвесной линии от точки до поверхности геоида. Ортометрическая высота для практических целей является «высотой над уровнем моря». Чтобы вычислить значение ортометрической высоты, нужно знать плотность пород вдоль силовой линии или измерять силу тяжести внутри Земли. Поэтому ортометрическую высоту нельзя найти по измерениям только на поверхности Земли. Альтернативой ортометрической высоте являются нормальная высота. Ортометрические высоты по Гельмерту используют многие европейские страны, Турция и страны Американского континента. Поскольку гравитация не является постоянной на больших площадях, ортометрическая высота также не является постоянной. Так на территории США гравитация на 0,1% сильнее на севере Соединенных Штатов, чем на юге, поэтому ровная поверхность, имеющая ортометрическую высоту в 1000 метров в Монтане, будет иметь высоту в 1001 метр в Техасе.
Нормальные высоты — это высоты от поверхности квазигеоида, один из нескольких типов высоты. Нормальная высота точки вычисляется из геопотенциальных чисел путем деления геопотенциального числа точки, т. е. ее разности геопотенциалов с уровнем моря, на среднюю нормальную гравитацию, вычисленную вдоль отвеса точки. (Точнее, вдоль эллипсоидной нормали, усредняя по диапазону высот от 0-эллипсоид-H*; процедура, таким образом, рекурсивна. Нормальные высоты, таким образом, зависят от выбранного опорного эллипсоида. Система нормальных высот принята в России, странах СНГ и некоторых европейских странах (Швеция, Германия, Франция и др.). Нормальные значения гравитации можно вычислить через плотность земной коры вокруг отвеса. Нормальные высоты занимают видное место в теории гравитационного поля Земли, разработанной школой М. С. Молоденского. Эталонная поверхность, с которой измеряются нормальные высоты, называется квазигеоидом, представляющим собой «средний уровень моря», аналогичный геоиду и близкий к нему, но лишенный физической интерпретации эквипотенциальной поверхности. В геодезии (топографии) нормальную высоту называют абсолютной, а разность нормальных высот — относительной высотой. Численное значение абсолютной высоты принято называть отметкой.
Геопотенциальное число ― это та работа, которую нужно совершить, чтобы подняться от уровня моря до точки Р поверхности Земли.
Динамическая высота — это геопотенциальное число, переведенное в линейную меру, получить его можно разделив геопотенциальное число на любое постоянное значение С силы тяжести. Выбирая в качестве С разные значения постоянной, можно построить разные системы динамических высот. Динамические вы соты были введены К.Ф.Гауссом, который предложил рассматривать высоты как геопотенциальные числа, т.е. принять С = 1. Динамическая высота постоянна, если следовать одному и тому же гравитационному потенциалу, когда они перемещаются с места на место. Из-за изменения силы тяжести поверхности, имеющие постоянную разницу в динамической высоте, могут быть ближе или дальше друг от друга в различных местах. Динамические высоты обычно выбираются так, чтобы они имели сопряжения с геоидом. Когда оптическое выравнивание выполнено, путь близко соответствует следующему значению динамической высоты по горизонтали, но не ортометрической высоте для вертикальных изменений, измеренных на выравнивающем стержне. Таким образом, небольшие поправки должны быть применены к полевым измерениям, чтобы получить либо динамическую высоту, либо ортометрическую высоту, обычно используемую в технике. Паспорта данных Национальной Геодезической службы США дают как динамические, так и ортометрические значения. Динамическая высота может быть вычислена с использованием нормальной силы тяжести на 45-градусной широте и геопотенциального числа местоположений.
Что такое отсчетный эллипсоид
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Глобальные навигационные спутниковые системы
Методы преобразований координат определяемых точек
Global navigation satellite system and global positioning system. Coordinate systems. Methods of transformations for determinated points coordinate
Дата введения 2009-09-01
Сведения о стандарте
1 РАЗРАБОТАН 29 Научно-исследовательским институтом Министерства обороны Российской Федерации
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 363 «Радионавигация»
ВНЕСЕНЫ поправки, опубликованные в ИУС N 4, 2011 год, ИУС N 6, 2011 год, ИУС N 9, 2013 год
Поправки внесены изготовителем базы данных
1 Область применения
Настоящий стандарт распространяется на системы координат, входящие в состав систем геодезических параметров «Параметры Земли», «Мировая геодезическая система» и координатной основы Российской Федерации, и устанавливает методы преобразований координат и их приращений из одной системы в другую, а также порядок использования числовых значений элементов трансформирования систем координат при выполнении геодезических, навигационных, картографических работ с использованием аппаратуры потребителей глобальных навигационных спутниковых систем.
2 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
2.1 большая полуось эллипсоида : Параметр, характеризующий размер эллипсоида.
2.2 отсчетный эллипсоид: Эллипсоид, принятый для обработки геодезических измерений и установления системы геодезических координат.
2.3 система геодезических координат: Система параметров, два из которых (геодезическая широта и геодезическая долгота) характеризуют направление нормали к поверхности отсчетного эллипсоида в данной точке пространства относительно плоскостей его экватора и начального меридиана, а третий (геодезическая высота) представляет собой высоту точки над поверхностью отсчетного эллипсоида.
2.4 геодезическая широта: Угол между нормалью к поверхности отсчетного эллипсоида, проходящей через заданную точку, и плоскостью его экватора.
2.5 геодезическая долгота: Двугранный угол между плоскостями геодезического меридиана данной точки и начального геодезического меридиана.
2.6 геодезическая высота: Высота точки над поверхностью отсчетного эллипсоида.
2.7 плоскость геодезического меридиана: Плоскость, проходящая через нормаль к поверхности отсчетного эллипсоида в данной точке и параллельная его малой оси.
2.8 плоскость астрономического меридиана: Плоскость, проходящая через отвесную линию в данной точке и параллельная оси вращения Земли.
2.9 плоскость начального меридиана: Плоскость меридиана, от которого ведется счет долгот.
2.10 геоид: Эквипотенциальная поверхность, совпадающая с поверхностью Мирового океана в состоянии полного покоя и равновесия и продолженная под материками.
2.11 эквипотенциальная поверхность: Поверхность, на которой потенциал имеет одно и то же значение.
2.12 Глобальная система позиционирования (Global Positioning System): Глобальная навигационная спутниковая система, разработанная в США.
2.13 гравитационное поле Земли; ГПЗ: Поле силы тяжести на поверхности Земли и во внешнем пространстве, обусловленное силой притяжения Земли и центробежной силой, возникающей в результате суточного вращения Земли.
2.14 квазигеоид: Математическая поверхность, близкая к геоиду, и являющаяся отсчетной для установления системы нормальных высот.
2.15 космическая геодезическая сеть; КГС: Сеть геодезических пунктов, закрепляющих геоцентрическую систему координат, положение которых на земной поверхности определено по наблюдениям искусственных спутников Земли.
2.16 Мировая геодезическая система (World Geodetic System): Система геодезических параметров, разработанная в США.
2.17 модель гравитационного поля Земли: Математическое описание характеристик гравитационного поля Земли.
2.18 нормальная высота: Высота точки над квазигеоидом, определенная методом геометрического нивелирования.
2.19 нормальное гравитационное поле Земли: Гравитационное поле Земли, представляемое нормальным потенциалом силы тяжести.
2.20 общеземной эллипсоид; ОЗЭ: Эллипсоид, поверхность которого наиболее близка к геоиду в целом, применяемый для обработки геодезических измерений на всей поверхности Земли в общеземной (геоцентрической) системе координат.
2.21 планетарная модель гравитационного поля Земли: Модель гравитационного поля Земли, отражающая гравитационные особенности Земли в целом.
2.22 сжатие эллипсоида : Параметр, характеризующий форму эллипсоида.
2.23 система геодезических параметров Земли: Совокупность числовых параметров и точностных характеристик фундаментальных геодезических постоянных общеземного эллипсоида, планетарной модели гравитационного поля Земли, геоцентрической системы координат и параметров ее связи с другими системами координат.
2.24 фундаментальные геодезические постоянные: Взаимосогласованные геодезические постоянные, однозначно определяющие фигуру общеземного эллипсоида и нормальное гравитационное поле Земли.
2.25 элементы трансформирования систем координат: Параметры, с помощью которых выполняется преобразование координат из одной системы координат в другую.
2.26 плоские прямоугольные координаты: Плоские координаты на плоскости, на которой отображена по определенному математическому закону поверхность отсчетного эллипсоида.
3 Сокращения и обозначения
В настоящем стандарте применены следующие сокращения и обозначения:
3.15 
4 Системы геодезических параметров
4.1 Система геодезических параметров «Параметры Земли»
Система ПЗ включает в себя: фундаментальные геодезические постоянные, параметры ОЗЭ, систему координат ПЗ, закрепляемую координатами пунктов космической геодезической сети, характеристики модели ГПЗ и элементы трансформирования между системой ПЗ и национальными референцными системами координат России. Числовые значения элементов трансформирования между системой ПЗ и национальными референцными системами координат России и порядок их использования при преобразовании систем координат приведены в приложениях А, Б.
1 Постановлением Правительства Российской Федерации от 28 июля 2000 года N 568 для использования в целях геодезического обеспечения орбитальных полетов и решения навигационных задач геоцентрической системе координат «Параметры Земли 1990 года» (ПЗ-90) придан статус государственной системы координат.
2 Распоряжением Правительства Российской Федерации от 20 июня 2007 года N 797-р в целях повышения тактико-технических характеристик глобальной навигационной спутниковой системы ГЛОНАСС, улучшения геодезического обеспечения орбитальных полетов и решения навигационных задач принята к использованию уточненная версия государственной геоцентрической системы координат «Параметры Земли 1990 года» (ПЗ-90.02).
3 Числовые значения элементов трансформирования между системами координат ПЗ-90.02 и ПЗ-90 и порядок их использования при преобразовании систем координат приведены в приложении Д.
Теоретическое определение системы координат ПЗ основывается на следующих положениях:
а) начало системы координат расположено в центре масс Земли;
б) ось направлена в Международное условное начало;
в) ось лежит в плоскости начального астрономического меридиана, установленного Международным бюро времени;
г) ось дополняет систему до правой системы координат.
Положения точек в системе ПЗ могут быть получены в виде пространственных прямоугольных или геодезических координат.
Геодезические координаты относятся к ОЗЭ, размеры и форма которого определяются значениями большой полуоси и сжатия.
Геодезия
Для студентов аспирантов и преподавателей
Разделы
Общий земной эллипсоид
При изучении фигуры Земли с давних пор поступают следующим образом. Сначала определяют форму и размеры некоторой модели Земли, поверхность которой сравнительно проста, хорошо изучена в геометрическом отношении, удобна для решения на ней разнообразных задач геодезии и картографии и наиболее полно характеризует в первом приближении форму и размеры реальной Земли. Затем, приняв поверхность этой модели Земли за отсчетную, определяют относительно нее высоты точек поверхности изучаемой фигуры — геоида (квазигеоида) или реальной Земли — и таким образом получают данные, характеризующие форму и размеры конкретной фигуры.
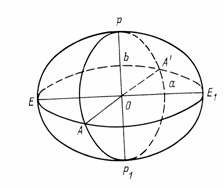
При решении задач высшей геодезии за такую модель Земли принимают эллипсоид вращения с малым полярным сжатием, называемый общим земным эллипсоидом (рис. 4). Его поверхность может быть получена вращением полуэллипса РЕР1 вокруг его малой оси РР1.
Форма и размеры земного эллипсоида характеризуются большой а и малой bполуосями, а чаще большой полуосью а и полярным сжатием а,
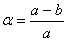
или большой полуосью а и первым эксцентриситетом е меридианного эллипса:
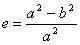
Для того чтобы общий земной эллипсоид возможно точнее характеризовал форму и размеры всей Земли, его параметры а, а определяют с учетом следующих условий:
1) центр общего земного эллипсоида должен совпадать с центром масс Земли, а его малая ось — с осью вращения Земли;
2) объем эллипсоида должен быть равен объему геоида (квазигеоида);
3) сумма квадратов отклонений по высоте поверхности эллипсоида от поверхности геоида (квазигеоида) должна быть наименьшей.
До недавнего времени, т. е. до начала освоения человеком космического пространства, параметры земного эллипсоида получали, выполняя так называемые градусные измерения. С этой целью прокладывали ряды триангуляции по направлению меридианов и параллелей на разных широтах, на конечных пунктах которых определяли астрономические широты, долготы, а также азимуты сторон. Для вывода надежных значений параметров общего земного эллипсоида градусные измерения, в принципе, необходимо было выполнить на всей поверхности Земли, включая Мировой океан. Кроме того, астрономические широты, долготы и азимуты следовало исправить поправками за влияние уклонений отвесных линий, которые, как правило, были неизвестны.
В прошлом градусные измерения велись только на материках, т. е. на незначительной части земной поверхности. Градусные измерения разных стран не имели общих связей, выполнялись по разным программам с разной точностью, обрабатывались в разных системах координат. Все это затрудняло их совместное использование и отрицательно сказывалось на точности выводов размеров земного эллипсоида.
В течение полутора веков ученые многих стран занимались определением размеров земного эллипсоида, используя имеющиеся в разном объеме разной точности и содержания градусные измерения. Приведем некоторые результаты таких определений (табл.» 1).
Эллипсоид Деламбра имеет только лишь историческое значение как основа для установления метрической системы мер. На поверхности эллипсоида Деламбра расстояние от полюса до экватора точно составляет 10000 км, так как в то время 1 м