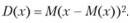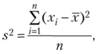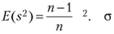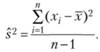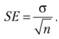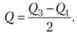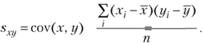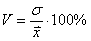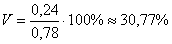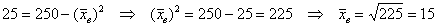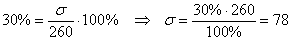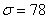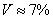Что такое оценка дисперсии

Дисперсия и ее оценка

Определение дисперсии случайных величин

Дисперсия – норма, отражающая, с точки зрения теории, ожидаемое отклонение случайной величины от ее математического ожидания.

В математической статистике она определяется в качестве центрального момента второго порядка. Приведем формулу дисперсии:

где М(х) – математическое ожидание, а D(х) – дисперсия.

На основе данной формулы можно вывести другую, которая дает оценку дисперсии:

В первой формуле оценка математического ожидания не смещена, но во второй формуле дисперсия является выборочной. Т.е. эта оценка дает характеристику величине дисперсии данной выборки, не для популяции данных. Обычно для эксперимента необходимо оценить популяционный характер математического ожидания и дисперсию.

Так как вторая формула предполагает сравнение эмпирических знаний не с истинной величиной, а с оценочной, то происходит смещение оценки дисперсии. Способами дифференциального исчисления определено: ожидаемая величина оценки дисперсии по второй формуле описывает соотношение:

Данная формула отражает выборочную дисперсию. Из нее следует, что при наличии 10 выборочных значений случайной величины идет занижение значения. Получается 9/10 дисперсий анализируемой величины для генеральной совокупности. Если увеличить объем в десять раз, то уменьшиться величина смещения до одной сотой, и при этому полученный результат будет отличаться от ожидаемого значения. При помощи третьей формулы можно рассчитать несмещенную оценку дисперсии:

Данная формула называется популяционной дисперсией, или дисперсией генеральной совокупности. Эту формулу используют для расчета генеральной совокупности, третью – для определения вариантов внутри выборки и выход за пределы имеющихся значений, который не предполагается теорией.

Характеристика оценивания стандартного отклонения

Иногда для оценивания важна не сама дисперсия, а оценка стандартного отклонения. Эти две величины связаны однозначным соотношением. Оценивание стандартного отклонения также применяется для выборки и генеральной совокупности, как и дисперсия. Оценка данной величины является предпочтительной, так как она удобна для восприятия из-за своей размерности. Помимо этого, эту величину используют для вычисления стандартной ошибки. Формула выглядит следующим образом:

где SE – стандартная ошибка.

Данная статистика необходима для интервальной оценки исследуемой случайной величины.

Характеристика оценки полумежквартильного интервала

Это еще один способ оценивания вариантов в распределении случайной величины. Ее обозначают Q. Она используется в качестве альтернативы стандартного отклонения, несмотря на то, что они связаны соотношением Q = 0,67σ.

Квартиль – это вариант названия квантиля распределения.

При соответствии медианы с половиной распределения, то квартиль равен четверти. Т.е. первая четверть – это первый квартиль, половина – второй квартиль, три четвертых – третий, общая сумма величины – четвертый квартиль. Формула межквартильного интервала выглядит следующим образом:

Данную оценку используют, например, в сенсорной психофизике при оценивании порога способом констант.

Характеристика ковариации

Иногда необходимо оценить не одну дисперсию, а две (х,у). Такая статистика называется ковариацией. Ее формула выглядит следующим образом:

Она определяет степень связи между двумя переменами. Отличительная особенность ковариации – это ее выражение и в положительных и в отрицательных числах. Так как ковариация зависит от размерности, то оценить степень между переменными невозможно. Поэтому в качестве меры двух переменных используют термин «корреляция». Ее величина может быть определена за счет деления ковариации на произведение стандартных отклонений двух случайных величин, между которыми вычисляют ковариацию.

Источник

Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Источник

Выборочная несмещенная дисперсия

Приветствую посетителей блога statanaliz.info. В данной статье рассмотрим, что такое «выборочная несмещенная дисперсия».

Понятие о сплошном и выборочном наблюдении

С точки зрения охвата объекта исследования, статистический анализ можно разделить на два вида: сплошной и выборочный. Сплошной статанализ предполагает изучение генеральной совокупности данных, то есть всего явления во всем его многообразии без распространения выводов на другие элементы, не входящие в анализируемую совокупность. Из названия данного типа явствует, что наблюдению подвергаются тотально все элементы. Результат анализа распространяется на всю генеральную совокупность без каких-либо допущений и поправок на ошибку. Данный тип статистического исследования является наиболее полным и точным, так как дополнительные знания почерпнуть уже неоткуда – информация собрана со всех элементов объекта исследования. Это бесспорный плюс.

Отличным примером сплошного наблюдения является перепись населения. «Всесоюзная перепись населения» — красиво звучало! Кстати, советская статистика, как и наука в целом, была одной из самых лучших в мире. Денег на проведение сплошных обследований не жалели, так как при СССР статистика выполняла свою прямую функцию – исследовала реальность, без чего невозможно было строить «светлое будущее». При этом советские ученые-статистики справедливо критиковали буржуазную статистику за то, что те скрывают от народа реальное положение дел и используют статистику для промывки мозгов. Об этом, кстати, писали и сами буржуи. Более практичный пример сплошного наблюдения – опрос жителей многоэтажного дома на предмет заваривания мусоропровода. Опрашиваются все, результат дает вполне однозначный ответ об отношении жителей к мусоропроводу. Ошибки в выводах маловероятны.

Как бы там ни было, у сплошного наблюдения есть отрицательное качество: на организацию и проведение исследования могут потребоваться значительные ресурсы. Одно дело взять пробу из партии товаров, другое – проверять всю партию. Одно дело опросить тысячу прохожих на улице, совсем другое – организовать перепись населения.

В противовес сплошному придумали выборочное наблюдение. Название метода точно отражает его суть: из генеральной совокупности отбирается и анализируется только часть данных, а выводы распространяют на всю генеральную совокупность. Отбор данных происходит таким образом, чтобы выборка была репрезентативной, то есть, сохранила внутреннюю структуру и закономерности генеральной совокупности. Если это условие не соблюдено, то дальнейший анализ во многом теряет смысл.

Сам анализ выборочных данных происходит так же, как и при сплошном наблюдении (рассчитываются различные показатели, делаются прогнозы и т.д.), только с поправкой на ошибку. Это значит, что рассчитывая тот или иной показатель, мы понимаем, что при повторной выборке его значение будет другим. К примеру, провели опрос общественного мнения. Опрос показал, что за кандидата N желают проголосовать 60% опрошенных. Если провести еще один такой же опрос, даже в том же месте, то результат будет отличаться. То есть, взяв первое значение 60%, следует понимать, что с той или иной вероятностью оно могло быть, скажем, и 58%, и 62%. Точность и разброс выборочных показателей зависят от характера данных и их количества.

У выборочного наблюдения есть один существенный плюс и один минус, однако по сравнению со сплошным наблюдением крайности меняются местами. Плюс заключается в том, что для проведения выборочного обследования требуется гораздо меньше ресурсов. Минус – в том, что выборочное наблюдение всегда ошибочно. Поэтому основная задача проведения выборочного наблюдения – добиться максимальной точности при приемлемых затратах на его проведение.

Выборочная несмещенная дисперсия

И вот, стало быть, дисперсия. Дисперсия, как и доля или средняя арифметическая, также меняет свое значение от выборки к выборке, но здесь есть интересная особенность. Дисперсия ведь рассчитывается от средней величины, а она в свою очередь, тоже рассчитывается по выборке, то есть является ошибочной. Как же это обстоятельство влияет на саму дисперсию?

Если бы мы знали истинную среднюю величину (по генеральной совокупности), то ошибка дисперсии была бы связана только с нерепрезентативностью, то есть с тем, что данные в выборке оказались бы ближе или дальше от средней, чем в целом по генеральной совокупности. При этом при многократном повторении данные стремились бы к своему реальному расположению относительно средней.

Выборочный показатель, который при многократном повторении выборки стремится к своему теоретическому значению, называется несмещенной оценкой. Почему оценкой? Потому что мы не знаем реальное значение показателя (по генеральной совокупности), и с помощью выборочного наблюдения пытаемся его оценить. Оценка показателя – это есть его характеристика, рассчитанная по выборке.

Теперь смотрим внимательно на выборочную среднюю. Выборочная средняя – это несмещенная оценка математического ожидания, так как средняя из выборочных средних стремится к своему теоретическому значению по генеральной совокупности. Где она расположена? Правильно, в центре выборки! Средняя всегда находится в центре значений, по которым рассчитана – на то она и средняя. А раз выборочная средняя находится в центре выборки, то из этого следует, что сумма квадратов расстояний от каждого значения выборки до выборочной средней всегда меньше, чем до любой другой точки, в том числе и до генеральной средней. Это ключевой момент. А раз так, то дисперсия в каждой выборке будет занижена. Средняя из заниженных дисперсий также даст заниженное значение. То есть при многократном повторении эксперимента выборочная дисперсия не будет стремиться к своему истинному значению (как выборочная средняя), а будет смещена относительно истинного значения по генеральной совокупности.

Отклонение выборочной средней от генеральной показано на рисунке.

Несмещенность оценки – одна из важных характеристик статистического показателя. Смещенная оценка показателя заранее говорит о тенденции к ошибке. Поэтому показатели стараются оценивать таким образом, чтобы их оценки были несмещенными (как у средней арифметической). Чтобы решить проблему смещенности выборочной дисперсии, в ее расчет вносят корректировку – умножают на n/(n-1), либо сразу при расчете в знаменатель ставят не n, а n-1. Получается так.

Выборочная смещенная дисперсия:

Выборочная несмещенная дисперсия:

Под выборочной дисперсией понимают, как правило, именно несмещенный вариант.

Теперь посмотрим на практическую сторону отличия смещенной и несмещенной дисперсии. Соотношение между выборочной и генеральной дисперсией составляет n/n-1. Несложно догадаться, что с ростом n (объема выборки) данное выражение стремится к 1, то есть разница между значениями выборочной и генеральной дисперсиями уменьшается.

Так, в выборке из 11 наблюдений относительная разница составляет 11/10 = 10%. При 21 наблюдениях, отличие сокращается до 5%, при 31 наблюдении – до 3,3%, при 51 – до 2%, при 101 – до 1%. Короче, при достаточно большой выборке данных (50 и выше наблюдений) относительная разница между смещенной и несмещенной дисперсией практически исчезает. Оценка параметра, когда с ростом выборки его отклонение от теоретического значения уменьшается, называется асимптотически несмещенной оценкой.

При переходе к среднеквадратичном отклонению по выборке (корень из выборочной дисперсии) разница становится еще меньше.

Таким образом, эффект смещенной дисперсии проявляется в небольших выборках. В больших выборках можно использовать генеральную дисперсию, что как бы не усложняет и не упрощает жизнь. Вручную сейчас никто не считает. Все легко посчитать в Excel. Но понимать различие в терминологии и в сути показателей все же следует.

Из данной статьи неплохо бы усвоить следующее.

1. Формула генеральной дисперсии в выборке дает смещенную оценку.

2. В знаменателе несмещенной оценки n-1 вместо n.

3. При большом объеме выборки (от 100 наблюдений) разница между смещенной и несмещенной дисперсиями практически исчезает.

4. Стандартное отклонение по выборке – это корень из выборочной дисперсии.

Источник

6. Формула для вычисления дисперсии.
Среднее квадратическое отклонение. Коэффициент вариации

В первой части урока мы рассмотрели размах вариации, среднее линейное отклонение и дисперсию, и продолжение темы в заголовке. Многие из этих показателей фигурируют в теории вероятностей, и если вы зашли с поисковика именно за ними, то сразу ссылка на нужную статью: Дисперсия дискретной случайной величины – там же всё остальное.

Ну а здесь на повестке дня Математическая статистика (организационный урок для «чайников»), и мы продолжаем изучать показатели вариации:

Всё с формулами, примерами решений и техникой рациональных вычислений.

И снова о дисперсии.

На предыдущем занятии мы рассчитывали дисперсию по определению:
– для несгруппированных данных и
– для дискретного либо интервального вариационного ряда.

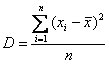
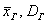
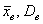
Если известно, генеральная ли нам дана совокупность или выборочная, то хорошим тоном считается поставить подстрочные индексы: либо .

Расчёт дисперсии по определению прост и реально используется на практике, но существует ещё более простой и удобный способ вычисления – по формуле, которую несложно вывести из определения:

– дисперсия равна разности средней арифметической квадратов всех вариант статистической совокупности и квадрата средней самих этих вариант.

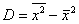
ОСМЫСЛЕННО повторяем ВСЛУХ и вникаем! … Карл украл у Клары кораллы, а Клара украла у Карла кларнет 🙂

Если что-то не очень понятно, то сейчас всё станет на свои места:

Для несгруппированных вариант 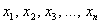выборочной совокупности формула детализируется следующим образом:

и для готового вариационного ряда – так: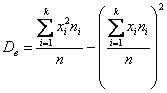
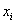
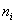
, где – кратные (одинаковые) варианты дискретного ряда либо середины интервалов интервального ряда, а – соответствующие частоты.

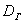
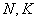
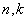
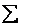
Для генеральной дисперсии формулы те же, только с буквами вместо . Во многих случаях удобно использовать просто значок суммирования – без переменной-«счётчика», поскольку в контексте той или иной задачи и так понятно, что суммируется.

И начнём мы со знакомой подопытной задачи:

В результате 10 независимых измерений получены опытные данные, которые представлены в таблице:

Это данные из Примера 13, и на этот раз нам требуется вычислить дисперсию с помощью формулы. Напоминаю, что там мы её рассчитали по определению и получили результат 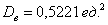, таким образом, ответ известен заранее, и это всегда круто. Всегда, когда он правильный.

Решение: используем формулу .
Для этого нужно найти выборочную среднюю, повторим действие: ,
вычислить квадраты всех вариант: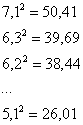

и их сумму: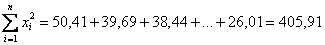
Результаты вычислений удобно заносить в таблицу: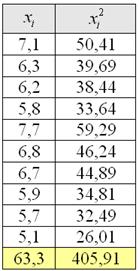

Осталось применить формулу: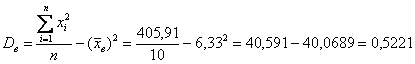
, что и требовалось увидеть.

Ответ:

Теперь случай сформированного вариационного ряда. В Примере 14 мы потренировались на дискретном ряде, и сейчас очередь интервального:

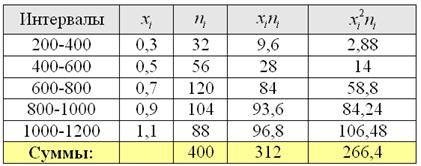
С целью изучения вкладов в Сбербанке города проведено выборочное исследование, в результате которого получены следующие данные:

Вычислить выборочную дисперсию и среднее квадратическое отклонение, оценить соответствующие показатели генеральной совокупности.

Автор задачи заботливо подсчитал объем выборки 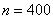, но не «закрыл» крайние интервалы. Такая вещь уже встречалась, и решение мы начинаем с этого закрытия. Поскольку длины внутренних интервалов составляют д.е., то логично рассмотреть такую же длину и по краям, то бишь, интервалы от 200 до 400 и от 1000 до 1200 денежных единиц.

…Возможно, у вас возник вопрос, а как быть, если даны интервалы разной длины? В этом случае принимаем за «эталон» среднюю длину известных интервалов.

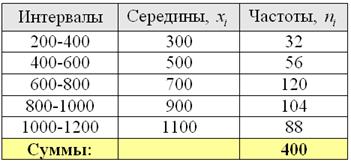
Для расчёта числовых характеристик перейдём к дискретному вариационному ряду, выбрав в качестве вариант 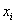середины интервалов, которые здесь видны устно:

В тяжёлых случаях суммируем концы интервалов и делим их пополам, например: .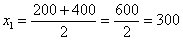

Кроме того, варианты целесообразно уменьшить в 1000 раз, поскольку в ходе дальнейших вычислений будут получаться гигантские числа. С современными вычислительными мощностями, это, конечно, не проблема, но смотреться будет некрасиво.

Сначала вычислим выборочную среднюю. Этот алгоритм уже обкатан: находим произведения 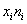, их сумму:

и по соответствующей формуле:
тыс. д.е. или 780 д.е. – средний размер вклада.

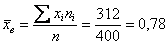
Примечание: далее для компактной записи я буду использовать просто значок 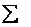– без переменной-«счётчика».

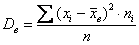
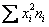
Теперь дисперсия. Её никто не запрещает рассчитать по определению , но заметьте, насколько легче формула – для её применения всего-то лишь нужно рассчитать произведения и их сумму (правый столбец таблицы). Несмотря на то, что многие читатели уже освоили технику вычислений в Экселе, я продолжу записывать ролики – мало ли, кто что запамятовал:

Итак, по формуле вычисления дисперсии, получаем:
тыс. д.е. в квадрате (т.к. по определению, дисперсия – есть величина квадратичная).

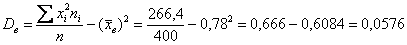
И, чтобы вернуться в размерность задачи, из дисперсии следует извлечь квадратный корень:
тыс. д.е. или 240 денежных единиц. Полученный показатель называется

среднее квадратическое отклонение

Или стандартное отклонение. Оно обозначается греческой буквой «сигма», и коль скоро у нас выборочная совокупность, то добавляем соответствующий подстрочный индекс:

– выборочное среднее квадратическое отклонение.

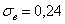
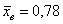
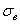
Чем меньше стандартное отклонение (и дисперсия), тем меньше вариация – тем бОльшее количество вариант находится вблизи выборочной средней. Но у нас, как нетрудно «прикинуть на глазок», разброс довольно-таки велик – значительное количество вкладов расположено далековато от , и поэтому значение получилось немалым.

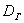
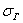
Следующая часть задачи состоит в том, чтобы корректно оценить генеральную дисперсию и генеральное среднее квадратическое отклонение .

В 1-й части урока я рассказал о том, что выборочная дисперсия представляет собой смещённую оценку генеральной дисперсии. Это означает, что если мы будем проводить неоднократные выборки из той же генеральной совокупности, то полученные значения будут систематически занижено оценивать . Обращаю ваше внимание, что это не значит, что будет всегда меньше, чем .

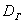
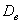
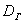
И поэтому выборочную дисперсию, как намекает условие, нужно поправить:
– исправленная выборочная дисперсия

и, соответственно:
или 240,30 д.е. – исправленное среднее квадратическое отклонение.

и – это уже несмещённые оценки генеральной дисперсии и генерального стандартного отклонения соответственно.

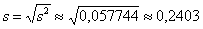
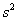
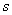
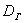
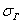
Ввиду большого объёма выборки (более 100 вариант) этой поправкой можно пренебречь, но всё же мы не будем «разбрасываться» 30 «копейками».

Ответ: ; в качестве оценки соответствующих генеральных показателей принимаем и .

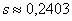
Рассмотренные выше показатели (размах вариации, среднее линейное отклонение, дисперсия, стандартное отклонение) входят в группу абсолютных показателей вариации, которые обладают рядом неудобств. Так, если в прорешанной задаче не уменьшать варианты в 1000 раз, то дисперсия получится в миллион раз больше! Да-да, не 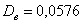, а . И возникает естественное желание привести результаты к некому единому стандарту.

Для этого существуют показатели относительные, и самым известным из них является

коэффициент вариации

– это отношение стандартного отклонения к средней, выраженное в процентах:

И вот теперь совершенно без разницы, в д.е. мы считали:

или в тысячах д.е.:

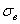
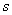
Примечание: на практике часто считают именно через , но для оценки коэффициента вариации всей генеральной совокупности, конечно же, корректнее использовать исправленное стандартное отклонение .

В статистике существует следующий эмпирический ориентир:

– если показатель вариации составляет примерно 30% и меньше, то статистическая совокупность считается однородной. Это означает, что большинство вариант находится недалеко от средней, и найденное значение 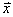хорошо характеризует центральную тенденцию совокупности.

– если показатель вариации составляет существенно больше 30%, то совокупность неоднородна, то есть, значительное количество вариант находятся далеко от 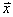, и выборочная средняя плохо характеризует типичную варианту. В таких случаях целесообразно рассмотреть квартили, децили, а иногда и перцентили, которые делят вариационный ряд на части, и для каждого участка рассчитать свои показатели. Но это уже немного дебри статистики.

Другое преимущество относительных показателей – это возможность сравнивать разнородные статистические совокупности. Например, множество слонов и множество хомячков. Совершенно понятно, что дисперсия веса слонов по отношению к дисперсии веса хомяков будет просто конской, и их сопоставление не имеет смысла. Но вот анализ коэффициентов вариации веса вполне осмыслен, и может статься, что у слонов он составляет 10%, а у хомячков 40% (пример, конечно, условный). Это говорит о сбалансированном питании и размеренной жизни слонов. А вот хомяки там, то носятся с голодухи по полям, то отъедаются и спят в норах, и поэтому среди них есть много худощавых и много упитанных особей 🙂

Кроме коэффициента вариации, существуют и другие относительные показатели, но в реальных студенческих работах они почти не встречаются, и поэтому я не буду их рассматривать в рамках данного курса.

И сейчас, конечно же, задачки для самостоятельного решения:

Пример 17, на отработку терминов и формул:

а) Стандартное отклонение выборочной совокупности равно 5, а средний квадрат её вариант – 250. Найти выборочную среднюю.

б) Определите среднее квадратическое отклонение, если известно, что средняя равна 260, а коэффициент вариации составляет 30%.

и Пример 18, творческий:

Производство стальных труб на предприятии (тонн) в 1-м полугодии составило:

Определить:
– среднемесячный объем производства;
– среднее квадратическое отклонение;
– коэффициент вариации.

Сделать краткие содержательные выводы. – Да, это тоже типичный пункт статистической задачи!

Обратите внимание, что здесь не понятно, выборочной ли считать эту совокупность или генеральной. И в таких случаях лучше не заниматься домыслами, просто используем обозначения без подстрочных индексов.

Вообще, задачи на экономическую и промышленную тематику – самые популярные в статистике, и в моей коллекции их сотни. Но все они до ужаса однотипны, и поэтому я предлагаю их в терапевтической дозировке 🙂

Выполнить расчёты в Экселе – числа уже там, ну а инструкцию я на этот раз не привёл, поскольку люди вы уже опытные.

Краткое решение и ответ в конце урока, который подошёл к концу.

Следующее занятие не за горами, а уже за кочкой:

Пример 17. Решение:

а) Используем формулу 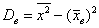. По условию, , . Таким образом:

б) Используем формулу . По условию, , . Таким образом:

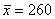
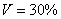
Ответ: а) 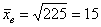, б)

Пример 18. Решение: вычислим сумму вариант и сумму их квадратов: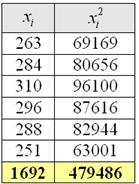

Найдём среднюю:
тонны – среднемесячный объем производства за полугодие.
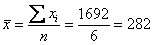
Дисперсию вычислим по формуле: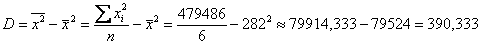

Среднее квадратическое отклонение:
тонн.
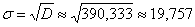
Коэффициент вариации:

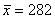
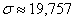
Ответ: тонны, тонн,

Краткие выводы: за первое полугодие среднемесячный объём производства труб составил тонны. Низкие показатели вариации говорят о стабильной ситуации на производстве.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник