Что такое озм в физике определение
Что такое озм в физике определение
осенне-зимний максимум нагрузки
осколочная заградительная мина
Словарь: Словарь сокращений и аббревиатур армии и спецслужб. Сост. А. А. Щелоков. — М.: ООО «Издательство АСТ», ЗАО «Издательский дом Гелеос», 2003. — 318 с.
опытный завод машиностроения
Словарь: С. Фадеев. Словарь сокращений современного русского языка. — С.-Пб.: Политехника, 1997. — 527 с.
отделение землеройных машин
основная запись материала
Смотреть что такое «ОЗМ» в других словарях:
ОЗМ-3 — советская противопехотная выпрыгивающая осколочная мина кругового поражения. Была разработана в СССР. Свое происхождение ведет от немецкой выпрыгивающей мины SMI 35 времен Второй мировой войны. При срабатывании взрывателя огонь пламени… … Википедия
ОЗМ-4 — ОЗМ 4 противопехотная выпрыгивающая осколочная мина кругового поражения. Была разработана в СССР. Свое происхождение ведет от немецкой выпрыгивающей мины SMI 44 времён Второй Мировой войны. При срабатывании взрывателя огонь пламени… … Википедия
ОЗМ-72 — ОЗМ 72 противопехотная выпрыгивающая осколочная мина кругового поражения Была разработана в СССР. Расшифровывается как осколочная заградительная мина. Своё происхождение ведёт от немецкой выпрыгивающей мины SMI 44 времён Второй… … Википедия
ОЗМ — См. Диагностическое и статистическое руководство. Психология. А Я. Словарь справочник / Пер. с англ. К. С. Ткаченко. М.: ФАИР ПРЕСС. Майк Кордуэлл. 2000 … Большая психологическая энциклопедия
ОЗМ — опытный завод машиностроения осколочно заградительная мина отделение землеройных машин … Словарь сокращений русского языка
Выпрыгивающая мина — Диаграмма детонации выпрыгивающей мины Выпрыгивающая мина выпрыгивающая осколочная мина кругового поражения. Является разновидностью противопехотной мины. Свое происхождение ведет от немецкой выпрыгивающей мины Schrapnell Mine времен Первой … Википедия
Шрапнель — У этого термина существуют и другие значения, см. Шрапнель (значения). Устройство диафрагменной шрапнели … Википедия
Африканская партия независимости Гвинеи и Островов Кабо-Верде — (Partido africano da independência da Guine e Cabo Verde PAIGC, ПАИГК), революционно демократическая партия Республики Гвинея Бисау (РГБ). Основана в сентябре 1956 (до 1960 называлась Африканская партия независимости). Основатель и… … Энциклопедический справочник «Африка»
Что такое озм в физике. Физические основы механики
осенне-зимний максимум нагрузки
осколочная заградительная мина
опытный завод машиностроения
отделение землеройных машин
основная запись материала
Смотреть что такое «ОЗМ» в других словарях:
Лекция № 1
Физика в познании вещества,
поля, пространства и времени.
Каленский Александр
Васильевич
Д.ф-м.н., профессор ХТТи
ХМ
Физика и Химия
Физика – наука о природе
Физика
Задачи
Основные методы научного познания
Границы применимости физических законов и теорий
Современная физическая картина мира
10. Кинематика
11. физическая модель
12. Пример
13. Физические величины
14. Физические величины
15. Размерность физической величины
16. Определение размерности
17. Пример
18. Что надо знать?
19. Основные понятия кинематики
20. Определения
21. Материальная точка
22. Система отсчета
24. Относительность движения
26. Определения
27. Отличия пути и перемещения
28. Решите задачи
29. Решить задачу
30. Решить задачу
31. Решение:
32. Задача
33. Что надо знать?
Шпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
Для начала картинка, которую можно распечатать в компактном виде.
Молекулярная физика и термодинамика
Электростатика и электродинамика – формулы по физике
Физика атомного ядра
Преподавание физики в российской школе традиционно ведётся аудиовизуальным методом: учитель объясняет материал и показывает опыты, или учащиеся под руководством учителя сами прокладывают себе дорогу к знаниям с помощью опытов, учебника, дискуссий.
1. Понятие механического движения. ОЗМ
Располагаем произвольно на столе предметы из пенала (ластик, ручка, точилка, циркуль. ) и запоминаем их расположение. Просим соседа переложить один предмет и описываем изменение его положения. Передвигаем тело в прежнее положение. А теперь вопросы: Что произошло с телом? (Тело двигалось, перемещалось.) Как можно описать изменение положения тела? (Относительно других тел.). Что ещё менялось, кроме положения тела? (Время.)
Повторяем опыт с другим телом самостоятельно и проговариваем (по предложению учителя) изменение состояния тела. Мы решаем ОЗМ!
Опыт полезно делать на пару с соседом по парте, выбирая разные системы отсчёта и сравнивая результаты.
3. Виды движения. Материальная точка. По заданию учителя берём лист бумаги и приводим его в движение – поступательное равномерное, вращательное равномерное, поступательное неравномерное и т.д. При изучении равномерного и равноускоренного движения бывает очень интересно его моделировать, двигая пенал, ластик, авторучку в разных направлениях – по горизонтали и по вертикали – с разными скоростями, равномерно и с разгоном или торможением. Ещё лучше, если движение сопровождать соответствующим звуком, как это делают малыши, играя в машинки. С помощью метронома оцениваем и скорость равномерного движения тела по столу, и среднюю скорость неравномерного движения различных тел, а затем сравниваем свои результаты с результатами разных учеников.
5. Относительность движения. При изучении относительности движения и закона сложения скоростей Галилея используем в качестве неподвижной системы отсчёта стол, в качестве подвижной системы отсчёта – учебник и ластик на нём (как движущееся тело). Моделируем: 1) ситуацию удвоения скорости ластика относительно стола, двигая учебник в том же направлении, что и ластик; 2) ситуацию покоя ластика относительно стола, двигая ластик в одну сторону, а учебник – в противоположную; 3) «переплывание» ластиком «реки» (стола) для разных направлений течения реки (движения учебника) при сложении взаимно перпендикулярных скоростей.
6. Свободное падение. Традиционный демонстрационный опыт – сравнение времени падения расправленного листа бумаги (сложенного, а затем скомканного – лучше брать тонкую и мягкую бумагу) гораздо полезнее ставить как фронтальный. Учащиеся лучше понимают, что скорость падения определяется формой тела (сопротивлением воздуха), а не его массой. От анализа этого самостоятельного опыта легче перейти к опытам Галилея.
7. Время свободного падения. Хорошо известен, но всегда эффективен опыт по определению времени реакции ученика: один из сидящей за партой пары отпускает линейку (длиной приблизительно 30 см) нулевым делением вниз, второй, дождавшись старта, старается поймать линейку указательным и большим пальцами. По показаниям l места захвата рассчитывают время реакции каждого ученика (t = ), обсуждают результаты и точность опыта.
9. Второй закон Ньютона. 1) Рассматриваем изменение скорости железных шариков разной массы под действием полосового магнита (движение по прямой) и делаем вывод о влиянии массы на ускорение тела (измеряем скорость). 2) Проводим аналогичный опыт, но с двумя магнитами, сложенными параллельно, одноимёнными полюсами в одну сторону. Делаем вывод о влиянии величины магнитной силы на ускорение и изменение скорости. 3) Прокатываем шарик перпендикулярно полосовому магниту и наблюдаем переход прямолинейной траектории в криволинейную. Делаем вывод об изменении вектора скорости и в этом случае.
10. Третий закон Ньютона. При изучении третьего закона Ньютона можно использовать ладони самих учащихся: предлагаем им сложить ладони перед грудью и попробовать сдвинуть одной ладонью (а не плечами!) другую. Учащиеся сразу понимают, что взаимодействие – одно, сил – две, взаимодействующих тел – два, силы равны и противоположно направлены.
Радостные детские лица, на которых отражается ощущение понимания сути законов и явлений, пропущенных не только через аналитическое мышление, ассоциативный ряд приведённых примеров, но и через телесные ощущения, – лучшая награда за время и усилия, потраченные на организацию, проведение и совместный анализ этих несложных опытов.
Закон cохранения импульса
9 класс, 10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела
→ →
p = mv
p — импульс тела [кг*м/с]
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса
Векторная сумма импульсов тел в замкнутой системе постоянна
А выглядит — вот так:
Закон сохранения импульса
→ → →
p1 + p2 + … + pn = const
p — импульс тела [кг*м/с]
Простая задачка
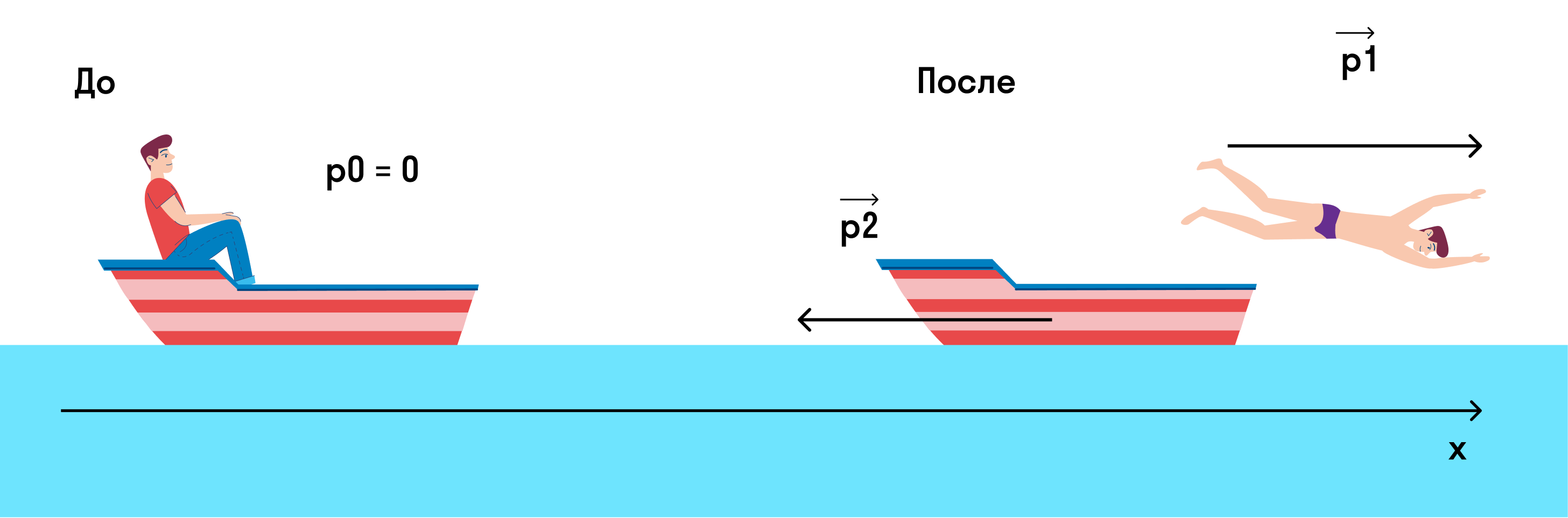
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
p0 — это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
p1 — это импульс мальчика после прыжка,
p2 — это импульс лодки после прыжка.
Изобразим на рисунке, что происходило до и после прыжка.
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
0 = p1 — p2
p1 = p2
Подставим формулу импульса.
mV1 = MV2
Выразим скорость лодки V2:
V2 = mV1/M
Подставим значения:
V2 = 45*3/270 = 3/6 = ½ = 0,5 м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
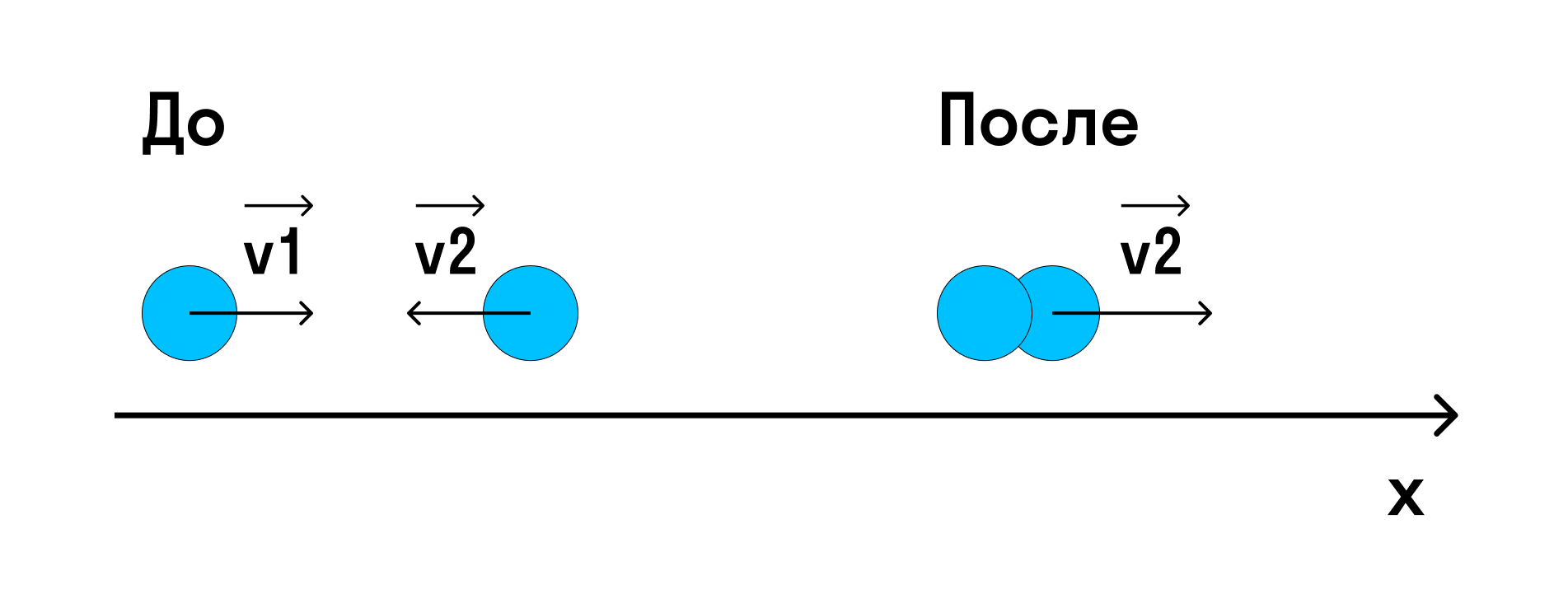
Задачка посложнее
Решение: Для данной системы выполняется закон сохранения импульса:
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
Спроецируем импульсы на ось х:
После неупругого удара получилось одно тело массы m1 + m2, которое движется с искомой скоростью:
m1v1 — mv2 = (m1 + m2) v
Отсюда находим скорость тела, образовавшегося после удара:
v = (m1v1 — mv2)/(m1 + m2)
Переводим массу в килограммы и подставляем значения:
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на значение получившееся значение.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
Применим выражение для ускорения
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
В правой части находится Δv =v —v0 — это разница между конечной и начальной скоростью.
Преобразуем правую часть
Раскрыв скобки, получим
Заменим произведение массы и скорости на импульс:
То есть, вектор Δv⋅m – это вектор Δp.
Тогда второй закон Ньютона в импульсной форме запишем так
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме
Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
Сила F2 называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.
Закон сохранения импульса позволяет оценить скорость ракеты.
mг vг = mр vр,
где mг — это масса горючего,
vг — скорость горючего,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
Скорость ракеты при реактивном движении
vр = mг vг / mр
mг — это масса горючего [кг]
vг — скорость горючего [м/с]
mр — масса ракеты [кг]
v р — скорость ракеты [м/с]
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Что такое озм в физике. Физические основы механики
осенне-зимний максимум нагрузки
осколочная заградительная мина
опытный завод машиностроения
отделение землеройных машин
основная запись материала
Смотреть что такое «ОЗМ» в других словарях:
Лекция № 1
Физика в познании вещества,
поля, пространства и времени.
Каленский Александр
Васильевич
Д.ф-м.н., профессор ХТТи
ХМ
Физика и Химия
Физика – наука о природе
Физика
Задачи
Основные методы научного познания
Границы применимости физических законов и теорий
Современная физическая картина мира
10. Кинематика
11. физическая модель
12. Пример
13. Физические величины
14. Физические величины
15. Размерность физической величины
16. Определение размерности
17. Пример
18. Что надо знать?
19. Основные понятия кинематики
20. Определения
21. Материальная точка
22. Система отсчета
24. Относительность движения
26. Определения
27. Отличия пути и перемещения
28. Решите задачи
29. Решить задачу
30. Решить задачу
31. Решение:
32. Задача
33. Что надо знать?
Шпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
Для начала картинка, которую можно распечатать в компактном виде.
Молекулярная физика и термодинамика
Электростатика и электродинамика – формулы по физике
Физика атомного ядра
Преподавание физики в российской школе традиционно ведётся аудиовизуальным методом: учитель объясняет материал и показывает опыты, или учащиеся под руководством учителя сами прокладывают себе дорогу к знаниям с помощью опытов, учебника, дискуссий.
1. Понятие механического движения. ОЗМ
Располагаем произвольно на столе предметы из пенала (ластик, ручка, точилка, циркуль. ) и запоминаем их расположение. Просим соседа переложить один предмет и описываем изменение его положения. Передвигаем тело в прежнее положение. А теперь вопросы: Что произошло с телом? (Тело двигалось, перемещалось.) Как можно описать изменение положения тела? (Относительно других тел.). Что ещё менялось, кроме положения тела? (Время.)
Повторяем опыт с другим телом самостоятельно и проговариваем (по предложению учителя) изменение состояния тела. Мы решаем ОЗМ!
Опыт полезно делать на пару с соседом по парте, выбирая разные системы отсчёта и сравнивая результаты.
3. Виды движения. Материальная точка. По заданию учителя берём лист бумаги и приводим его в движение – поступательное равномерное, вращательное равномерное, поступательное неравномерное и т.д. При изучении равномерного и равноускоренного движения бывает очень интересно его моделировать, двигая пенал, ластик, авторучку в разных направлениях – по горизонтали и по вертикали – с разными скоростями, равномерно и с разгоном или торможением. Ещё лучше, если движение сопровождать соответствующим звуком, как это делают малыши, играя в машинки. С помощью метронома оцениваем и скорость равномерного движения тела по столу, и среднюю скорость неравномерного движения различных тел, а затем сравниваем свои результаты с результатами разных учеников.
5. Относительность движения. При изучении относительности движения и закона сложения скоростей Галилея используем в качестве неподвижной системы отсчёта стол, в качестве подвижной системы отсчёта – учебник и ластик на нём (как движущееся тело). Моделируем: 1) ситуацию удвоения скорости ластика относительно стола, двигая учебник в том же направлении, что и ластик; 2) ситуацию покоя ластика относительно стола, двигая ластик в одну сторону, а учебник – в противоположную; 3) «переплывание» ластиком «реки» (стола) для разных направлений течения реки (движения учебника) при сложении взаимно перпендикулярных скоростей.
6. Свободное падение. Традиционный демонстрационный опыт – сравнение времени падения расправленного листа бумаги (сложенного, а затем скомканного – лучше брать тонкую и мягкую бумагу) гораздо полезнее ставить как фронтальный. Учащиеся лучше понимают, что скорость падения определяется формой тела (сопротивлением воздуха), а не его массой. От анализа этого самостоятельного опыта легче перейти к опытам Галилея.
7. Время свободного падения. Хорошо известен, но всегда эффективен опыт по определению времени реакции ученика: один из сидящей за партой пары отпускает линейку (длиной приблизительно 30 см) нулевым делением вниз, второй, дождавшись старта, старается поймать линейку указательным и большим пальцами. По показаниям l места захвата рассчитывают время реакции каждого ученика (t = ), обсуждают результаты и точность опыта.
9. Второй закон Ньютона. 1) Рассматриваем изменение скорости железных шариков разной массы под действием полосового магнита (движение по прямой) и делаем вывод о влиянии массы на ускорение тела (измеряем скорость). 2) Проводим аналогичный опыт, но с двумя магнитами, сложенными параллельно, одноимёнными полюсами в одну сторону. Делаем вывод о влиянии величины магнитной силы на ускорение и изменение скорости. 3) Прокатываем шарик перпендикулярно полосовому магниту и наблюдаем переход прямолинейной траектории в криволинейную. Делаем вывод об изменении вектора скорости и в этом случае.
10. Третий закон Ньютона. При изучении третьего закона Ньютона можно использовать ладони самих учащихся: предлагаем им сложить ладони перед грудью и попробовать сдвинуть одной ладонью (а не плечами!) другую. Учащиеся сразу понимают, что взаимодействие – одно, сил – две, взаимодействующих тел – два, силы равны и противоположно направлены.
Радостные детские лица, на которых отражается ощущение понимания сути законов и явлений, пропущенных не только через аналитическое мышление, ассоциативный ряд приведённых примеров, но и через телесные ощущения, – лучшая награда за время и усилия, потраченные на организацию, проведение и совместный анализ этих несложных опытов.
Формирование понятийного аппарата по физике у учащихся общеобразовательных школ
Разделы: Физика
Будучи школьником, уже изучавшим физику, меня начали интересовать вопросы: “Зачем ввели новое понятие? Почему понятие ввели именно такое, а не другое? Можно ли введённое понятие заменить другим понятием?” Этот вопрос меня интересовал и в институте, но к окончанию института я не имел никаких вразумительных ответов по данному вопросу. Подобные вопросы задавали и некоторые мои ученики. Дальнейшая педагогическая практика показала, что одной из отличительных особенностей наиболее успешных учеников при применении знаний оказалось владение ими понятиями, их содержательное использование как инструмента анализа и синтеза в ситуациях, требующих разрешения. Одним из компонентов компетентного специалиста для меня стало владение им понятийным аппаратом.
В КОНЦЕПЦИИ модернизации российского образования на период до 2010 года говорится, что базовое звено образования – общеобразовательная школа, модернизация которой предполагает ориентацию образования не только на усвоение обучающимися определённой суммы знаний, но и на развитие его личности, его познавательных и созидательных способностей. Также в этом документе отмечается, что ученик должен приобрести опыт самостоятельной деятельности.
Очевидно, что одним из путей решения поставленных задач является вовлечение учащегося в исследовательскую деятельность.
Если встать на позицию исследовательской деятельности, то одними из её продуктов являются понятия, понятийный аппарат науки. В последнее время в нормативных документах по контролю за качеством подготовки учащихся стало больше уделяться вниманию контролю за понятийным аппаратом учеников. Например, в сборнике “Оценка качества подготовки выпускников основной школы”, выпущенном Министерством образования Российской Федерации издательством “ДРОФА” в 2000 году говорится, что учащийся должен владеть основными понятиями, давать определения физических величин. Описывать физические явления и процессы, что без владения понятийным аппаратом практически невозможно.
Понятно, что это совсем другой уровень требований, и это правильно.
Однако, несмотря на повышение внимания в руководящих документах на усиление внимания к понятиям, в методической литературе и практике работы учителей этот вопрос не нашёл должного отражения. Мало того, новые учебники по физике ничем не отличаются от старых учебников. В них просто даются определения понятий, никаких изменений в технологии формирования смыслов понятий и их понимания не произошло! В школьных задачниках и учебниках задания направленные на проверку и коррекцию понятийного аппарата практически отсутствуют. От качества сформированного понятийного аппарата во многом зависит качество подготовки выпускника, успех в его профессиональной деятельности. Понятия являются составной частью знаний и принимают самое непосредственное участие в применении знаний и выработке навыков.
Таким образом, возникает противоречие между требованиями федерального компонента государственного стандарта по физике к понятийному аппарату, технологиями формирования понятий и их контролю в методической литературе, содержанием школьных учебников и практикой работы учителей.
Вопросами формирования понятий в эксперименте и в школьном обучении занимались психологи: Б.Г. Ананьев, Л.С. Выгодский, Г.С. Костюк, Н.А. Менчинская, Р.Г. Натадзе, Л.С. Сахаров, Д.Н. Узнадзе и другие.
Как совершенно справедливо отметил П.Я. Гальперин, что процесс формирования понятий в школьном обучении, “в основном, происходит стихийно, т.е. с очень плохим управлением и подавлением многих научных и случайных причин”.
Л.С. Выгодский отмечает, что “ только при возникновении известной потребности, надобности в понятии, только в процессе какой-то осмысленной целесообразной деятельности, направленной на достижение известной цели или решения определённой задачи, может возникнуть и оформиться понятие”.
Один из новых принципов построения учебных предметов, выдвинутых В.В. Давыдовым касается и понятий. Он считает, что “все понятия, конституирующие данный учебный предмет или его основные разделы, должны усваиваться детьми путём рассмотрения предметно-материальных условий их происхождения, благодаря которым они становятся необходимыми (иными словами, понятия не даются как “готовое знание”)”.
В психологии существуют различные методики формирования понятий. Наиболее полно и качественно, с нашей точки зрения, формирует понятийный аппарат у учащихся технология развивающего обучения (РО) Эльконина-Давыдова. Решая систему учебных задач, учащийся, кроме всего прочего, формирует и свой понятийный аппарат. Однако мы не имеем методических рекомендаций для учителя и учебной литературы для ученика, где была бы реализована эта идея для преподавания физики. В данной работе мы постараемся дать свои варианты формирования понятий в системе РО Эльконина-Давыдова.
Второй трудностью учителя в реализации этой концепции является “переделывание” психологии и деятельности ученика, который до изучения физики не учился в системе РО. Ученик в лучшем случае воспроизводил теоретический материал учебника, как правило, без понимания смыслов и выполнял по внешним признакам действия при решении задач. Необходимо вселить уверенность в сознание ученика в возможность решать учебные задачи, осваивать теоретический материал на высоком теоретическом уровне сложности.
Третьей трудностью учителя является научение ученика грамотно выстраивать коммуникационное взаимодействие с участниками учебного процесса в процессе решения учебных задач.
Следует отметить специальную работу учителя и учеников по применению полученных знаний. Это отдельный очень интересный вопрос и его мы специально рассматривать не будем.
Иногда у учащихся вызывает затруднение выделить момент времени, в который они фиксировали местоположение тела. Снять это затруднение может подсказка сделанная учителем в неявном виде. Умение использовать учеником подсказку в неявном виде развивает его мышление, укрепляет его уверенность в своих силах. Можно напомнить им как в детстве их искали родители, что им говорили соседи о вашем местоположении. Видели пять минут назад … Понятно, что нам нужен прибор для измерения времени.
Теперь выявленные закономерности фиксируются в понятии система отсчёта (СО). Становится понятным, что система отсчёта “жила” на бытовом уровне без осознания большинством людей, что она есть и нужна человеку.
Таким образом, чтобы решать ОЗМ, необходимо выбрать СО. Какие задачи, вопросы возникают у учащихся после этого урока, куда эти задачи поведут класс дальше в вопросе изучения механики? Это опять важнейший момент в технологии, так как, в конечном счёте, ученик должен научиться сам ставить перед собой учебные задачи и их решать. Тогда обучение в классе переходит в самообучение, саморазвитие. Запускается природный механизм познания и пытливости ума человеческого. Это одно из достоинств этой технологии.
На первый взгляд всё хорошо. Понятие СО сформулировано, учащиеся (пусть и не все) принимали в этом участие. Но кто что взял для своей деятельности из этого продукта в коллективно-распределительной деятельности класса на уроке? Кто чем овладел, кто что понял, кто понял неправильно, как это понятие использовать, применять? Теперь нужна система заданий и долгая кропотливая работа для получения ответа учителем на поставленные выше вопросы. Это вся работа остаётся за кадром нашей работы. Это отдельная тема и её мы касаться не будем.
Таким образом, была создана ситуация, как вариант, где виден вариант рождение понятия СО.
Цель учителя – создать ситуацию, в которой у учащихся родится понятие механическое движение и покой. Вариант УЗ. Решить ОЗМ в различные моменты времени в СО связанной с Землёй для тел: ваш дом, любой автомобиль и Луна и выявить в полученных описаниях закономерности.
Как правило, эту УЗ удаётся всегда решить на уроке. Учащиеся говорят, что дом своё местоположение относительно Земли не меняет, а Луна всё время изменяет своё местоположение. Таким образом, получается две группы тел: не изменяющие своего местоположения и изменяющие местоположение с течением времени в нашей СО. Автомобиль переходит из одной группы в другую и не занимает постоянного места в группе. Что же делать дальше? Фиксировать полученные закономерности. Дать название этим группам с указанием признаков, по которым мы тела можем отнести к той или иной группе. Рождение понятия заканчивается формулированием его определения. Изменение местоположения тела в пространстве относительно других тел с течением времени называется механическим движением. Покой, это такое состояние тела, при котором его местоположение не изменяется с течением времени.
Человек сел в автобус и едет из одной части города в другую. Движется он или покоится? Покоится относительно автобуса, но движется относительно Земли. Становится ясным, что понятия механического движения и покоя понятия относительные. Информируя о движении тела, мы должны информировать и о СО, в которой это происходит. Результат наблюдаемого явления зависит и от СО. Наблюдая за одним телом в один и тот же промежуток времени мы можем получить различные результаты в зависимости от СО.
Понятно, что для покоящихся тел в нашей СО ОЗМ решена, а для движущихся тел её надо решать. Решать ОЗМ мы можем двумя способами – опытным путём и теоретически.
Решим ОЗМ теоретически. Для этого мы сообщаем названия существующих способов решения ОЗМ – естественный (траекторный), векторный и координатный. Что будем делать дальше? Как правило, учащиеся начинают анализировать названия способов. Начинается поиск ключевого слова и соотнесения его с ОЗМ. Траектория – это линия, вдоль которой движется тело (след оставленный телом). Чертим на доске и в тетради произвольную траекторию в выбранной СО. Чем нам помогает траектория в решении ОЗМ? Траектория ограничивает зону поиска тела, понятно, что тело надо искать на этой траектории. Что для этого нужно дополнительно? Если у учащегося сформировано из математики понятие длины, он им владеет в своей деятельности, его сознательно использовал раньше, то ответ очевиден – надо знать длину линии, которую прошло тело к данному моменту времени (путь пройденный телом). Мы рекомендуем учащимся путь обозначать буквой l, чтобы не путать с модулем вектора перемещения S, поскольку l=S только при определённых условиях, когда движение прямолинейное в одном направлении. Естественно, возникает вопрос – откуда взять путь? Путь и время связаны между собой. Это мы видим из анализа собственного движения, но как показать эту связь аналитически, как найти l=f(t)?
Анализ предыдущей деятельности показывает, что путь и время это разнородные величины и для их связи аналитически ввели специальную величину – скорость механического движения.
Но вернёмся к понятию средней путевой скорости. Средней путевой скоростью называется физическая величина, показывающая как быстро изменяется путь пройденный телом за какой-то промежуток времени, и рассчитываема Vср,l=l/t. Следует отметить, что средняя скорость всегда относится к участку пути или к промежутку времени. Применяя любую физическую величину, нужно чётко выделять к какому физическому телу она применяется. Необходимо также выделять последовательность действий, которые нужно произвести, чтобы найти физическую величину, цель этих действий и их основания. Причём всё это идет в комплексе и должно идти от смыслов, заложенных в этой физической величине. В понятии в свёрнутом виде всегда находится ситуация с требованием (задача), способ её решения, идея решения и необходимость введения этой физической величины в контексте ведущей, главной решаемой задачи. Отсутствие одного из компонентов резко снижает качество выполнения операций, превращая их в механический набор действий, что резко снижает качество подготовки ученика.
Теперь мы имеем ответ на нашу УЗ – l=Vср,l•t. Естественно возникает вопрос, что будем делать дальше? Проверять полученную закономерность на практике. Можно дать возможность учащимся самим составить задание для проверки на практике выявленной закономерности. Можно предложить искать местонахождение группы туристов по карте с их маршрутом следования, если известна средняя путевая скорость за всё время движения. Опираясь на свой жизненный опыт, учащиеся говорят о расхождениях теории и практики. Причину они видят в изменении скорости движения туристов с течением времени. Мы решили ОЗМ траекторным способом, но такое решение неточное. Если неточности (погрешности) нас устраивают, то мы используем этот метод, если нет, то ищем другой путь решения ОЗМ. Думаем.
Работая в группе, учащиеся, как правило, приходят к выводу, что если величина скорости не будет изменяться с течением времени, то l=v•t. И наши теоретические расчёты будут полностью подтверждаться практикой. Но может возникнуть у учащихся вопрос в этой ситуации: “О какой скорости идёт речь?”. Если этого вопроса не возникает, то можно спросить какие физические ве-
личины измеряет спидометр в автомобиле? Как правило, работа в группах с последующим обсуждением, приводит нас к выводу, что это скорость тела в данный момент времени, или в данной точки траектории. Но в данном тексте нет теоретического способа нахождения этой величины. Надо этот способ найти. Опять получается УЗ. Причём, как правило, всё больше и больше учащихся участвуют в составлении УЗ. Это очень важный показатель для учителя. Он показывает ход развития мышления учащихся, понимание ими изучаемого материала, степень участия в создании общегруппового продукта и многое другое.
При поиске способа определения величины мгновенной скорости учащиеся в качестве “исходного материала” берут определение средней путевой скорости и уменьшая промежуток времени приходят по сути дела к понятию производной. УЗ и способ её решения в конечном счёте оформляется в определении. Происходит сворачивание информации, что очень важно для её применения. В определении ученик видит ситуацию, требование и способ исполнения этого требования, и это значительно облегчает выполнение действий при нахождении мгновенной скорости, т.к. за каждым действием есть цель действия и основание действия, реализуемая идея, есть что реализовывать по содержанию. На наш взгляд, это один из принципиальных вопросов технологии, когда выявленная закономерность проживает в сознании ученика развитие от зарождения УЗ до её решения, а затем и сворачивания информации в виде определения понятия или закона с последующим применением этого понятия. При таком пути развития знания, применение, использование знаний значительно облегчается для ученика. Качество знаний учащихся значительно повышается. Технология работы с текстом и технология решения задач, в связи с этим, принципиально иная! Это очень важный вопрос технологии.
Ряд понятий, относящихся к механическому движению и покою у нас родилось, но этого мало. Необходимо следить за жизнью и развитием этих понятий, как в сознании ученика, так и в теории физики. Необходима специальная работа над развитием этого понятия. Выражение смыслов, заложенных в понятии через другие понятия, применение этого понятия к другим ситуациям и расширение его толкования. Когда речь заходит о вращении тела, что в этом случае будет являться механическим движением? А какой будет ОЗМ при вращении тела?
Как иначе сказать в траекторном способе решения ОЗМ, что тело движется? Как выразить этот смысл через другие понятия? Решая эти и подобные им вопросы, мы проверяем понимание учеником изучаемого материала, умение его использовать в новой для него ситуации. Понятия содержательно связываются между собой, становятся системой понятий, единым инструментарием для анализа задач и способом написания текста решения. Необходимы специальные задания для проведения контрольно-оценочной деятельности (КОД) отвечающие за корректировку и контроль за понятийным аппаратом.
Решать УЗ полезно учащимся и дома. Причём можно пользоваться любой литературой: учебниками, справочниками, энциклопедиями … Все это заставляет учащихся активно решать УЗ. Работая с учебником, в конечном счёте, ученики видят между строчек систему учебных задач, способы их решения, сами решения и ответы, сформулированные автором. Да это происходит не сразу, в каждом классе по-разному, но это уже другие ученики. Ученики думающие, обосновывающие свои действия, способные содержательно возражать и спрашивать, активно дополнять и исправлять тексты. Они чётко осознают необходимость введения понятия в контексте основной задачи, в явном виде говорят о способе решения задачи. Понятия становятся их инструментом при анализе и решении задач.
Если больше никто из учителей не работает в классе в этой технологии, то одним из способов проверки степенью овладения этой технологией учеником является умение переноса её на другие предметы. Если это происходит, то развитие ученика идёт по максимально благоприятному сценарию. В конечном счёте, учитель для такого ученика должен выполнять функцию консультанта, проводить КОД и участвовать в рефлексии процессов и результатов КОД.