Что такое парабола в геометрии

Что такое Парабола

Определение Параболы

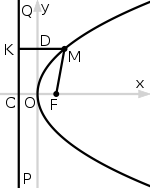
Парабола (от греч. παραβολή — сравнение, приближение, кривая линия) — в геометрии это плоская кривая линия (в форме арки), где каждая из точек M (на рисунке ниже) равноудалена от неподвижной точки F (фокус) и от неподвижной линии DA, называемой директрисой (MF = MA).

Расстояние от фокуса до директрисы называется фокальным параметром параболы и обозначается как p.

В литературе парабола — это аллегория, под которой скрывается важная истина.

Как выглядит парабола, когда меняется фокальный параметр (p)

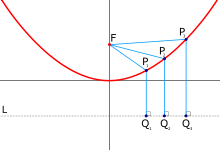
Изменения фокального параметра, когда фокус находится на оси OX:

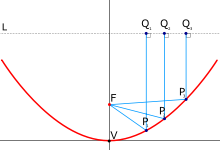
Изменения фокального параметра, когда фокус находится на оси OY:

Квадратичная функция и как построить график параболы

Квадратичная функция выглядит следующим образом:

y = ax² + bx + c, где a≠0

(a — старший коэффициент; b — второй коэффициент; с — свободный член).

Построение графика квадратичной функции

Шаги построения графика

1. Как определить, куда направлены ветви параболы

Т. е. a (старший коэффициент) в данном случае равен 1, b (второй коэффициент) и c (свободный член) оба равны 0.

Ветви параболы будут направлены вверх, когда a > 0.

А в данном случае a = –1 (b = 0, с = 0).

Ветви параболы будут направлены вниз, когда a 0, то у квадратичной параболы будут две точки пересечения с осью ОХ, которые можно найти по этим формулам:

3. Как вычислить координаты вершины параболы

Формулы для их вычисления:

4. Как посчитать точку пересечения параболы с осью OY

Точка пересечения параболы с осью OY имеет координаты (0;c). Так как абсцисса любой точки, лежащей на оси OY, равна нулю.

Чтобы найти точку пересечения параболы с осью OY, нужно всего лишь в вашу формулу вида ax² + bx + c вместо х подставить ноль.

Пример построения графика квадратичной функции

Например, нужно построить график квадратичной функции y = x² − 7x + 10.

1) Если квадратичная функция выглядит как y = ax² + bx + c, получается, в нашем случае: a = 1, b = −7, c = 10.

a = 1, а это a > 0, следовательно ветви параболы будут направлены вверх

2) Определяем нули функции, это значит ax² + bx + c = 0, в нашем случае: x² − 7x + 10 = 0

Ищем дискриминант по формуле: D = b² − 4ac, это D = (−7)² − 4*1*10 = 49 − 40 = 9

Потом вычисляем х1 и х2:

х1 = (−b + ²√D) / 2a = (7 + ²√9) / (2*1) = 5

х2 = (−b − ²√D) / 2а = (7 − ²√9) / (2*1) = 2

3) Вычисляем координаты вершины параболы:

х0 = −b / 2a = 7 / (2*1) = 3,5

y0 = −D / 4а = −9 / (4*1) = −2,25

4) Точка пересечения параболы с осью OY имеет координаты (0;c), следовательно, если c = 10, она пересекает её на (0;10).

Таким образом, получилась парабола такого вида:

Свойства квадратичной функции y = x²

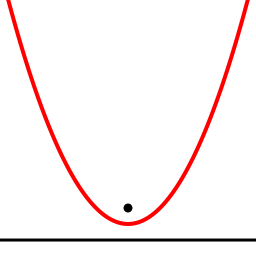
График функции y = x² выглядит следующим образом:

Свойства

1) Область определения функции y = x² — множество всех действительных чисел, т. е. D(y) = R = (−∞; +∞).

2) Множество значений функции — положительная полупрямая: E(y) = [0; +∞).

3) В точке x = 0 (и y = 0) функция принимает минимальные значения (наибольшего значения у функции нет).

Эта точка (с координатами (0;0)) является вершиной параболы; одновременно точка (0;0) является единственной общей точкой параболы с осями координат (начало координат).

4) Функция у = x² чётная, график симметричен относительно оси Оу, т. е. f(−x) = (−x)² = x² = f(x).

5) Функция непрерывна на всей области определения. На (−∞; 0) функция монотонно убывает, а на (0; + ∞) функция монотонно возрастает.

6) Функция у = x² непериодическая.

7) Единственный нуль функции — значение аргумента x = 0.

8) Функция у = x² не имеет асимптот.

9) Функция принимает положительные значения на всех точках параболы, кроме начала координат, т. е. в: (−∞;0) ∪ (0;+∞).

Источник

Парабола

Парабола, её фокус и директриса
Коническое сечение:
Эксцентриситет:
Уравнение:
гипербола · парабола · эллипс · окружность

Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Содержание

Уравнения

0″ border=»0″ /> (или , если поменять местами оси).

Уравнение директрисы : , фокус — , таким образом начало координат — середина отрезка . По определению параболы для любой точки , лежащей на ней выполняется равенство . и , тогда равенство приобретает вид:

.

После возведения в квадрат и некоторых преобразований получается равносильное уравнение .

Квадратное уравнение при также представляет собой параболу и графически изображается той же параболой, что и , но в отличие от последней имеет вершину не в начале координат, а в некоторой точке , координаты которой вычисляются по формулам:

где — дискриминант

Ось её симметрии проходит через вершину параллельно оси ординат, при a>0 (a Расчёт коэффициентов квадратного уравнения

Если для уравнения известны координаты 3-х различных точек его графика , , , то его коэффициенты могут быть найдены так:

Свойства

Связанные определения

Параболы в физическом пространстве

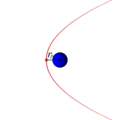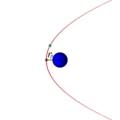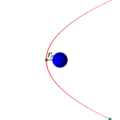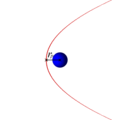
Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости имеют форму параболы (или гиперболы). Эти тела вследствие своей большой скорости не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности аппаратов Вояджер).

При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.

Также параболические зеркала используются в любительских переносных телескопах систем Кассергена, Шмидта — Кассергена, Ньютона, а в фокусе параболы устанавливают вспомогательные зеркала, подающие изображение на окуляр.

При вращении сосуда с жидкостью вокруг вертикальной оси поверхность жидкости в сосуде и вертикальная плоскость пересекаются по параболе.

Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио…), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.

Форма параболы иногда используется в архитектуре для строительства крыш и куполов.

Параболическая орбита и движение спутника по ней (анимация)

Параболические траектории струй воды

Вращающийся сосуд с жидкостью

См. также

Примечания

Литература

Ссылки

Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды)

Конические сечения
Главные типы	Эллипс • Гипербола • Парабола
Вырожденные	Точка • Прямая • Пара прямых
Частный случай эллипса	Окружность
Геометрическое построение	Коническое сечение • Шары Данделена
См. также	Коническая константа
Математика • Геометрия

Полезное

Смотреть что такое «Парабола» в других словарях:

ПАРАБОЛА — (греч. parabole, от parabollo сближаю). 1) иносказание, притча. 2) кривая линия, происходящая от сечения конуса плоскостью, параллельною какой нибудь его производящей. 3) кривая линия, образующаяся при полете бомбы, ядра и т. п. Словарь… … Словарь иностранных слов русского языка

парабола — иносказание, притча (Даль) См. пример … Словарь синонимов

ПАРАБОЛА — (греч. parabole) плоская кривая (2 го порядка). Парабола множество точек М, расстояния которых до данной точки F (фокуса) и до данной прямой D1D2 (директрисы) равны. В надлежащей системе координат уравнение параболы имеет вид: y2=2px, где р=2OF.… … Большой Энциклопедический словарь

ПАРАБОЛА — ПАРАБОЛА, математическая кривая, КОНИЧЕСКОЕ СЕЧЕНИЕ, образуемое точкой, двигающейся таким образом, что ее расстояние до неподвижной точки, фокуса, равно ее расстоянию до неподвижной прямой, директрисы. Парабола образуется при разрезе конуса… … Научно-технический энциклопедический словарь

ПАРАБОЛА — жен., греч. иносказанье, притча. | мат. кривая черта, из числа конических сечений; разрез сахарной головы накось, опостен (параллельно) противной стороне. Парабольные вычисленья. Параболическое реченье, инословие, иноречие, переносное.… … Толковый словарь Даля

ПАРАБОЛА — (1) незамкнутая кривая линия 2 го порядка на плоскости, являющаяся графиком функции у2 = 2рх, где р параметр. Параболу получают при пересечении кругового (см.) плоскостью, не проходящей через его вершину и параллельной одной из его образующих.… … Большая политехническая энциклопедия

ПАРАБОЛА — (от греческого parabole), плоская кривая, расстояния любой точки M которой до данной точки F (фокуса) и до данной прямой D 1D1 (директрисы) равны (MD=MF) … Современная энциклопедия

ПАРАБОЛА — ПАРАБОЛА, параболы, жен. (греч. parabole). 1. Кривая второго порядка, представляющая коническое сечение прямого кругового конуса плоскостью, параллельною одной из образующих (мат.). || Путь, описываемый тяжелым телом (напр. пулей), брошенным под… … Толковый словарь Ушакова

ПАРАБОЛА — ПАРАБОЛА, ы, жен. В математике: состоящая из одной ветви незамкнутая кривая, образующаяся при пересечении конической поверхности плоскостью. | прил. параболический, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

ПАРАБОЛА — «ПАРАБОЛА», Россия, 1992, цв., 30 мин. Документальное эссе. Попытка понять мистическую суть сказаний удмуртов маленького народа в Поволжье. Режиссер: Светлана Стасенко (см. СТАСЕНКО Светлана). Автор сценария: Светлана Стасенко (см. СТАСЕНКО… … Энциклопедия кино

Источник

Парабола

Парабола, её форма, фокус и директриса.

Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^<2>=2px\label
$$
при условии \(p > 0\).

Из уравнения \eqref вытекает, что для всех точек параболы \(x \geq 0\). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.

Форма параболы известна из курса средней школы, где она встречается в качестве графика функции \(y=ax^<2>\). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством \(2p=a^<-1>\).

Фокусом параболы называется точка \(F\) с координатами \((p/2, 0)\) в канонической системе координат.

Директрисой параболы называется прямая с уравнением \(x=-p/2\) в канонической системе координат (\(PQ\) на рис. 8.11).

Рис. 8.11. Парабола.

Свойства параболы.

Расстояние от точки \(M(x, y)\), лежащей на параболе, до фокуса равно
$$
r=x+\frac

<2>.\label
$$

Вычислим квадрат расстояния от точки \(M(x, y)\) до фокуса по координатам этих точек: \(r^<2>=(x-p/2)^<2>+y^<2>\) и подставим сюда \(y^<2>\) из канонического уравнения параболы. Мы получаем
$$
r^<2>=\left(x-\frac

<2>\right)^<2>+2px=\left(x+\frac

<2>\right)^<2>.\nonumber
$$
Отсюда в силу \(x \geq 0\) следует равенство \eqref.

Заметим, что расстояние от точки \(M\) до директрисы также равно
$$
d=x+\frac

<2>.\nonumber
$$

Следовательно, мы можем сделать следующий вывод.

Для того чтобы точка \(M\) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.

Докажем достаточность. Пусть точка \(M(x, y)\) одинаково удалена от фокуса и от директрисы параболы:
$$
\sqrt<\left(x-\frac

<2>\right)^<2>+y^<2>>=x+\frac

<2>.\nonumber
$$

Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы \eqref. Это заканчивает доказательство.

Параболе приписывается эксцентриситет \(\varepsilon=1\). В силу этого соглашения формула
$$
\frac=\varepsilon\nonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.

Уравнение касательной к параболе.

Выведем уравнение касательной к параболе в точке \(M_<0>(x_<0>, y_<0>)\), лежащей на ней. Пусть \(y_ <0>\neq 0\). Через точку \(M_<0>\) проходит график функции \(y=f(x)\), целиком лежащий на параболе. (Это \(y=\sqrt<2px>\) или же \(y=-\sqrt<2px>\), смотря по знаку \(y_<0>\).) Для функции \(f(x)\) выполнено тождество \((f(x))^<2>=2px\), дифференцируя которое имеем \(2f(x)f'(x)=2p\). Подставляя \(x=x_<0>\) и \(f(x_<0>)=y_<0>\), находим \(f'(x_<0>)=p/y_<0>\) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_<0>=\frac

>(x-x_<0>).\nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что \(y_<0>^<2>=2px_<0>\). Теперь уравнение касательной принимает окончательный вид
$$
yy_<0>=p(x+x_<0>).\label
$$

Заметим, что для вершины параболы, которую мы исключили, положив \(y_ <0>\neq 0\), уравнение \eqref превращается в уравнение \(x=0\), то есть в уравнение касательной в вершине. Поэтому уравнение \eqref справедливо для любой точки на параболе.

Касательная к параболе в точке \(M_<0>\) есть биссектриса угла, смежного с углом между отрезком, который соединяет \(M_<0>\) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).

Рассмотрим касательную в точке \(M_<0>(x_<0>, y_<0>)\). Из уравнения \eqref получаем ее направляющий вектор \(\boldsymbol(y_<0>, p)\). Значит, \((\boldsymbol, \boldsymbol_<1>)=y_<0>\) и \(\cos \varphi_<1>=y_<0>/\boldsymbol\). Вектор \(\overrightarrow>\) имеет компоненты \(x_<0>=p/2\) и \(y_<0>\), а потому
$$
(\overrightarrow>, \boldsymbol)=x_<0>y_<0>-\frac

<2>y_<0>+py_<0>=y_<0>(x_<0>+\frac

<2>).\nonumber
$$
Но \(|\overrightarrow>|=x_<0>+p/2\). Следовательно, \(\cos \varphi_<2>=y_<0>/|\boldsymbol|\). Утверждение доказано.

Заметим, что \(|FN|=|FM_<0>|\) (см. рис. 8.12).

Источник