Что такое параллель геометрия
Параллель (геометрия)
Содержание
В евклидовой геометрии
Параллельными (иногда — равнобежными) прямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. В некоторых школьных определениях совпадающие прямые не считаются параллельными, здесь такое определение не рассматривается.
Свойства
В геометрии Лобачевского
Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися.
См. также
Полезное
Смотреть что такое «Параллель (геометрия)» в других словарях:
Параллель (значения) — Параллель: Параллель линия сечения поверхности земного шара плоскостью, параллельной плоскости экватора. Параллель термин, означающий аналогичность в науках, литературоведении и др. Параллель (система) Параллель (геометрия) … Википедия
Геометрия Лобачевского — (1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского Геометрия Лобачевского (гип … Википедия
ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ — геометрия, основанная на тех же основных посылках, что и евклидова геометрия, за исключением аксиомы о параллельных (см. Пятый постулат). В евклидовой геометрии согласно этой аксиоме на плоскости через точку Р, лежащую вне прямой А А, проходит… … Математическая энциклопедия
Лобачевского геометрия — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия
Лобачевского геометрия — геометрическая теория, основанная на тех же основных посылках, что и обычная Евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. Евклидова аксиома о параллельных гласит:… … Большая советская энциклопедия
Плоскость Лобачевского — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия
Успенский, Лев Васильевич — В Википедии есть статьи о других людях с такой фамилией, см. Успенский. Лев Успенский Имя при рождении: Лев Васильевич Успенский Псевдонимы … Википедия
Фалес Милетский — Θαλῆς ὁ Μιλήσιος Θαλῆς ὁ Μιλήσιος … Википедия
Гиппократ Хиосский — В Википедии есть статьи о других людях с именем Гиппократ (значения). Гиппократ Хиосский греч. Ἱπποκράτης Место рождения: остров Хиос Научная сфера … Википедия
Прямая линия. Параллельные прямые. Основные понятия.
Две прямые называются параллельными, если, находясь в одной плоскости, они не пересекаются, сколько бы их ни продолжали. Параллельность прямых на письме обозначают так: AB || СE
Возможность существования таких прямых доказывается теоремой.
Теорема.
Через всякую точку, взятую вне данной прямой, можно провести параллельную этой прямой.
Пусть AB данная прямая и С какая-нибудь точка, взятая вне ее. Требуется доказать, что через С можно провести прямую, параллельную AB. Опустим на AB из точки С перпендикуляр СD и затем проведем СE ^ СD, что возможно. Прямая CE параллельна AB.
Для доказательства допустим противное, т.е., что CE пересекается с AB в некоторой точке M. Тогда из точки M к прямой СD мы имели бы два различных перпендикуляра MD и MС, что невозможно. Значит, CE не может пересечься с AB, т.е. СE параллельна AB.
Следствие.
Аксиома параллельных линий.
Через одну и ту же точку нельзя провести двух различных прямых, параллельных одной и той же прямой.
Так, если прямая СD, проведенная через точку С параллельна прямой AB, то всякая другая прямая СE, проведенная через ту же точку С, не может быть параллельна AB, т.е. она при продолжении пересечется с AB.
Доказательство этой не вполне очевидной истины оказывается невозможным. Ее принимают без доказательства, как необходимое допущение (postulatum).
Следствия.
1. Если прямая (СE) пересекается с одной из параллельных (СВ), то она пересекается и с другой (AB), потому что в противном случае через одну и ту же точку С проходили бы две различные прямые, параллельные AB, что невозможно.
2. Если каждая из двух прямых (A и B) параллельны одной и той же третьей прямой (С), то они параллельны между собой.
Действительно, если предположить, что A и B пересекаются в некоторой точке M, то тогда через эту точку проходили бы две различные прямые, параллельные С, что невозможно.
Теорема.
Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и к другой параллельной.
Перпендикуляр EF, пересекаясь с AB, непременно пересечет и СD. Пусть точка пересечения будет H.
Предположим теперь, что СD не перпендикулярна к EH. Тогда какая-нибудь другая прямая, например HK, будет перпендикулярна к EH и, следовательно через одну и ту же точку H будут проходить две прямые параллельные AB: одна СD, по условию, а другая HK по доказанному раньше. Так как это невозможно, то нельзя допустить, что СВ была не перпендикулярна к EH.
Параллельные прямые, признаки и условия параллельности прямых
В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.
Параллельные прямые: основные сведения
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.
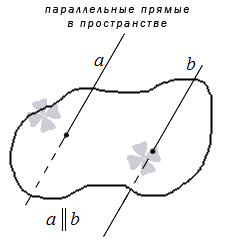
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.
Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.
Сформулируем утверждение, играющее важную роль в изучаемой теме.
Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.
В случае, когда речь идет о пространстве, верна теорема:
Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.
Параллельность прямых: признаки и условия параллельности
Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.
В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.
Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.
Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.
Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.
Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:
Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.
Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:
В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.
Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.
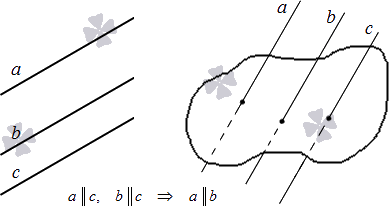
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.
Доказательство признака изучается в программе геометрии 10 класса.
Дадим иллюстрацию указанных теорем:
Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.
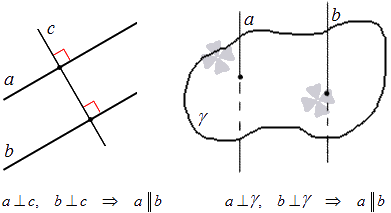
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Сформулируем аналогичное для трехмерного пространства.
В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.
Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.
Параллельность прямых в прямоугольной системе координат
В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.
Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.
Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.
Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.
A 1 = t · A 2 B 1 = t · B 2
Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.
a x = t · b x a y = t · b y
Решение
Запишем уравнение прямой в отрезках в виде общего уравнения:
Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.
Ответ: заданные прямые не параллельны.
Решение
Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.
Следующим шагом определим выполнение условия параллельности заданных прямых.
Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.
Ответ: данные прямые параллельны.
Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.
Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.
a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z
Решение
Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.
Ответ: параллельность заданных прямых доказана.
Содержание
Символ
в Unicode Набор символов, знаки «параллельный» и «непараллельный» имеют кодовые точки U + 2225 (∥) и U + 2226 (∦) соответственно. Кроме того, U + 22D5 (⋕) представляет собой отношение «равно и параллельно». [4]
Евклидов параллелизм
Две линии на плоскости
Условия параллелизма
Учитывая параллельные прямые л и м в Евклидово пространство, следующие свойства эквивалентны:
История
Определение параллельных прямых как пары прямых на плоскости, которые не пересекаются, появляется как Определение 23 в Книге I Элементы Евклида. [6] Альтернативные определения обсуждались другими греками, часто как часть попытки доказать параллельный постулат. Прокл приписывает определение параллельных линий как эквидистантных к Посидоний и цитаты Близнецы в том же духе. Симплициус также упоминает определение Посидония, а также его модификацию философом Аганисом. [6]
В конце девятнадцатого века в Англии «Элементы Евклида» по-прежнему были стандартным учебником в средних школах. Традиционный подход к геометрии был вынужден изменить новые разработки в проективная геометрия и неевклидова геометрия, поэтому в это время было написано несколько новых учебников для преподавания геометрии. Основное различие между этими реформаторскими текстами, как между собой, так и между ними и Евклидом, заключается в трактовке параллельных линий. [7] Эти реформаторские тексты не остались без критики, и один из них, Чарльз Доджсон (a.k.a. Льюис Кэрролл), написал пьесу, Евклид и его современные соперники, в котором эти тексты подвергаются критике. [8]
Одним из первых учебников реформ была книга Джеймса Мориса Уилсона. Элементарная геометрия 1868 г. [9] Уилсон основал свое определение параллельных прямых на примитивное понятие из направление. Согласно с Вильгельм Киллинг [10] идея может быть прослежена до Лейбниц. [11] Уилсон, не определяя направление, поскольку это примитив, использует этот термин в других определениях, таких как шестое определение: «Две прямые линии, которые встречаются друг с другом, имеют разные направления, и разница в их направлениях есть угол между ними.» Уилсон (1868 г., п. 2) В определении 15 он вводит параллельные прямые таким образом; «Прямые линии, то же направление, но не являются частями одной прямой, называются параллельные линии.» Уилсон (1868 г., п. 12) Огастес Де Морган рассмотрел этот текст и объявил его неудачным, в первую очередь на основании этого определения и того, как Вильсон использовал его для доказательства того, что есть параллельные линии. Доджсон также посвящает большую часть своей пьесы (Акт II, Сцена VI § 1) разоблачению трактовки параллелей Уилсоном. Уилсон отредактировал эту концепцию из третьего и более поздних изданий своего текста. [12]
Другие свойства, предложенные другими реформаторами, использованные в качестве замены для определения параллельных линий, оказались не намного лучше. Основная трудность, как указывал Доджсон, заключалась в том, что их использование таким образом требовало добавления в систему дополнительных аксиом. Определение Посидония через равноудаленную линию, изложенное Фрэнсисом Катбертсоном в его тексте 1874 г. Евклидова геометрия страдает от проблемы, заключающейся в том, что точки, которые находятся на фиксированном заданном расстоянии на одной стороне прямой линии, должны быть показаны как прямая линия. Это нельзя доказать, и следует полагать, что это правда. [13] Соответствующие углы, образованные поперечным свойством, используемым В. Д. Кули в его тексте 1860 г., Элементы геометрии, упрощенные и объясненные требует доказательства того факта, что если одна трансверсаль пересекает пару прямых в соответствующих конгруэнтных углах, то все трансверсали должны это делать. Опять же, нужна новая аксиома, чтобы оправдать это утверждение.
строительство
Три указанных выше свойства приводят к трем различным методам построения. [14] параллельных линий.
Содержание
Символ
в Unicode Набор символов, знаки «параллельный» и «непараллельный» имеют кодовые точки U + 2225 (∥) и U + 2226 (∦) соответственно. Кроме того, U + 22D5 (⋕) представляет собой отношение «равно и параллельно». [4]
Евклидов параллелизм
Две линии на плоскости
Условия параллелизма
Учитывая параллельные прямые л и м в Евклидово пространство, следующие свойства эквивалентны:
История
Определение параллельных прямых как пары прямых на плоскости, которые не пересекаются, появляется как Определение 23 в Книге I Элементы Евклида. [6] Альтернативные определения обсуждались другими греками, часто как часть попытки доказать параллельный постулат. Прокл приписывает определение параллельных линий как эквидистантных к Посидоний и цитаты Близнецы в том же духе. Симплициус также упоминает определение Посидония, а также его модификацию философом Аганисом. [6]
В конце девятнадцатого века в Англии «Элементы Евклида» по-прежнему были стандартным учебником в средних школах. Традиционный подход к геометрии был вынужден изменить новые разработки в проективная геометрия и неевклидова геометрия, поэтому в это время было написано несколько новых учебников для преподавания геометрии. Основное различие между этими реформаторскими текстами, как между собой, так и между ними и Евклидом, заключается в трактовке параллельных линий. [7] Эти реформаторские тексты не остались без критики, и один из них, Чарльз Доджсон (a.k.a. Льюис Кэрролл), написал пьесу, Евклид и его современные соперники, в котором эти тексты подвергаются критике. [8]
Одним из первых учебников реформ была книга Джеймса Мориса Уилсона. Элементарная геометрия 1868 г. [9] Уилсон основал свое определение параллельных прямых на примитивное понятие из направление. Согласно с Вильгельм Киллинг [10] идея может быть прослежена до Лейбниц. [11] Уилсон, не определяя направление, поскольку это примитив, использует этот термин в других определениях, таких как шестое определение: «Две прямые линии, которые встречаются друг с другом, имеют разные направления, и разница в их направлениях есть угол между ними.» Уилсон (1868 г., п. 2) В определении 15 он вводит параллельные прямые таким образом; «Прямые линии, то же направление, но не являются частями одной прямой, называются параллельные линии.» Уилсон (1868 г., п. 12) Огастес Де Морган рассмотрел этот текст и объявил его неудачным, в первую очередь на основании этого определения и того, как Вильсон использовал его для доказательства того, что есть параллельные линии. Доджсон также посвящает большую часть своей пьесы (Акт II, Сцена VI § 1) разоблачению трактовки параллелей Уилсоном. Уилсон отредактировал эту концепцию из третьего и более поздних изданий своего текста. [12]
Другие свойства, предложенные другими реформаторами, использованные в качестве замены для определения параллельных линий, оказались не намного лучше. Основная трудность, как указывал Доджсон, заключалась в том, что их использование таким образом требовало добавления в систему дополнительных аксиом. Определение Посидония через равноудаленную линию, изложенное Фрэнсисом Катбертсоном в его тексте 1874 г. Евклидова геометрия страдает от проблемы, заключающейся в том, что точки, которые находятся на фиксированном заданном расстоянии на одной стороне прямой линии, должны быть показаны как прямая линия. Это нельзя доказать, и следует полагать, что это правда. [13] Соответствующие углы, образованные поперечным свойством, используемым В. Д. Кули в его тексте 1860 г., Элементы геометрии, упрощенные и объясненные требует доказательства того факта, что если одна трансверсаль пересекает пару прямых в соответствующих конгруэнтных углах, то все трансверсали должны это делать. Опять же, нужна новая аксиома, чтобы оправдать это утверждение.
строительство
Три указанных выше свойства приводят к трем различным методам построения. [14] параллельных линий.