Что такое параллельная проекция
Что такое параллельная проекция
Лекция № 1. Сведения о проекциях
1. Понятие проекций
Начертательной геометрией называют науку, которая является теоретическим фундаментом черчения. В данной науке изучаются способы изображения на плоскости различных тел и их элементов. Эти изображения позволяют однозначно определить форму и размеры изделия и изготовить его. При работе с чертежами выполняются два вида работ: подготовка чертежей и их чтение.
Чтение чертежа заключается в воспроизведении в уме реальной формы объекта и некоторых его частей с использованием при этом чертежа.
Начертательная геометрия основывается на методе проекций.
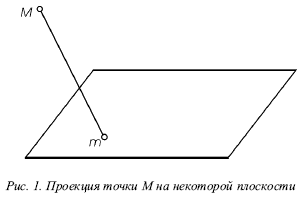
Проекцией точки М на некоторой плоскости называют изображение, которое строится в нижеследующей последовательности (рис. 1).
Через данную точку М необходимо провести прямую, которая не параллельна данной плоскости. Точку пересечения данной прямой и плоскости назовем точкой m. Полученная точка m будет являться проекцией точки М на данную плоскость. Прямую Mm называют проектирующей прямой, а данная плоскость называется плоскостью изображения.
Подобным образом можно получить проекции различных фигур как проекции каждой из его точек. Способ построения определяет вид проекции: центральную или параллельную.
2. Центральная проекция
Представление о центральной проекции можно получить, если изучить изображение, которое дает человеческий глаз.
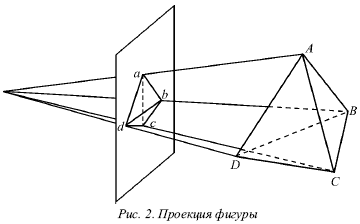
Для построения центральной проекции объекта нужно между глазом и изучаемым предметом поместить прозрачный экран и отметить на нем точки пересечения лучей, которые идут от глаза человека к отдельным точкам предмета. При соединении всех точек на экране получаем изображение (проекцию) фигуры (рис. 2). Эта проекция называется центральной.
Центральная проекция – это проекция, которая образуется с помощью проецирующихся лучей, проходящих через одну точку.
Изображение предметов при помощи центральной проекции встречается очень часто, особенно для предметов, обладающих большими размерами.
3. Параллельная проекция
Параллельная проекция – это такой вид проекции, при построении которого используются параллельные проецирующиеся лучи.
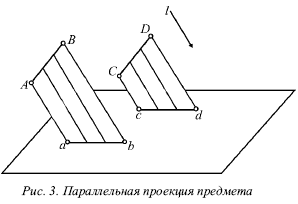
При построении параллельных проекций нужно задать направление проецирующих лучей (рис. 3). На данном примере в качестве направляющего луча выбран луч l. При построении изображений через все точки проводятся прямые, параллельные установленному направлению проецирования, до точки пересечения с плоскостью проекции. Соединяя полученные точки, получаем параллельную проекцию предмета.
Параллельные проекции могут быть ортогональными или косоугольными в зависимости от направления проецирующих лучей.
Проекция называется ортогональной, если проецирующий луч перпендикулярен плоскости.
Проекция называется косоугольной, если угол наклона проецирующих лучей направлен относительно плоскости под углом, отличным от прямого.
Изображение, полученное при помощи параллельной проекции, намного меньше искажено, чем изображение, полученное с помощью центральной проекции.
Параллельное проецирование. Площадь проекции фигуры
В задачах по геометрии успех зависит не только от знания теории, но от качественного чертежа.
С плоскими чертежами все более-менее понятно. А в стереометрии дело обстоит сложнее. Ведь изобразить надо трехмерное тело на плоском чертеже, причем так, чтобы и вы сами, и тот, кто смотрит на ваш чертеж, увидели бы то же самое объемное тело.
Как это сделать?
Конечно, любое изображение объемного тела на плоскости будет условным. Однако существует определенный набор правил. Существует общепринятый способ построения чертежей — параллельное проецирование.
Ты нашел то, что искал? Поделись с друзьями!
Возьмем объемное тело.
Выберем плоскость проекции.
Через каждую точку объемного тела проведем прямые, параллельные друг другу и пересекающие плоскость проекции под каким-либо углом. Каждая из этих прямых пересекает плоскость проекции в какой-либо точке. А все вместе эти точки образуют проекцию объемного тела на плоскость, то есть его плоское изображение.
Как строить проекции объемных тел?
Представьте, что у вас есть каркас объемного тела — призмы, пирамиды или цилиндра. Освещая его параллельным пучком света, получаем изображение — тень на стене или на экране. Заметим, что в разных ракурсах получаются разные изображения, но некоторые закономерности все же присутствуют:
Проекцией отрезка будет отрезок.
Конечно, если отрезок перпендикулярен плоскости проекции — он отобразится в одну точку.
Проекцией круга в общем случае окажется эллипс.
Проекцией прямоугольника — параллелограмм.
Вот как выглядит проекция куба на плоскость:
Здесь передняя и задняя грани параллельны плоскости проекции
Можно сделать по-другому:
Какой бы ракурс мы ни выбрали, проекциями параллельных отрезков на чертеже тоже будут параллельные отрезки. Это один из принципов параллельного проецирования.
Рисуем проекции пирамиды,
Еще раз повторим основной принцип параллельного проецирования. Выбираем плоскость проекции и через каждую точку объемного тела проводим параллельные друг другу прямые. Эти прямые пересекают плоскость проекции под каким-либо углом. Если этот угол равен 90° — речь идет о прямоугольном проецировании. С помощью прямоугольного проецирования строятся чертежи объемных деталей в технике. В этом случае мы говорим о виде сверху, виде спереди и виде сбоку.
Иногда в задачах требуется найти площадь прямоугольной проекции фигуры.
Пусть S — площадь фигуры. Тогда площадь ее прямоугольной проекции равна S cosφ, где φ — угол между плоскостью фигуры и плоскостью проекции.
В следующей статье рассказано, как выбрать наиболее удачный ракурс для построения чертежей в задачах по стереометрии, а также о распространенных ошибках, которые могут помешать решению.
Параллельное проецирование
Очевидно, при таком положении центра проекции и все остальные проецирующие лучи будут также параллельны [SA). Множество всех лучей пространства, параллельных одному лучу, имеющему несобственную точку, образуют связку, центр которой несобственная точка, совпадающая с центром проекции.
В связи с параллельностью проецирующих лучей, рассматриваемый способ проецирования называют параллельным, а полученные с его помощью проекции параллельными проекциями.
Чтобы осуществить параллельное проецирование необходимо иметь аппарат, который полностью определяется положением плоскости проекции α и направлением проецирования s.
Отмеченное ранее свойство центрального проецирования сохраняется и в данном случае. Применительно к параллельному проецированию оно может быть сформулировано:
Каждая точка пространства, при заданном аппарате проецирования, будет иметь одну и только одну параллельную проекцию.
Обратное утверждение, как и в случае центрального проецирования, не имеет места.
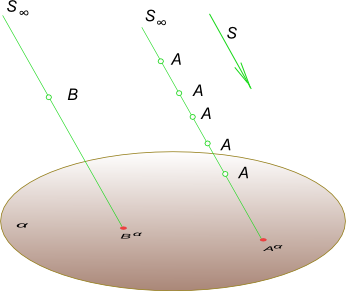
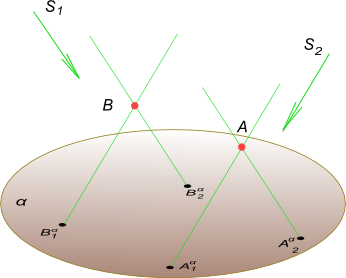
Для определения положения точки в пространстве необходимо иметь две ее параллельные проекции, полученные при двух различных направлениях проецирования.
В этом случае положение точки A определяется пересечением прямых, проведенных через A α 1 и A α 2 параллельно соответствующим направлениям s1 и s2.
На рисунке показано также нахождение положения в пространстве точки B по известным ее параллельным проекциям B α 1 и B α 2.
Параллельная проекция и ее свойства
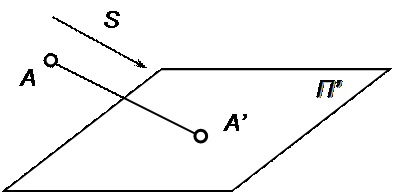
Параллельная проекция является частным случаем центральной, когда центр проекций S удален в бесконечность. При этом задается направление проецирования, параллельно которому проводятся проецирующие лучи. Пусть дана плоскость проекций П’ и точка А (рис.1.4). Для построения проекции точки проведем через точку А проецирующую прямую параллельно заданному направлению проецирования S. Затем определим точку пересечения этой прямой с плоскостью П’ – точку А′, которая называется параллельной проекцией точки А.
Рис.1.4. Параллельная проекция
Параллельная проекция кроме трех свойств центральной проекции обладает еще дополнительными свойствами:
4) проекциями параллельных прямых являются параллельные прямые;
5) отношение проекций отрезков, лежащих на параллельных прямых или на одной и той же прямой, равно отношению самих отрезков;
6) проекция фигуры не меняется при параллельном переносе плоскости проекций.
Эти свойства параллельной проекции обеспечивают более простое построение чертежа, меньше искажающего форму и размеры оригинала по сравнению с центральной проекцией. Так в связи с сохранением параллельности прямых параллельной проекцией параллелограмма является параллелограмм, а трапеции – тоже трапеция, в то время как в центральной проекции эти фигуры проецируются в четырехугольники произвольного вида.
В зависимости от величины угла, образованного направлением проецирования S с плоскостью проекций П’, параллельная проекция подразделяется на ортогональную (прямоугольную), когда угол равен 90°, и косоугольную в остальных случаях.
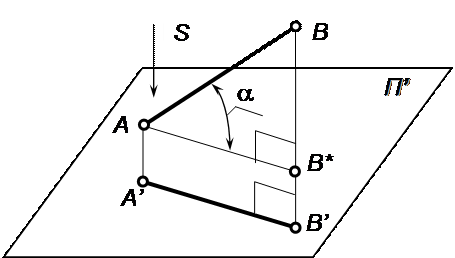
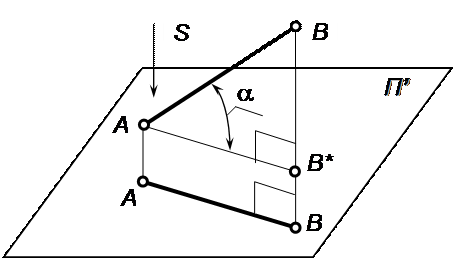
В ортогональной проекции нетрудно установить соотношение между длиной натурального отрезка и длиной его проекции. Если отрезок АВ образует с плоскостью проекций угол a, то, проведя АВ*||А’В’ (рис.1.5), получим из прямоугольного треугольника АВ*В: АВ*=АВсоs(a) или А’В’=АВсоs(a).
Ортогональная проекция получила наибольшее распространение в технических чертежах, т.к. она позволяет наиболее легко судить о размерах изображаемых предметов.
Рассмотренные выше методы проецирования однозначно решают прямую задачу – по данному оригиналу построить его проекционный чертеж. Однако обратная задача – по данному проекционному чертежу воспроизвести (реконструировать) оригинал – не решается однозначно. Эта задача допускает бесчисленное множество решений, т.к. точку А’, например, можно считать проекцией любой точки проецирующей прямой, проходящей через А (рис.1.1, 1.4). Таким образом, рассмотренные проекционные чертежи не обладают свойством обратимости. Для получения обратимых чертежей нужно дополнить проекционный чертеж некоторыми данными. Существуют различные методы такого дополнения. В данном курсе мы будем рассматривать два вида обратимых чертежей, а именно, аксонометрические и комплексные чертежи в ортогональных проекциях.
Дата добавления: 2016-02-02 ; просмотров: 2191 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Параллельная проекция и ее свойства
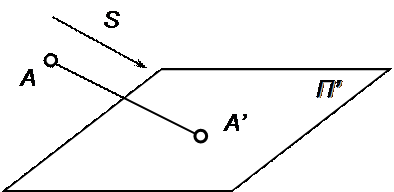
Параллельная проекция является частным случаем центральной, когда центр проекций S удален в бесконечность. При этом задается направление проецирования, параллельно которому проводятся проецирующие лучи. Пусть дана плоскость проекций П’ и точка А (рис.1.4). Для построения проекции точки проведем через точку А проецирующую прямую параллельно заданному направлению проецирования S. Затем определим точку пересечения этой прямой с плоскостью П’ – точку А′, которая называется параллельной проекцией точки А.
Рис.1.4. Параллельная проекция
Параллельная проекция кроме трех свойств центральной проекции обладает еще дополнительными свойствами:
4) проекциями параллельных прямых являются параллельные прямые;
5) отношение проекций отрезков, лежащих на параллельных прямых или на одной и той же прямой, равно отношению самих отрезков;
6) проекция фигуры не меняется при параллельном переносе плоскости проекций.
Эти свойства параллельной проекции обеспечивают более простое построение чертежа, меньше искажающего форму и размеры оригинала по сравнению с центральной проекцией. Так в связи с сохранением параллельности прямых параллельной проекцией параллелограмма является параллелограмм, а трапеции – тоже трапеция, в то время как в центральной проекции эти фигуры проецируются в четырехугольники произвольного вида.
В зависимости от величины угла, образованного направлением проецирования S с плоскостью проекций П’, параллельная проекция подразделяется на ортогональную (прямоугольную), когда угол равен 90°, и косоугольную в остальных случаях.
В ортогональной проекции нетрудно установить соотношение между длиной натурального отрезка и длиной его проекции. Если отрезок АВ образует с плоскостью проекций угол a, то, проведя АВ*||А’В’ (рис.1.5), получим из прямоугольного треугольника АВ*В: АВ*=АВсоs(a) или А’В’=АВсоs(a).
Ортогональная проекция получила наибольшее распространение в технических чертежах, т.к. она позволяет наиболее легко судить о размерах изображаемых предметов.
Рассмотренные выше методы проецирования однозначно решают прямую задачу – по данному оригиналу построить его проекционный чертеж. Однако обратная задача – по данному проекционному чертежу воспроизвести (реконструировать) оригинал – не решается однозначно. Эта задача допускает бесчисленное множество решений, т.к. точку А’, например, можно считать проекцией любой точки проецирующей прямой, проходящей через А (рис.1.1, 1.4). Таким образом, рассмотренные проекционные чертежи не обладают свойством обратимости. Для получения обратимых чертежей нужно дополнить проекционный чертеж некоторыми данными. Существуют различные методы такого дополнения. В данном курсе мы будем рассматривать два вида обратимых чертежей, а именно, аксонометрические и комплексные чертежи в ортогональных проекциях.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет