Что такое параллельно и перпендикулярно
Прямая. Параллельные и перпендикулярные прямые.
теория по математике 📈 планиметрия
Линия, которую изображают на плоскости при помощи линейки, причем, эта линия не должна быть ограничена точкой ни с одной стороны, называют прямой. Другими словами, прямая не имеет ни начала, ни конца.
Обозначения прямой
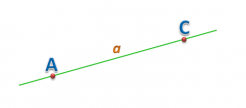
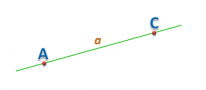
Обычно прямые обозначают прописной латинской буквой или двумя заглавными (если на прямой лежат точки). Рассмотрим это на рисунке. Данную прямую мы можем назвать двумя способами: прямая а; прямая АС.
Рассмотрим теперь две прямые на плоскости. Для них существует два случая расположения: пересекаются и не пересекаются.
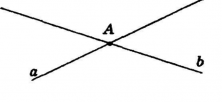
Если две прямые пересекаются, то есть имеют общую точку, то их называют пересекающимися. На рисунке показаны прямые а и b, которые пересекаются в точке A. Запись с помощью символов для данного рисунка выполняют следующим образом: а ∩ b=А, где ∩ — это знак «пересечение».
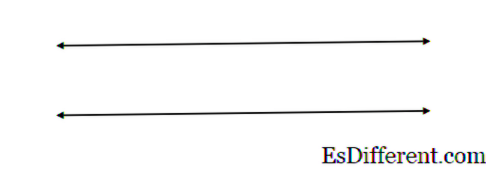
Если две прямые на плоскости не пересекаются, то их называют параллельными прямыми. На рисунке изображены параллельные прямые. Запись осуществляется следующим образом: a | | b, где | | — знак параллельности.
Признаки параллельности прямых
Рассмотрим прямую с, которая пересекает две прямые а и b и образует с ними восемь углов. Такую прямую с называют — секущая. Пары углов, которые образует секущая, также имеют названия. Итак, на данном рисунке изображены эти все прямые и восемь углов.
Аксиома параллельных прямых
Вспомним, что аксиомой принято называть утверждения, не требующие доказательств.
Через любые две точки на плоскости проходит прямая и притом только одна.
Аксиома №2 Через точку, не лежащую на данной прямой, можно провести только одну прямую параллельную данной. 
Следствия из аксиом параллельных прямых
Перпендикулярные прямые
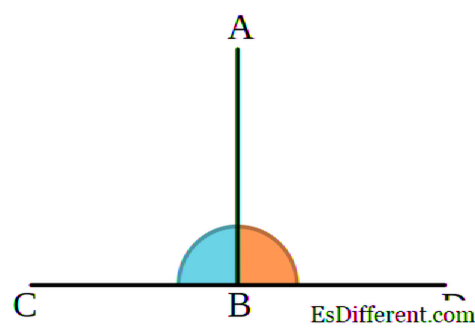
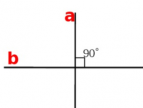
Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
На рисунке показаны такие прямые а и b. Запись с помощью символов можно сделать следующим образом: а ⊥ b, где « ⊥ » — знак перпендикулярности. Заметим, что две прямые, перпендикулярные к третьей, не пересекаются. 
На данном рисунке а ⟂ с, b ⟂ c. Видно, что прямые а и b не пересекаются, то есть они – параллельны.
Разница между параллелью и перпендикуляром
Хотя они обычно связаны с математикой, слова «параллельный» и «перпендикулярный» также применимы к простым вещам, которые мы видим и используем каждый день. На самом деле мы часто
Содержание:
Хотя они обычно связаны с математикой, слова «параллельный» и «перпендикулярный» также применимы к простым вещам, которые мы видим и используем каждый день. На самом деле мы часто видим знаки с надписью «только параллельная парковка» или «только перпендикулярная парковка». Но что они означают? В чем разница между двумя терминами? Читай дальше.
Описания
Слово параллельно происходит от греческого слова параллели что означает «бок о бок». Обычно он используется для описания двух объектов (например, линий), находящихся рядом с одинаковой крутизной и расстоянием между ними. Это означает, что даже если две линии продолжатся, они никогда не соприкоснутся. Поверхности, плоскости, прямые и изогнутые линии могут быть параллельны.
С другой стороны, слово перпендикуляр происходит от латинского термина перпендикулярно что означает «вертикальный». Он относится к чему-либо (например, к линии), лежащей под углом 90 ° от другого объекта. Если, например, две прямые перпендикулярны, это означает, что они пересекаются в одной точке. Тогда это пересечение будет под прямым углом (90º).
Параллельный против перпендикулярного
В чем же тогда разница между «параллельным» и «перпендикулярным»?
Слово «параллельный» относится к двум равноудаленным (имеющим одинаковое расстояние) линиям с одинаковой крутизной, тогда как слово «перпендикулярно» относится к чему-то, что расположено под углом 90 ° от другого объекта. Если мы говорим о прямых, например, точки параллельных линий никогда не будут касаться друг друга, даже если они будут продолжаться и продолжаться, но перпендикулярные линии будут встречаться в одной точке. Это пересечение образует прямой угол.
Перпендикулярные и параллельные прямые
Вы будете перенаправлены на Автор24
Перпендикулярные прямые
Перпендикулярными прямыми называются прямые, которые располагаются на одной плоскости и пересекаются под прямым углом.
Перпендикулярными могут быть не только прямые, но и лучи, и отрезки.
Рассмотрим прямоугольник и квадрат. В них все углы прямые, т.е. равны 90о. Следовательно, соседние стороны каждой и этих геометрических фигур перпендикулярны между собой.
Прямые, которые пересекаются под прямым углом, называются перпендикулярными прямыми.
Отрезки (или лучи), которые лежат на перпендикулярных прямых, называются перпендикулярными отрезками (или лучами).
Готовые работы на аналогичную тему
Параллельные прямые
Параллельными прямыми называются две прямые, которые расположены на плоскости и не пересекаются.
Сформулируем еще и правило:
Через точку, которая не принадлежит на прямой, можно провести только одну прямую, которая будет параллельна исходной.
В жизни параллельные прямые можно встретить, например, на прямых участках железнодорожных путей или прямых участках трамвайных путей.
Довольно часто параллельные прямые встречаются в геометрических фигурах. Например, противоположные стороны квадрата, прямоугольника, параллелограмма, основания трапеции.
Такие геометрические фигуры, как квадрат и прямоугольник, интересны тем, что они содержат и перпендикулярные, и параллельные стороны.
Таким образом, две любые прямые на плоскости могут или пересекаться в одной точке, или не пересекаться.
Отрезки (или лучи), которые лежат на параллельных прямых, называются параллельными отрезками (или лучами).
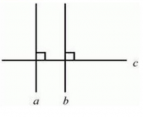
Если представить любые две прямые, которые находятся в одной плоскости, такие, что они перпендикулярны третей прямой, следовательно, эти прямые параллельные между собой.
В прямоугольнике противоположные стороны параллельны и образуют прямые углы с другими сторонами этого прямоугольника.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 20 06 2021
Параллельные и перпендикулярные 2021
Это займет всего лишь минуту, чтобы понять, что линии повсюду. Когда мы ходим, разговариваем и жестикулируем, мы создаем линии, куда бы мы ни пошли. Это захватывающе, потому что везде, где вы смотрите, есть линии. Но часто мы так заняты, так что завернуты в себя, что не можем понять, что они есть. На самом деле они уже были там. Дело не только в том, что построение линии столь же повсеместно, как и использование рук и ног для жестов и ходьбы вокруг, а скорее это явление, которое объединяет все аспекты нашей повседневной деятельности в единую область исследования. Линии бесконечны, и они имеют тенденцию быть прямыми.
В математических терминах линия определяется как прямой путь, который бесконечен. Это множество точек, которые бесконечно расширяются в двух направлениях. Они бесконечно прямые; они продолжаются и продолжаются. Линии могут использоваться разными способами. Мы можем делать прямые линии, мы можем создавать изогнутые линии, и мы можем создавать волнообразные линии. Некоторые линии короткие, некоторые линии длинны, некоторые тонкие, а некоторые толстые. Строка показывает контур фигуры. Один тип линии называется параллельным средством. В геометрии две линии называются параллельными, если они равноудалены и никогда не пересекаются. Если две прямые пересекаются под прямым углом, то они называются перпендикулярными.
Что такое параллель?
Что такое перпендикуляр?
Линии не всегда могут быть параллельными. На самом деле линии могут пересекаться, и когда они это делают, в их точке пересечения образуются углы. Когда две линии пересекаются под прямым углом, означая с точностью до 90 °, линии, которые образуют эти углы, называются перпендикулярными. В геометрии перпендикулярно означает под прямым углом. Когда линия встречается с другой линией под прямым углом или 90 °, образуется перпендикулярность, означающая, что обе линии перпендикулярны друг другу. Проще говоря, линия, которая делает правильный угол с другой, называется перпендикулярной линией. Например, стены перпендикулярны к полу или когда мы стоим вертикально, мы стоим перпендикулярно плоскости. Две перпендикулярные линии образуют четыре угла в их точках пересечения, все из которых равны и находятся под прямым углом.
Разница между параллельными и перпендикулярными
Определение параллельных и перпендикулярных
Две не вертикальные линии называются параллельными, если они равноудалены до конца бесконечных длин и имеют одинаковый наклон. В геометрии линии, которые одинаково удалены друг от друга во всех своих частях и никогда не пересекаются, называются параллельными линиями. Линии не всегда могут быть параллельными. Когда две пересекающиеся линии образуют четыре угла в их точках пересечения, все из которых равны и под прямым углом, то прямые называются перпендикулярными друг другу. Две прямые перпендикулярны, когда они пересекаются под прямым углом.
Две линии называются параллельными, когда они равноудалены друг от друга и никогда не пересекаются или не касаются друг друга. Поскольку линии одинаково удалены друг от друга, они имеют один и тот же наклон, означающий, что расстояние между линиями одинаково в разных частях. Проще говоря, наклон двух параллельных линий равен. Склоны перпендикулярных линий, с другой стороны, являются отрицательными обратными друг от друга, что означает, что линии пересекаются друг с другом под прямым углом.
Представление параллельных и перпендикулярных
Здесь две линии являются параллельными линиями и обозначаются как «∥».
Здесь линии перпендикулярны друг другу и обозначаются как «⊥».
Примеры параллельных и перпендикулярных
Параллельная и перпендикулярная: сравнительная таблица
Резюме параллельных Vs. Перпендикуляр
В двух словах, слово parallel относится к двум эквидистантным линиям, которые никогда не пересекаются или не касаются друг друга в любой точке. Поскольку линии одинаково отдалены, они имеют один и тот же наклон, а угол между ними равен нулю. С другой стороны, когда две прямые пересекаются под прямым углом, их называют перпендикулярными.Две пересекающиеся линии образуют четыре угла в их точках пересечения, все из которых равны значению углов 90 градусов. Склоны двух перпендикулярных линий противоположны друг другу.
Параллельность прямых
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.