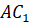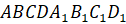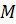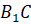Что такое параллельное проектирование
СОДЕРЖАНИЕ
Вступление
Вторая концепция заключается в том, что все действия по проектированию должны выполняться одновременно, т. Е. Одновременно. Идея состоит в том, что одновременный характер этих действий значительно увеличивает производительность и качество продукции. Таким образом, ошибки и изменения могут быть обнаружены на ранних этапах процесса проектирования, когда проект еще остается гибким. Обнаруживая и исправляя эти проблемы на раннем этапе, группа разработчиков может избежать ошибок, которые часто становятся дорогостоящими, поскольку проект переходит к более сложным вычислительным моделям и, в конечном итоге, к фактическому производству оборудования.
Параллельное проектирование заменяет более традиционный последовательный процесс проектирования, или «модель водопада». В Concurrent Engineering вместо этого используется итеративный или интегрированный метод разработки. Метод водопада движется линейно, начиная с требований пользователей и последовательно продвигаясь к проектированию и внедрению, пока у вас не будет готового продукта. В этой системе проектирования команда дизайнеров не будет быстро оглядываться назад или вперед с того шага, на котором она находится, чтобы исправить или предвидеть проблемы. В случае, если что-то пойдет не так, дизайн обычно нужно пересмотреть или сильно изменить. Параллельный или итеративный процесс проектирования способствует быстрому изменению стратегии, так что учитываются все аспекты жизненного цикла продукта, что позволяет использовать более эволюционный подход к проектированию. Разницу между двумя процессами проектирования можно увидеть графически на рисунке 1.
Существенная часть метода параллельного проектирования заключается в том, что отдельному инженеру предоставляется гораздо больше права голоса в общем процессе проектирования из-за совместной природы параллельного проектирования. Утверждается, что наделение дизайнера правом собственности способствует повышению производительности труда сотрудников и качества продукта, исходя из предположения, что люди, которым дано чувство удовлетворения и ответственности за свою работу, как правило, работают усерднее и создают более надежный продукт, а не сотруднику, которому поручена задача, которая мало влияет на общий процесс.
Проблемы, связанные с параллельным проектированием
Существуют поставщики услуг, которые специализируются в этой области, не только обучая людей эффективному параллельному проектированию, но и предоставляя инструменты для улучшения взаимодействия между членами команды.
Элементы
Кросс-функциональные команды
Кросс-функциональные группы включают людей из разных областей рабочего места, которые все вовлечены в конкретный процесс, включая производство, проектирование оборудования и программного обеспечения, маркетинг и т. Д.
Параллельная реализация продукта
Одновременное выполнение нескольких задач, например одновременное проектирование различных подсистем, имеет решающее значение для сокращения времени проектирования и лежит в основе параллельного проектирования.
Дополнительный обмен информацией
Дополнительный обмен информацией помогает свести к минимуму вероятность того, что параллельная реализация продукта приведет к неожиданностям. «Инкрементальный» означает, что как только новая информация становится доступной, она передается и интегрируется в дизайн. Межфункциональные группы важны для эффективного и своевременного обмена информацией.
Комплексное управление проектами
Интегрированное управление проектом гарантирует, что кто-то несет ответственность за весь проект, и эта ответственность не передается после выполнения одного из аспектов работы.
Определение
Используются несколько определений параллельной разработки.
Использование CE
В настоящее время CE используют несколько компаний, агентств и университетов. Среди них можно отметить:
Параллельное проектирование
Концепция параллельного проектирования подразумевает одновременную совместную работу над изделием максимально возможного количества инженеров, а также привлечение к работе смежников, на максимально ранних этапах работ.
«Все этапы работы над двигателем проходят не последовательно, а как правило, параллельно. В результате общий цикл разработки двигателя сокращается».
Юрий Зеленков, директор по ИТ НПО «Сатурн»*
Существующие подходы к инженерной подготовке производства характеризуются последовательными процессами, когда следующая стадия начинается только после завершения предыдущей, что существенно увеличивает вероятность ошибок и переделок и приводит к увеличению и сроков, и стоимости изделия. Альтернативой является идея параллельного проектирования.
Основные положения концепции
Одновременная работа над изделием максимально возможного количества инженеров.
Привлечение к совместной работе над изделием смежников, на максимально ранних этапах работы.
Основные преимущества концепции
Идеи параллельного проектирования, при их воплощении в жизнь позволяют значительно сократить срок разработки продукции (до 70%) и внесения изменений (65-90%). Что в свою очередь ведет к резкому ускорению выхода на рынок востребованной продукции, снижения затрат и одновременного повышения качества.
Способ реализации концепции
Достижению подобных результатов способствуют два основных приема: интеграция и параллелизм.
Интеграция означает, что специалисты функциональных подразделений, вовлеченных в процессы инженерной подготовки производства, и другие заинтересованные лица должны работать в тесной взаимосвязи. Такая интеграция усилий реально отражается на улучшении качества конечной продукции.
Параллелизм автоматически сокращает сроки разработки продукции и внесения изменений, так как решение задач выполняется параллельно, а не последовательно. При использовании этого подхода к инженерной подготовке производства, многие проблемы, которые могут возникнуть на более поздних стадиях жизненного цикла, выявляются и решаются на ранних стадиях.
Предполагается, что команда должна параллельно решать разнообразные специальные конструкторские задачи, обеспечивающие достижение целей разработки. Каждая подобная задача связана с реализацией определенных жизненно важных конструкторских требований, в свою очередь влияющих на ряд других требований. Именно эти взаимосвязи зачастую упускают из вида при традиционном, последовательном подходе к разработкам новой продукции.
Примеры эффективного использования
Предлагаемая концепция гарантирует выполнение всей совокупности требований к продукции, что обеспечивает удовлетворение запросов потребителей, соблюдение требований законодательства, оптимальную производственную технологичность продукции.
Концепция параллельного проектирования реализуется за счет соответствующего функционала PDM/CAD/CAM/CAE-систем (Teamcenter, NX, NX CAM) и организационных мероприятий.
Основы параллельного проектирования
Определение понятия и рассмотрение существующих в математике теорий параллельного проектирования. Характеристика и доказательство основных свойств параллельного проектирования. Установление связи между параллельным проектированием и решением задач.
| Рубрика | Математика |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 03.04.2016 |
| Размер файла | 987,0 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Министерство образования Иркутской области
Государственное бюджетное профессиональное образовательное учреждение Иркутской области
«Ангарский политехнический техникум»
на тему: «Параллельное проектирование»
по дисциплине: Математика
Выполнила: Бобова Юлия
1. Что такое параллельное проектирование
2. Свойства параллельного проектирования
3. Решение задач с помощью параллельного проектирования
Список использованной литературы
Геометрия, наравне со многими другими разделами математики, дает возможность почувствовать красоту математики вообще и может стать для кого-то началом пути в «большую науку». Кроме того, каждый любитель геометрии имеет шанс открыть нечто новое и пополнить ее сокровищницу собственной драгоценной находкой, ибо геометрия поистине неисчерпаема!
А. Г. Мякишев «Элементы геометрии треугольника»
Геометрия многолика. И одну задачу можно решить большим количеством разных способов. В школе изучается лишь малая часть того, что принято называть геометрией. Моя работа называется «Помогает параллельное проектирование». Работа показывает, что параллельное проектирование позволяет не только строить проекции фигур и пространственных тел, но еще и облегчает решение ряда задач, связанных с нахождением отношений отрезков и нахождения отношения площадей.
В этой работе рассмотрен удивительный способ для решения ряда задач. Способ, не описанный в школьном учебнике. Способ, основанный на свойствах параллельного проектирования таких как: любой треугольник при помощи параллельного проектирования можно перевести в правильный; при параллельном проектировании сохраняются отношения отрезков и площадей фигур.
К сожалению, параллельное проектирование очень редко используется. Оно не упоминается в школьной программе до десятого класса, хотя оно могло бы существенно упростить решение некоторых задач по геометрии. К тому же я считаю эту тему очень интересной и стоящей, ведь мы встречаемся с параллельным проектированием каждый день.
Цель: исследование параллельного проектирования и его свойств, а также применение параллельного проектирования при решении задач.
1. Изучение теории по параллельному проектированию
2. Доказательство некоторых свойств параллельного проектирования
3. Установление связи между параллельным проектированием и решением задач
4. Выполнение практической части.
1. Что такое параллельное проектирование
Ветреный летний день.
Прижавшиеся к стене
И тень интересней мне.
Иосиф Бродский. «Сидя в тени»
математика параллельный проектирование
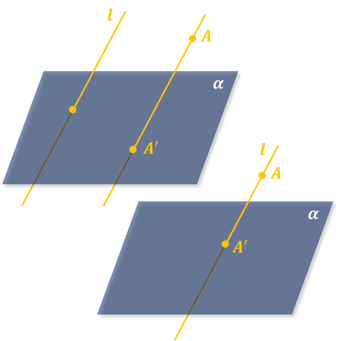
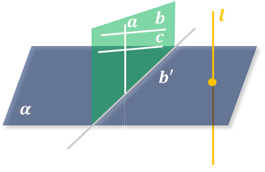
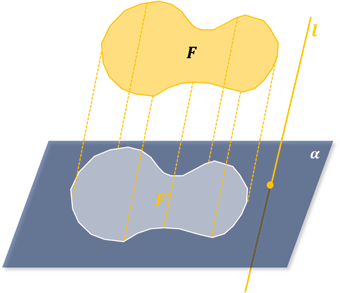
Таким образом, каждой точке A пространства сопоставляется ее проекция A’ на плоскость р. Это соответствие называется параллельным проектированием на плоскость р в направлении прямой l.
Мы не раз встречались с параллельным проектированием в жизни. Например, наша тень в солнечный день на ровном асфальте есть наша параллельная проекция ( солнечные лучи приближенно можно считать параллельными ввиду большой удалённости Солнца от Земли).
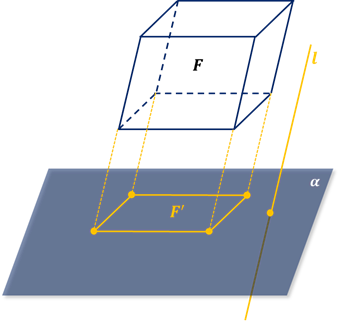
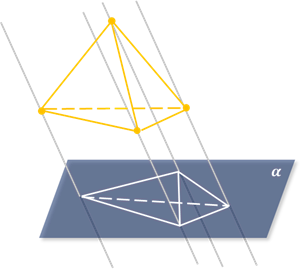
Параллельное проектирование позволяет получать наглядные изображения пространственных (трёхмерных) фигур на (двумерной) плоскости (рис. 4). Дело в том, что параллельное проектирование сохраняет ряд важных черт изображаемой фигуры. Перечислим основные свойства параллельного проектирования в предложении, что направление проектирования не параллельно рассматриваемым прямым и отрезкам (в противном случае их проекциями являются точки.
2. Свойства параллельного проектирования
Свойство 2. Две параллельные прямые проектируются либо в две параллельные прямые, либо в одну и ту же прямую. Проекции параллельных отрезков лежат либо на параллельных прямых, либо на одной прямой.
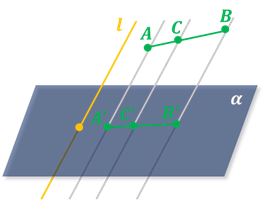
Свойство 3. Длины проекций параллельных отрезков или отрезков лежащих на одной прямой, пропорциональны длинам этих отрезков
Свойство 4. При параллельном проектировании сохраняется отношения площадей двух любых фигур, если направление проектирования не параллельно плоскостям фигур.
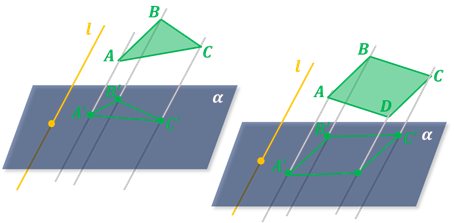
Свойство 5. Любой треугольник можно рассматривать как параллельную проекцию данного треугольника с точностью до подобия.
Доказательство свойства 5: Докажем, что в общем случае треугольник любой формы может служить параллельной проекцией равностороннего треугольника.
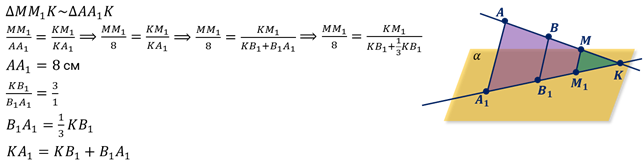
Действительно, пусть дан произвольный треугольник ABC в плоскости р Построим на одной из его сторон. например, AC равносторонний треугольник AB1C так, чтобы точка B1 не принадлежала плоскости р. Обозначим через l прямую, проходящую через точки B1 и B. Тогда ясно, что треугольник ABC является параллельной проекцией треугольника AB1C на плоскость р в направлении прямой l.
3. Решение задач с использованием параллельного проектирования
Задача №1. Доказать, что прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжений ее боковых сторон, делит основания трапеции пополам.
Решение: Изобразим на плоскости в (рис. 11) и мысленно параллельно спроектируем его на плоскость б так, чтобы треугольник AMD перешел в A1M1D1 равнобедренный треугольник (рис.12).
Из свойств параллельного проектирования следует, что проекцией трапеции ABCD является трапеция A1B1C1D1, то есть B1C1 // A1D1. Далее, так как треугольник A1M1D1 равнобедренный, то его высота M1H1 совпадает с медианой и является осью симметрии треугольника.
Следовательно, точка C1 переходит в точку B1, прямая A1C1 переходит в прямую B1D1, а поэтому N1 точка пересечения прямых A1C1 и B1D1 находится на оси симметрии, то есть на прямой M1H1.
Что и требовалось доказать.
1. Анализ теоретического материала по параллельному проектированию позволил узнать свойства и область применения параллельного проектирования.
2. Решение практических задач показало, что многие задачи, даже очень сложные можно решить с помощью параллельного проектирования, сэкономив при этом и время, и силы.
3. Я узнала много нового и интересного, работая над данной темой. Многие задачи оказываются не такими трудными, как казалось бы. Это действительно занимательно и увлекательно. Так же эта прекрасная тема пригодится мне в будущем, при изучении стереометрии в старших классах.
1) А. Ю. Калинин, Д. А. Терешин. «Стереометрия 10». МФТИ 1996.
2) А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. «Неожиданный шаг или сто тринадцать красивых задач». Киев, Агрофирма «Александрия» 1993.
Размещено на Allbest.ru
Подобные документы
Методика нахождения различных решений геометрических задач на построение. Выбор и применение методов геометрических преобразований: параллельного переноса, симметрии, поворота (вращения), подобия, инверсии в зависимости от формы и свойств базовой фигуры.
курсовая работа [6,4 M], добавлен 13.08.2011
Основные понятия и предложения. Дополняемость в гильбертовых пространствах. Задача о дополняемости. Доказательство замкнутости ядра. Формула изменения коэффициентов Фурье при сдвиге на некоторое вещественное число.
дипломная работа [105,7 K], добавлен 08.08.2007
Ознакомление с принципами параллельного переноса, растяжения и сжатия функции y=f(x) вдоль осей Ох и Оу. Рассмотрение правил симметрического отображения функции относительно осей координат. Особенности сложения и умножения ординат точек графиков.
презентация [356,6 K], добавлен 16.12.2011
Сущность и графическое отображение игры на преследование, ее математический смысл и формулирование соответствующих теорем. Стратегия параллельного сближения и ее обоснование. Порядок преследования на плоскости с одним или несколькими преследователями.
творческая работа [24,9 K], добавлен 03.01.2010
Сущность и структура орнамента, его предназначение и классификация (по характеру композиции и поверхности, содержанию элементов, количеству цветов). Особенности построения орнамента с помощью симметрии относительно прямой и параллельного переноса.
презентация [4,5 M], добавлен 19.11.2012
Параллельное проектирование. Изображение пространственных фигур
Урок 33. Подготовка к ЕГЭ по математике
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Параллельное проектирование. Изображение пространственных фигур»
В стереометрии большое значение имеет умение наглядно изображать неплоские фигуры на плоскости. Вы знаете, что когда в планиметрии на листе бумаги изображают плоскую фигуру, то все точки изображённой фигуры лежат на плоскости листа. В стереометрии же рассматриваются фигуры, у которых не все точки расположены в одной плоскости. Поэтому надо знать правила, по которым изображают на плоскости пространственные фигуры.
Итак, зачастую для изображения на плоскости (например, на листе бумаги) геометрических фигур, расположенных в пространстве, используется параллельное проектирование. Определяется оно следующим образом.
Пусть 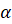
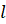
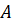
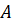
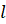
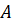
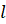
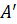
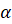
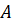
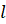
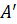
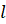
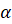
Точка 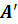
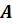
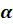
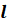
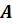
Плоскость 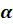
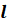
Все прямые, параллельные прямой 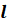
Пусть 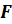
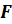
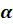
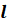
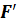
Заметим, что проекция заданной фигуры зависит от выбора плоскости проекций и проектирующей прямой.
Вспомним основные свойства параллельного проектирования при условии, что проектируемые отрезки и прямые не параллельны прямой, задающей направление проектирования.
1. Проекция прямой есть прямая, а проекция отрезка — отрезок.
2. Проекции параллельных прямых параллельны или совпадают.
3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.
Следствие. При параллельном проектировании середина отрезка проектируется в середину его проекции.
При параллельном проектировании могут искажаться размеры отрезков и углы, но обязательно сохраняется параллельность прямых.
Если точка делит отрезок в отношении 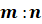
Центр правильного треугольника отображается в точку пересечения медиан проекции этого треугольника, центр квадрата — в точку пересечения диагоналей проекции квадрата.
А теперь давайте поговорим об изображении пространственных фигур.
Рассмотренные свойства параллельного проектирования применяются при выполнении рисунков (изображений фигур), иллюстрирующих теоремы и задачи стереометрии.
Изображением фигуры 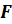
Выполняя изображения фигур, расположенных в пространстве, необходимо учитывать свойства, сохраняющиеся при параллельном проектировании, а в остальном изображение может быть произвольным. Важно только, чтобы изображения рассматриваемых фигур были наглядными и давали верное представление о них.
При различном выборе плоскости проекций и направления проектирования получаются различные проекции данной фигуры, а значит, и различные её изображения.
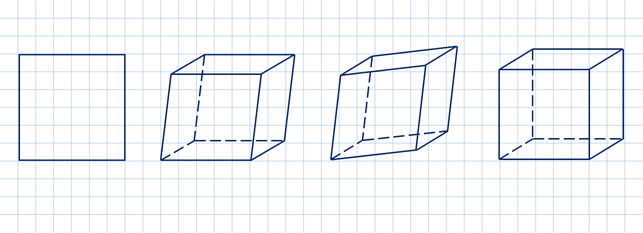
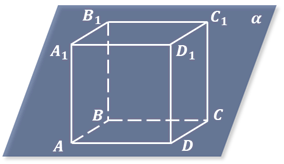
Например, вы видите фигуры, которые являются изображениями куба.
Причём изображение куба, данное на первом рисунке, не даёт представления о кубе, наглядным является изображение, которое дано на последнем рисунке.
При построении изображений плоских фигур, расположенных в пространстве, предполагается, что плоскости рассматриваемых фигур не параллельны направлению проектирования.
Итак, проекцией треугольника может быть любой треугольник.
При этом величины углов и отношение длин непараллельных сторон не сохраняются, но при этом медианы треугольника отображаются в медианы его проекции. В частности, за изображение прямоугольного, равнобедренного, равностороннего треугольников можно принять любой треугольник.
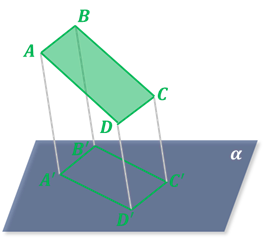
Параллелограмм проектируется в параллелограмм, так как параллельные прямые сохраняют параллельность.
В частном случае за изображение прямоугольника, квадрата, ромба можно принять любой параллелограмм.
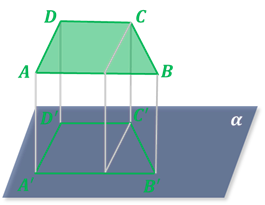
Трапеция проектируется в другую трапецию, но с сохранением параллельности оснований.
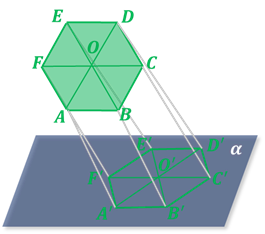
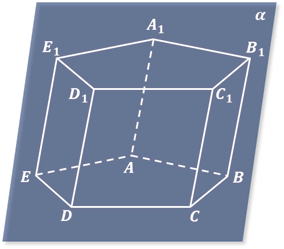
Правильный шестиугольник проектируется в искажённый шестиугольник с сохранением параллельности противолежащих сторон.
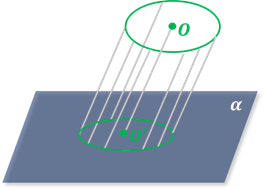
Окружность проектируется в эллипс, большая ось которого имеет длину, равную диаметру окружности.
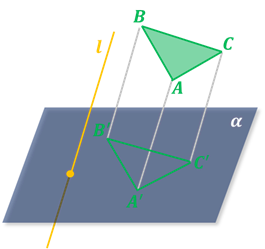
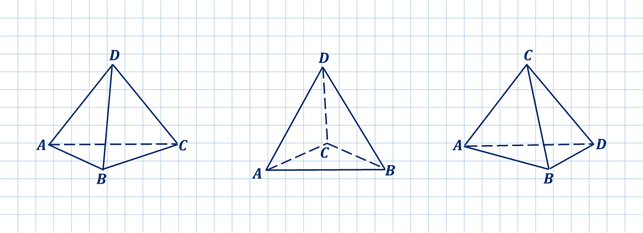
При изображении пространственных фигур пользуются тем фактом, что фигуру, состоящую из сторон и диагоналей любого выпуклого или невыпуклого четырёхугольника, можно считать изображением треугольной пирамиды при определённом выборе направления проектирования и плоскости, на которую проектируется эта пирамида.
Например, фигуры, изображённые на экране, являются изображениями треугольной пирамиды при соответствующем выборе направления проектирования.
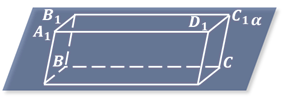
Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами.
При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами.
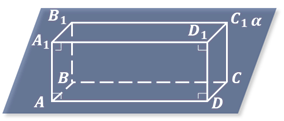
Аналогичным образом изображается прямоугольный параллелепипед.
Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий её основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы.
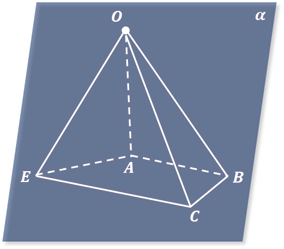
Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий её основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить её с вершинами многоугольника. Полученные отрезки будут изображать боковые рёбра пирамиды.
Для изображения цилиндра достаточно изобразить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований.
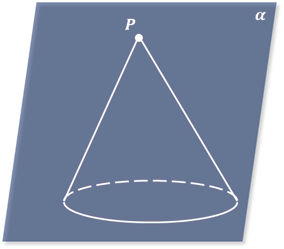
Для изображения конуса достаточно изобразить его основание в виде эллипса, отметить вершину и провести через неё две образующие, являющиеся касательными к этому эллипсу.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. Точки 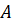
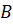
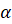
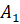
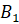
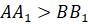
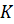
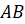
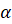
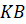
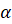
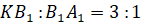
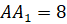
Задача вторая. На диагонали