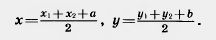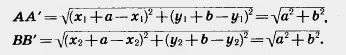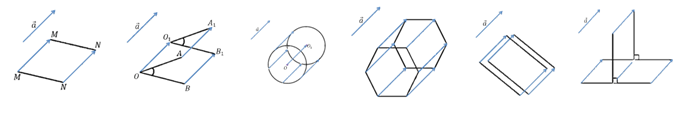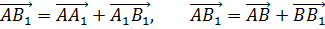Что такое параллельный перенос

Параллельный перенос

Паралле́льный перено́с или трансляция [1] ― частный случай движения, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние. Иначе, если ― первоначальное, а ― смещенное положение точки, то вектор ― один и тот же для всех пар точек, соответствующих друг другу в данном преобразовании.

Содержание

Определение

Параллельный перенос все точки пространства перемещает в одном и том же направлении на одно и то же расстояние. Иначе, если ― первоначальное, а ― смещенное положение точки, то вектор ― один и тот же для всех пар точек, соответствующих друг другу в данном преобразовании.

Координатное представление

На плоскости параллельный перенос выражается аналитически в прямоугольной системе координат при помощи

где вектор .

Свойства

Параллельный перенос в разных областях науки

Примечания

Полезное

Смотреть что такое «Параллельный перенос» в других словарях:

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС — преобразование плоскости или пространства, при котором все точки смещаются в одном и том же направлении на одно и то же расстояние … Большой Энциклопедический словарь

параллельный перенос — параллельная передача — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы параллельная передача EN parallel transfer … Справочник технического переводчика

параллельный перенос — преобразование плоскости или пространства, при котором все точки смещаются в одном и том же направлении на одно и то же расстояние. * * * ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС, преобразование плоскости или пространства, при котором все точки… … Энциклопедический словарь

параллельный перенос — transliacija statusas T sritis fizika atitikmenys: angl. translation vok. Translation, f rus. параллельный перенос, m; трансляция, f pranc. translation, f … Fizikos terminų žodynas

Параллельный перенос — преобразование пространства или его части (например, переход от одной фигуры к другой), при котором все точки смещаются в одном и том же направлении на одно и то же расстояние. Совокупность всех П. п. как на плоскости, так и в… … Большая советская энциклопедия

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС — частный случай движения, при к ром все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние. Иначе, если М первоначальное, а М смещенное положение точки, то вектор один и тот же для всех пар точек,… … Математическая энциклопедия

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС — преобразование плоскости или пространства, при к ром все точки смещаются в одном и том же направлении на одно и то же расстояние … Естествознание. Энциклопедический словарь

Перенос — Перенос: В Викисловаре есть статья «перенос» Перенос (типографика) разрыв слова так, что начало его оказывается на одной строчке, а конец на другой. Также знак, устанавливаемый в месте разрыва. Перенос (арифметика) приёмы, применяемые … Википедия

одновременный перенос — параллельный перенос — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы параллельный перенос EN simultaneous carry … Справочник технического переводчика

Символы Кристоффеля — являются координатными выражениями аффинной связности, в частности связности Леви Чивиты. Названы в честь Элвина Бруно Кристоффеля (1829 1900), Символы Кристоффеля используются в дифференциальной геометрии, общей теории относительности и близких… … Википедия

Источник

Что такое параллельный перенос

Параллельный перенос и его свойства

Содержание

Общие сведения о параллельном переносе

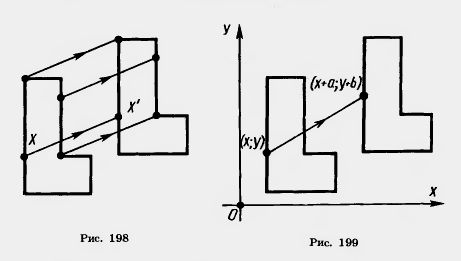
Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (рис. 198). Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении», которое само нуждается в точном определении. В связи с этим параллельному переносу мы дадим другое, отвечающее тому же наглядному представлению, но уже строгое определение.

Введем на плоскости декартовы координаты х, у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами x’ = x + а, у’ = у + b.

Эти формулы выражают координаты х’, у’ точки, в которую переходит точка (х; у) при параллельном переносе.

Свойства параллельного переноса

Параллельный перенос есть движение.

Действительно, две произвольные точки А(х₁; у₁) к В (х₂; у₂) переходят при параллельном переносе в точки А’ (х₁ +а; у₁ + b), В'(х₂ + а; y₂+b). Поэтому
АВ 2 =(х₂-х₁) 2 + (у₂-у₁ ) 2

Отсюда АВ=А’В’. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать.

Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

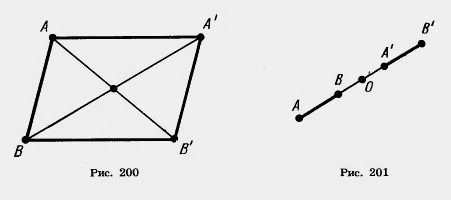
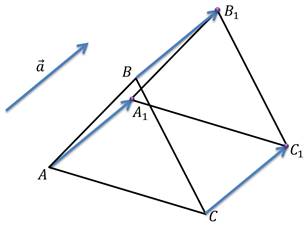
Действительно, пусть точки A (x₁; y₁) и В (x₂; y₂) переходят в точки A'(x₁+а; y₁ + b) и В’ (х₂ + а; y₂ + b) (рис. 200). Середина отрезка АВ’ имеет координаты

Те же координаты имеет и середина отрезка А’В. Отсюда следует, что диагонали четырехугольника АА’В’В пересекаются и точкой пересечения делятся пополам. Значит, этот четырехугольник — параллелограмм. А у параллелограмма противолежащие стороны А А’ и ВВ’ параллельны и равны.

Заметим, что у параллелограмма АА’В’В параллельны и две другие противолежащие стороны — АВ и А ‘В’. Отсюда следует, что при параллельном, переносе прямая переходит в параллельную прямую (или в себя).

Замечание. В предыдущем доказательстве предполагалось, что точка В не лежит на прямой АА’. В случае, когда точка В лежит на прямой АА’, точка В’ тоже лежит на этой прямой, так как середина отрезка АВ’ совпадает с серединой отрезка ВА’ (рис. 201). Значит, все точки А, В, А’, В’ лежат на одной прямой. Далее,

Таким образом, в этом случае точки АиВ смещаются по прямой АВ на одно и то же расстояние 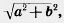а прямая АВ переходит в себя.

Повторение темы о параллельном переносе

Мы с вами уже познакомились с такой темой, как параллельный перенос. На этом уроке вы узнали, что такое преобразование на плоскости, где все точки перемещаются на одно и то же расстояние, считается параллельным переносом.

Из данного урока, каждому из вас стало понятно, что параллельный перенос является движением, так как при таком переносе любая прямая переходит в такую же параллельную ей прямую.

Если мы посмотрим на рисунок, то можем наглядно представить такое движение, как сдвиг площади в направлении данного вектора на его длину.

Свойства, которыми обладает параллельный перенос в пространстве

• Во-первых, параллельный перенос является движением;
• Во-вторых, при выполнении этого действия все точки смещаются по параллельным прямым и притом на одно и то же расстояние;
• В-третьих, при таком переносе прямая имеет свойство переходить в такую же параллельную прямую или в себя саму;
• В-четвертых, независимо от того, какими точками были A и A’, но точка A переходит в точку A’.
• В-пятых, при таком переносе, т.е параллельном переносе в пространстве, в любом случае плоскость имеет свойство переходить в себя саму или же такую же параллельную ей плоскость.

Истрия и применение в науке

Как правило, в каждого понятия есть свой первооткрыватель, но автор параллельного переноса в пространстве, на жаль, нам неизвестен. А вот применение параллельного переноса в пространстве довольно широко. Как правило, такой перенос используют при преобразовании графической функции в математике, в механике, а также в кристаллографии.

Но если рассматривать трансляция или кристаллографию, то в этом случае перенос приобретает симметричное преобразование, в котором узел пространственной решётки должен совпасть с идентичным ближайшим узлом. В принципе, трансляцию можно отнести к частному случаю параллельного переноса, так как при сдвиге на определенный вектор ее свойства в данной системе не изменяются, а являются вектором трансляции и для нее свойственна трансляционная симметрия.

Примеры из жизни

В повседневной жизни мы с вами также постоянно сталкиваемся с примерами параллельного переноса в пространстве. Таким наглядным примером может быть, применяемая в строительной индустрии скользящая опалубка, этот процесс мы можем наблюдать и при перестановке мебели в квартире, да и следы от подошвы нам также напоминают о параллельном переносе в пространстве.

А также, параллельный перенос можно встретить и в таких необычных ситуациях:

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

Источник

Параллельный перенос

Урок 11. Геометрия 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Параллельный перенос»

Сегодня на уроке мы вспомним, какое отображение плоскости на себя мы называли параллельным переносом, введём понятие параллельного переноса в пространстве. Проверим, будет ли параллельный перенос движением пространства.

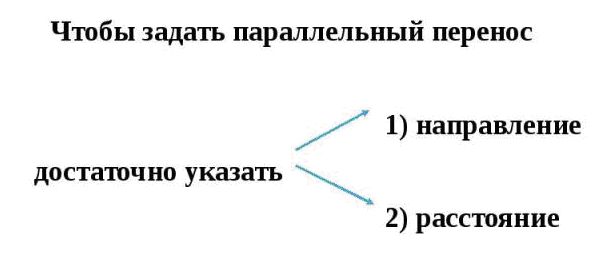
Вернёмся в планиметрию и вспомним, что параллельным переносом мы называли преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении и на одно и то же расстояние. Мы говорили, что для того, чтобы задать перенос достаточно задать вектор.

Другими словами, параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка отображается в такую точку , что вектор равен вектору .

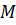
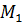
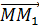
То, что параллельный перенос является примером движения плоскости, мы уже доказывали. Давайте вспомним это доказательство.

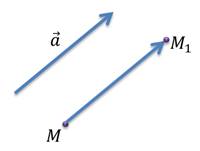
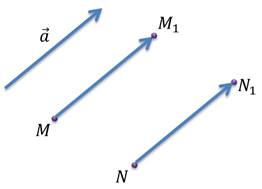
Пусть при параллельном переносе на вектор точки и отображаются в точки и . Так как векторы и , то значит, эти векторы равны между собой . То есть они параллельны и их длины равны, поэтому четырёхугольник – параллелограмм. Следовательно, , то есть расстояние между точками и равно расстоянию между точками и .

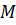
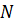
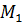
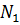
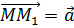
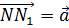
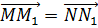
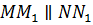
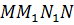
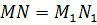
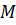
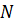
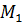
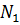
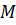
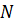
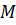
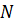
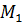
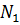
Случай, когда точки и лежат на прямой параллельной вектору , вы можете рассмотреть самостоятельно. Но и в этом случае расстояние между точками и будет равно расстоянию между точками и .

Таким образом, параллельный перенос сохраняет расстояние между точками и поэтому представляет собой движение. Это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

В планиметрии мы говорили, что параллельный перенос обладает некоторыми свойствами.

Свойства параллельного переноса:

· При параллельном переносе отрезок переходит в равный ему отрезок.

· Угол переходит в равный ему угол.

· Окружность переходит в равную ей окружность.

· Любой многоугольник переходит в равный ему многоугольник.

· Параллельные прямые переходят в параллельные прямые.

· Перпендикулярные прямые переходят в перпендикулярные прямые.

Теперь давайте определим, что мы будем понимать под параллельным переносом в пространстве.

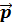
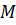
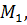
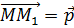
Параллельным переносом на вектор называется такое отображение пространства на себя, при котором любая точка переходит в такую точку что .

Проверим, будет ли параллельный перенос в пространстве примером движения пространства.

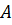
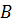
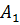
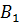
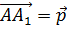
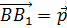
При параллельном переносе точки пространства и переходят в такие точки и , что вектора и .

Сложим по правилу треугольника векторы

Поскольку левые части равенств равны, значит, равны и правые части равенств.

Значит, можно записать, что .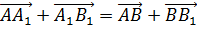

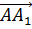
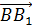
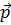
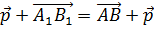
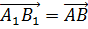
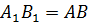
Заменим вектора и на вектор . Получим, что . Отсюда получаем, что вектор . Поскольку векторы равны, значит, равны и их длины, то есть . То есть расстояние между точками при параллельном переносе в пространстве сохраняется, значит, параллельный перенос в пространстве также является движением, но уже не плоскости, а пространства.

Сформулируем свойства параллельного переноса.

Свойства параллельного переноса:

· Параллельный перенос является примером движения пространства.

· При параллельном переносе точки смещаются по параллельным или совпадающим прямым на одно и то же расстояние.

· При параллельном переносе прямая переходит в параллельную прямую (или сама в себя).

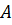
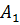
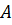
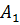
· Каковы бы не были две точки и , существует, и притом единственный, параллельный перенос, при котором точка переходит в точку .

· При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.

Движение в пространстве обладает теми же свойствами, что и движение плоскости.

Свойства движения пространства:

· Движение сохраняет расстояние между точками.

· При любом движении пространства отрезок отображается на отрезок, прямая – в прямую, плоскость – в плоскость.

Решим несколько задач.

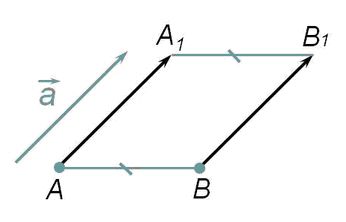
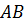
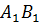
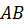
Задача: начертить отрезок и вектор . Построить отрезок , который получится из отрезка параллельным переносом на вектор .

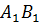
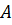
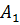
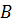
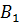
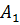
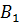
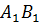
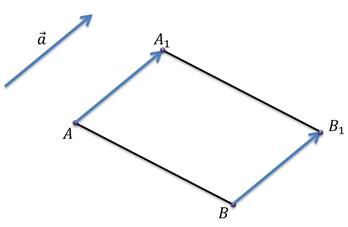
Решение: для того, чтобы построить отрезок , отобразим точку в точку , точку в точку с помощью параллельного переноса. Тогда соединив точки , мы получим отрезок .

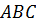
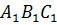
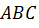
Задача: начертить треугольник и вектор . Построить треугольник , который получится из треугольникa параллельным переносом на вектор .

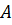
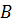
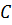
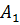
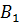
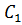
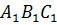
Решение: отобразим с помощью параллельного переноса точки , , в точки , ,. Соединив полученные точки, мы получим искомый треугольник .

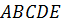
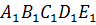
Задача: начертить пятиугольник и вектор . Построить пятиугольник , который получится из пятиугольника параллельным переносом на вектор .

Решение: решать эту задачу будем аналогично тому, как мы решали предыдущую задачу. Отобразим каждую вершину пятиугольника с помощью параллельного переноса на вектор . Соединим получившиеся точки и получим искомый пятиугольник .

Сегодня на уроке мы вспомнили, что мы понимали под параллельным переносом в планиметрии. Ввели понятие параллельного переноса в пространстве. Сформулировали основные свойства параллельного переноса, движения пространства.

Источник