Что такое параметры формы и параметры положения
Определение параметров формы и положения кривых 2-го порядка
Дата публикации: 22.02.2017 2017-02-22
Статья просмотрена: 876 раз
Библиографическое описание:
Мурадов, Ш. К. Определение параметров формы и положения кривых 2-го порядка / Ш. К. Мурадов, М. К. Халимов, З. Э. Мирзалиев, Г. С. Рамазанова. — Текст : непосредственный // Молодой ученый. — 2017. — № 7 (141). — С. 454-457. — URL: https://moluch.ru/archive/141/39580/ (дата обращения: 23.12.2021).
В настоящей статье рассматриваются определения формы и положения кривых 2-го порядка на плоскости и в пространстве, которые применяются для задания этих кривых и для определения положения плоскостей пересекающих поверхностей 2-го порядка по заданному коническому сечению.
Ключевые слова: прикладная геометрия, инженерная графика, графические дисциплины, кривые 2-го порядка, эллипс, гипербола, парабола, окружность, параметры, положения, формы, параметрическая мощность, центр
Многие годы в Ташкентском государственном педагогическом университете Республики Узбекистан подготавливаются магистры по специальности — 5А110802 — Инженерная графика и теория дизайна. В связи с этим в ТГПУ имени Низами как головной педагогический университет систематически совершенствуются типовые учебные и тематические планы по дисциплине «Прикладная геометрия» с новыми требованиями. При этом особенно уделяются внимание методам исследования кривых линии и поверхностей, которые часто встречаются на различных отраслях производства, как в машиностроении, так и в сооружениях строительства. Как известно, пространство заполнено множеством геометрических фигур для выделения из них определенных фигур требуется некоторые дополнительные условия. Например, определение параметров положения и формы геометрических фигур отвечающим наперед заданным условиям. Образование и построение кривых линии 2-го порядка часто встречаются в учебном процессе для построения линии пересечения кривых поверхностей 2-го порядка с плоскостью и между собой. Поэтому вопрос определения параметров положения и формы кривых линии 2-го порядка имеют особое место для преподавания графических дисциплин.
Параметры, определяющие положения кривых 2-го порядка называем параметрами положения кривых 2-го порядка. Параметры, определяющие вид (форму) кривых 2-го порядка, называются параметрами формы этих кривых.
В настоящей статье рассматривается один из способов определения параметров положения и формы кривых линии 2-го порядка, как на плоскости, так и в пространстве.
2.1. Параметры положение произвольной параболы на плоскости можно определить заданием её вершины (или фокуса) и направлением оси параболы (рис. 3). Задание вершины параболы (точка) на плоскости определяется двумя параметрами, заданием направления оси параболы определяет еще один параметр. Следовательно, число параметров положения произвольной параболы на плоскости равно трем. Совокупность парабол на плоскости четырех параметрическое множество, мощность которого равна ∞ 4 (один — параметр формы. Три — параметры положения).
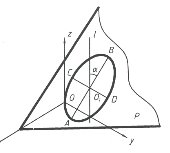
Известно, что из кривых второго порядка эллипс и гиперболы относятся к группе центральных кривых. Они имеют центр (точка) и главные оси, которые определят формы этих кривых. Поэтому определение параметров формы и положения эллипса и гиперболы будим рассматривать аналогично.
Выше приведенные соображения можно использовать для задания кривых 2-го порядка и для определения положения плоскостей пересекающих поверхности 2-го порядка по заданному коническому сечению.
Необходимо отметить, что изучая способы образования и задания некоторых других кривых более высокого порядка, можно определить число параметров формы и положение этих кривых.
Выше приведенные сведения для определения количество параметров формы и положения кривых 2-го порядка как на плоскости и в пространстве можно определить по таблице № 1.
Параметризация геометрических моделей (Parameterization of geometric models)
Теория параметризации позволяет формализовать процесс определения числа параметров, необходимых для задания геометрического объекта. Эта теория также позволяет решить обратную задачу – определить размерность множества решений поставленной задачи еще перед разработкой алгоритма ее решения. Кроме этого, с помощью теории параметризации можно исследовать возможности определения новых геометрических объектов.
Параметры – независимые числовые величины, которые позволяют выделить геометрический объект из N-параметрического множества объектов в заданной системе параметризации.
Система параметризации – совокупность заданных геометрических элементов (примитивов) и геометрических условий, которые ставят в соответствие каждому объекту набор параметров.
N-параметрическое множество – множество объектов, для выделения одного из которого необходимо связать N параметров.
Параметрическое число объекта – количество параметров (N), которое выделяет единственный объект из N-параметрического множества объектов.
Основы метода параметризации объектов
Из точек можно образовать линию, непрерывно перемещая точку в пространстве. Аналогично можно образовать поверхность, перемещая линию в пространстве. Для определения геометрических объектов (Г.О.) нет необходимости указывать положение всех принадлежащих ему точек. Достаточно лишь указать определитель – совокупность элементов (геометрическая часть), из которых можно образовать Г.О., и условия их перемещения (алгоритм).
Геометрическая часть определителя может быть выражена через другой определитель (геометрическая часть + алгоритм). В конечном итоге геометрическая часть выражается точками, а точки – параметрами, определяющими их взаимное положение.
Размерность пространства. Определение параметрического числа объекта
Параметры определяются суммированием параметров точек, через которые в конечном итоге выражается геометрическая часть определителя. При этом следует иметь в виду, что количество параметров зависит от размерности пространства. Различают:
Определителем отрезка являются 2 фиксированные точки. Следовательно, в пространстве R3 отрезок определяется 6-ю параметрами (N=3+3), в плоскости 4-я (N=2+2). Пирамида с треугольным основанием определяется 4-я фиксированными точками в пространстве и 12 параметрами (N=4*3).
Не все геометрические объекты было бы правильно определять через фиксированные точки. Так, например, если определить прямую по 2-м фиксированным точкам, то окажется, что мы имеем на плоскости 4-х параметрическое множество прямых (на самом деле 2-х параметрическое). Введём новое понятие текущей точки линии (поверхности).
Текущая точка линии – это точка, которая может перемещаться по линии. Т.е., в этом случае один параметр точки не зафиксирован. Поэтому текущая точка линии в пространстве R2 определяется лишь одним параметром, а в пространстве R3 лишь двумя параметрами.
Текущая точка поверхности – это точка, которая может перемещаться по поверхности. Т.е., в этом случае два параметра точки не зафиксированы. Поэтому текущая точка поверхности определяется лишь одним параметром.
Зная параметрические числа прямых и плоскостей, можно их использовать для параметризации более сложных объектов. Например, треугольник можно определить как фигуру, ограниченную прямыми, а пирамиду – как фигуру, ограниченную плоскостями.
Каждая линия на плоскости определяется 2-я параметрами, соответственно, треугольник определяется 6 параметрами.
Аналогично рассуждая, получим, число параметров для пирамиды с четырехугольным основанием будет 15 (по три для каждой из плоскостей). Однако, их не 15, а 14. Где прокол? В этом случае необходимо учитывать, что три боковые плоскости, пересекаясь, определяют одну точку (вершину пирамиды) и, следовательно, для определения 4-й боковой плоскости необходимо добавить еще только 2 текущих точки поверхности (2 параметра) вместо 3-х.
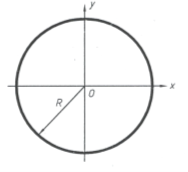
Определитель фигуры может быть различным, но корректная параметризация объекта при элементарных знаниях геометрии обеспечит один и тот же результат. Например, определителем окружности может быть одна фиксированная точка (центр окружности) и одна текущая точка, а также определителем окружности могут быть 3 текущие точки. В обоих случаях получаем один и тот же результат – 3 параметра.
На рисунках ниже видно, что геометрические условия заменяют параметры. Например, прямая, параллельная заданной определяется не 2-я, а 1-м параметром (расстоянием к заданной прямой). Одним параметром вместо 2-х определяется и прямая, касательная к заданной линии. Число параметров, необходимых для определения треугольника, уменьшается при наличии симметрии.
Следовательно, при расчете параметрического числа геометрического объекта необходимо не только просуммировать параметрические числа геометрических элементов определителя, но и вычесть параметрические числа геометрических условий.
N = N1+ N2+…+ Nk — (Ny1+ Ny2+…+ Nyp)
Но для этого необходимо уметь параметризовать геометрические условия.
Параметризация геометрических условий
Размерность геометрического условия Ny определяется разницей параметрического числа объекта, несвязанного условием N1, и параметрического числа объекта, связанного условием N2.
Перпендикулярность прямой к плоскости
Прямая общего положения 4-х параметрическая. Прямая, перпендикулярная к плоскости, определяется точкой в плоскости, следовательно, 2-х параметрическая.
Точно такой же результат можно получить, если в качестве исследуемого объекта выбрать не прямую, а плоскость. Плоскость общего положения 3-х параметрическая. Плоскость, перпендикулярная к прямой, определяется точкой на прямой, следовательно однопараметрическая.
Перпендикулярность 2-х плоскостей
Плоскость общего положения 3-х параметрическая. Плоскость, перпендикулярная к заданной плоскости, определяется прямой в плоскости, следовательно 2-х параметрическая.
Перпендикулярность 2-х прямых (в плоскости)
Прямая общего положения 2-х параметрическая. Прямая, перпендикулярная к прямой, определяется точкой на прямой, следовательно, однопараметрическая.
Параллельность 2-х плоскостей
Плоскость общего положения 3-х параметрическая. Плоскость, параллельная к заданной, определяется текущей точкой на плоскости, следовательно, однопараметрическая.
Параллельность прямой и плоскости
Прямая общего положения 4-х параметрическая. Прямые, параллельные к заданной плоскости, находятся в параллельной к ней плоскости. Положение последней плоскости определяется текущей точкой в этой плоскости, т.е. одним параметром. В плоскости можно провести двухпараметрическое множество прямых. Следовательно, прямая, прямая, параллельная к плоскости, определяется 3 –я параметрами.
Параллельность 2-х прямых (в плоскости)
Прямая общего положения 2-х параметрическая. Прямая, ей параллельная, определяется текущей точкой на прямой, следовательно однопараметрическая.
Параллельность 2-х прямых (в пространстве)
Прямая общего положения 4-х параметрическая. Прямые, ей параллельные, перпендикулярны к одной и той же плоскости. Прямая, перпендикулярная к плоскости 2-х параметрическая, следовательно и прямая, параллельная к заданной прямой, тоже двухпараметрическая.
Касание 2-х линий (на плоскости)
Рассмотрим касание прямой и кривой. Прямая общего положения 2-х параметрическая. Через точку на гладкой кривой можно провести единственную касательную. Точка на линии определяется одним пара-метром, следовательно, и касательных к кривой можно провести однопараметрическое множество.
Касание 2-х линий (в пространстве)
Рассуждая по аналогии с предыдущим случаем, получим:
Касание 2-х поверхностей
Рассмотрим касание плоскости и поверхности. Плоскость общего положения 3-х параметрическая. Через точку на гладкой поверхности можно провести единственную касательную плоскость. Точка на поверхности определяется двумя параметрами, следовательно, и касательных поверхностей можно провести двухпараметрическое множество.
Касание линии к поверхности
Рассмотрим касание прямой к поверхности. Прямая общего положения 4-х параметрическая. Через точку на гладкой поверхности можно провести единственную касательную плоскость (определяется 2-я параметрами), а в ней, через ту же точку можно провести однопараметрическое множество прямых. Следовательно, прямых, касательных к поверхности можно провести 3-х параметрическое множество.
Симметрия
При условии явно или неявно заданных центра, оси или плоскости симметрии учитываются параметры только одной из двух симметричных точек. Следовательно, условие симметрии заменяет количество параметров, равное параметрическому числу лишь одной из симметричных частей.
Выделение параметров формы и положения
Практически все геометрические объекты характеризуются параметрами формы и положения. Исключение составляют точка, прямая и плоскость. Эти элементы различаются в пространстве только лишь положением. Параметры положения Nп и параметры формы Nф в сумме определяют общее параметрическое число N:
Число параметров положения зависит от размерности пространства. В общем случае Nп = 3 для объектов на плоскости и Nф = 6 для объектов в пространстве. Этот факт несложно доказать, используя приемы параметризации.
Для доказательства достаточно определить количество параметров, которых необходимо для определения положения одной декартовой системы координат относительно другой.
Определение параметров положения на плоскости
Система координат определяется:
• точкой (2 параметра);
• прямой, которая проходит через заданную точку и текущую точку линии (ещё один пара-метр);
• прямой, которая проходит через заданную точку перпендикулярно к заданной прямой (без параметров).
Определение параметров положения в пространстве
Система координат определяется:
• точкой (3 параметра);
• прямой, которая проходит через заданную точку и текущую точку линии (ещё 2 параметра);
• прямой, которая проходит через заданную точку, лежит в плоскости, перпендикулярной к заданной прямой, и проходит через текущую точку линии (1 параметр);
• прямой, которая проходит через заданную точку перпендикулярно к заданной плоскости (без параметров).
Всего 6 параметров.
Пример определения параметров формы и положения объектов
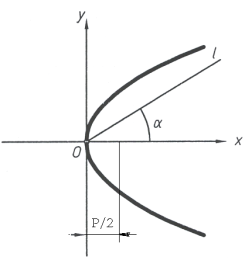
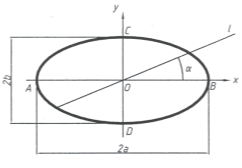
Эллипс – множество точек на плоскости, сумма расстояний от каждой из которых к 2-м точкам (фо-кусам) есть величина постоянная (больше, чем расстояние между фокусами).
Отделяем в определителе эллипса геометрическую часть от алгоритмической. Геометрическая часть состоит из 2-х фиксированных точек на плоскости и одной текущей точки на линии.
Выражаем элементы определителя через параметры
Определяем количество параметров формы и положения.
Nп = 3
Nф=N — Nп = 5 – 3 = 2
Определение множества решений геометрических задач
В теории алгоритмов одна из важных проблем – доказать отсутствие алгоритма для решения той или иной задачи. Доказать наличие алгоритма можно путем фактического описания процесса. Доказать же отсутствие алгоритма сложнее. То, что Вы его не сумели описать, отнюдь не означает, что алгоритм не существует. Приемы параметризации позволяют в некоторой степени решить эту проблему в отношении моделирования геометрических объектов.
Задача_1.
Провести прямую, которая пересекает 3 (4 или 5) заданных прямых.
Для того, чтобы оценить, какое множество решений имеет задача, необходимо определить:
1. Какая размерность множества прямых в трехмерном пространстве?
2. Какая размерность геометрического условия (определяется разницей параметрического числа объекта, несвязанного условием, и параметрического числа объекта, связанного условием)?
3. Сколько необходимо условий, чтобы получить нульмерное множество прямых?
Доказательство. В пространстве имеем 4-х параметрическое множество прямых. Если же прямая, пересекает какую-либо линию, то имеем 3-х параметрическое множество прямых, поскольку одна из 2-х точек определяется в 1-о мерном пространстве – на заданной линии. Размерность геометрического условия пересечения линий Ny = 4 — 3 = 1. Следовательно, чтобы получить 0-мерное множество прямых достаточно 4 условия пересечения прямой с линией.
Задача_2.
Провести прямую, которая пересекает 2 заданные прямые и параллельна к 2-м заданным плоскостям (докажите самостоятельно).
Задача_4.
Доказать теорему Польке (основная теорема аксонометрии), используя метод параметризации. Теорема впервые была сформулирована немецким геометром К. Польке (К. Pohlke) в 1860 (без доказательства). П. т. утверждает, что три отрезка произвольной длины, лежащих в одной плоскости и выходящих из одной точки под произвольными углами, представляют собой параллельную проекцию трёх равных и взаимно перпендикулярных отрезков, выходящих из одной точки в пространстве. На основании П. т. три произвольных отрезка, выходящих из одной точки на плоскости проекций, можно принять за изображение координатного трёхосника с одинаковыми масштабными отрезками на его осях.
Доказательство. Из 4-х заданных на плоскости точек выходят прямые линии (проецирующие лучи). Направление этих лучей определяется двумя параметрами (текущей точкой линии). Положение точек на заданных прямых определяется 4-я параметрами (4*1). Из 6 параметров (степеней свободы) три параметра связываются условиями равенства каждого из отрезков единице. Два параметра связывает условие перпендикулярности прямой плоскости (например, оси Z к плоскости XY). Один параметр связывает условие перпендикулярности 2-х прямых в плоскости (например, оси X и Y в плоскости XY).
Определение линий и поверхностей изменением размерности множеств
Можно уменьшать или увеличивать размерность множества за счёт высвобождения параметров или их связывания теми или иными геометрическими условиями. Так, например, от фиксированной точки можно последовательно перейти к текущим точкам линии и поверхности. И, наоборот, от поверхности можно перейти к линии и точке.
Поверхность можно определить как однопараметрическое множество линий, поскольку высвобождением одного параметра каждой из точек линии можно получить 2-х параметрическое множество точек. Например, если перемещать окружность вдоль оси, получим цилиндрическую поверхность.
С другой стороны, к определению поверхности можно перейти, накладывая определённые условия на N-параметрическое множество линий. Так, например, к определению поверхности можно прийти, накладывая на 4–х параметрическое множество прямых условие пересечения 3-х заданных прямых (каждое условие связывает один параметр).
Ниже напоминаются некоторые основные термины и положения из указанных источников [11] и [10].
Процессы конструирования изделий и формирования чертежей неразрывно связаны с геометрией. Для глубокого изучения этих процессов необходимо изучить эти связи, что облегчит формирование более точных представлений и продуктивной методики разработки конструкций.
Легко установить связи между терминами и понятиями, которые применяются в конструировании изделий, с одной стороны, и в геометрии, инженерной графике, теории параметризации фигур – с другой.
Понятие параметра отвечает понятию размера. Параметры могут так же, как и размеры, определять форму изделия (фигуры – в геометрии) либо положение изделия.
Понятие системы параметризации соответствует понятию системы баз, которое, в свою очередь, соответствует понятию системы координат [10].
Система параметризации (система баз) может быть выбрана независимо от параметризуемого изделия. В этом случае могут быть выделены параметры, определяющие положение изделия в пространстве, где заданы базы.
Система параметризации может быть выбрана в параметризуемом изделии в виде его элементов.
В таком случае могут быть выделены параметры, которые в этой системе баз определяют форму изделия.
На чертеже форма изделия может быть определена с точностью до подобия. В этом случае масштаб чертежа дополняет информацию о форме фигуры до ее величины.
Например, треугольник можно задать в виде изображения, задав одну сторону произвольной длины и два числовых параметра, показывающих отношения заданной стороны к незаданным сторонам. В этом случае треугольник на чертеже задается с точностью до подобия (то есть задается множество треугольников одной и той же формы, но не величины). Если теперь задать масштаб, в котором вычерчена первая из сторон, то выделяется единственный треугольник.
Таким образом, три параметра формы определяют единственный треугольник и по форме, и по величине.
Изображение фигуры на чертеже, лишенное размеров, может определять ее форму с точностью до подобия. Указание масштаба изображения позволяет восстановить параметры формы фигуры и величину фигуры.
Другой особенностью чертежа является игнорирование некоторых размеров (параметров), которые обслуживают известные в геометрии геометрические условия, возникающие между элементами фигуры на чертеже.
Примером является симметрия, которая позволяет сократить количество размеров на чертеже.
Широкое распространение в конструировании имеют геометрические условия взаимной перпендикулярности либо параллельности элементов изделия, которые проецируются на чертеже в виде соответствующих линий.
В таких случаях величины углов, равные 0 и 90°, не указываются в виде размерных чисел. Исключение составляют случаи, когда на эти величины накладываются требования определенной точности выполнения.
Во всех этих примерах работает наглядность чертежа. Соответствующие параметры определяются условностями чертежа или с помощью условных обозначений.
Рассмотрим еще одну особенность параметрического описания изделия с помощью чертежа и параметров, выявляемую на этапе применения чертежа изделия в условиях производства.
Возникает проблема переноса размеров с геометрической модели на физическое изделие. Известно, что любая операция измерения может быть выполнена только с некоторой степенью точности. Поэтому физическое изделие в определенной степени отличается от геометрической модели. Параметры формы и положения, заложенные в геометрическую модель, реализуются с ошибками измерения. Поверхности физической модели отличаются от идеальных поверхностей, заложенных в геометрической модели.
Указанные отклонения должны быть нормированы в каких-то пределах, иначе из деталей нельзя будет собрать изделие. Они будут отличаться друг от друга так, что их трудно будет ремонтировать. Проблема запасных частей станет трудноразрешимой, поскольку одна из таких частей будет отличаться от другой настолько, что ее нельзя будет применить без доработки.
Поскольку ошибки измерения существенно меньше по величине, чем измеряемые параметры, можно говорить о параметрическом подходе в геометрическом моделировании на «микроуровне». Чертежи, входящие в состав рабочей документации, отображают необходимое количество сведений об изделии.
Эти сведения могут быть отнесены к конструкторско-технологической информации.
Среди них сведения о материале, способе получения заготовок, о покрытиях поверхностей и их термообработках, о видах и способах обработки и т. д.
Часть сведений могут быть интерпретированы как геометрическая информация, характеризующая форму и положение частей изделия дополнительно к параметрам и условиям.
Вся информация, отображаемая на чертеже, изучается в полном объеме в специальных дисциплинах.
Дисциплина «Начертательная геометрия, инженерная графика» за счет внедрения параметрического подхода позволяет объединить весь геометрический материал единой теоретической базой.
При этом многие процессы, входящие в учебные программы, получают более точное алгоритмическое описание.
Задачи формирования чертежей, деталировка и чтение чертежа становятся более понятными. В связи с этим так называемые «учебные» чертежи приближаются к полноценным чертежам.