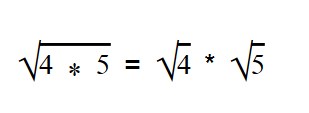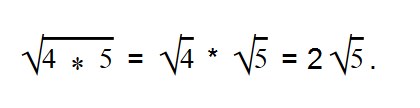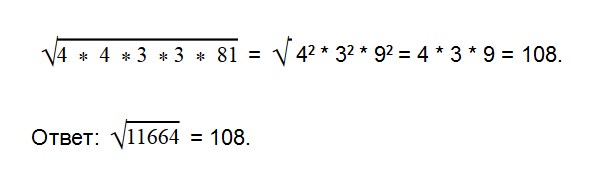Что такое перед числом
Свойства степеней. Действия со степенями
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
a — основание степени;
n — показатель степени.
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
2 — основание степени;
3 — показатель степени.
Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.
Задачка про миллион: представьте, что у вас есть миллион рублей. За один год вы заработали на нем еще два. Еще через год каждый миллион принес еще два и т. д. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
Математики заскучали и решили все упростить:
Ответ: через четыре года у вас будет 81 миллион.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени 2) и куб (показатель степени 3).
Определенный артикль в английском языке
Определенный артикль (the) сопровождает те существительные, которые уже должны быть известны слушателю из контекста, ситуации или из его общих знаний. Также он часто указывает на уникальные, единственные в своем роде предметы.
Определенный артикль в английском языке обладает двумя значениями: конкретизирующим и обобщающим.
Определенный артикль в конкретизирующем значении выделяет конкретный, отдельный предмет из объектов одного типа. Это выделение может осуществляться при помощи определения, контекста, ситуации или значения самого существительного:
Такие определения, как next, following, last, very и only, а также порядковые числительные конкретизируют существительное, поэтому оно должно использоваться с определенным артиклем:
Кроме этого, определенный артикль используется с прилагательными в превосходной степени:
Иногда английские прилагательные в превосходной степени могут использоваться и с неопределенным артиклем, тогда оно приобретает значение «весьма, крайне»:
Определенный артикль в обобщающем (родовом) значении относит предмет к целому классу предметов одного вида.
Если артикль имеет такое значение, то во множественном числе он опускается:
Определенный артикль в обобщающем значении также может использоваться с субстантивированными прилагательными (то есть перешедшими в класс существительных) и названиями социальных классов и различных направлений:
Также он может указывать на:
Определенный артикль во множественном числе
Английские существительные, которые в единственном числе используются с определенным артиклем, сохраняют его и во множественном числе:
Определенный артикль используется с существительными во множественном числе также, если имеются в виду все представители этой группы:
Кроме этого, определенный артикль может использоваться с сочетаниями существительных и количественных числительных, если они уже известны читателю:
Определенный артикль с именами собственными
Определенный артикль употребляется со следующими именами собственными:
The перед порядковыми и количественными числительными
Порядковые
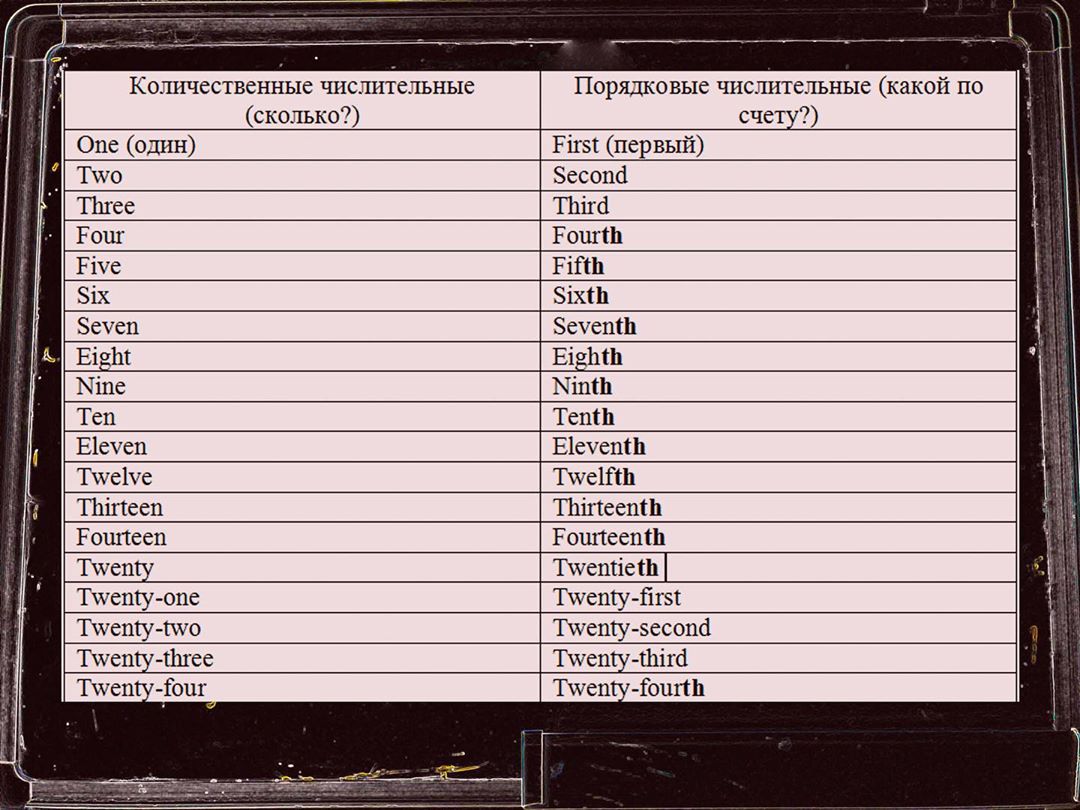
Порядковые числительные (Ordinals) обозначают порядок предметов при счёте и в русском языке отвечают на вопрос какой? (какая? какое? какие?), который? В английском языке порядковыми числительными являются first, second, third, fourth, fifth, sixth, seventh, eighth, ninth, tenth, eleventh, twelfth, thirteenth, fourteenth и т.д. Перед порядковыми числительными в английском языке обычно ставится определенный артикль the.
They met for the first time at the fireworks on the Fourth of July.
Они встретились впервые во время салюта четвертого июля.
Количественные
Количественные числительные (Cardinal numbers) обозначают количество или число. К количественными числительным относятся one, two, three, four, five, six, seven, eight, nine, ten, eleven, twelve, thirteen, foruteen и т.д. Обычно перед количественными числительными в английском языке не ставится никакой артикль. Однако существуют ситуации, когда мы должны ставить перед ними определенный артикль the. Когда в предложении говорится про конкретные два предмета, объекта, человека, но не выстраивают их в каком-либо порядке, то есть предметы равнозначны, но мы выделяем конкретно только эти.
Although their ideologies differ greatly, the two great powers must coexist.
Хотя их идеологии сильно различаются, две великие державы должны сосуществовать.
In 1808 Sir Humphry Davy stated the views of his generation very clearly: “if the two countries are at war, the men of science are not.”
В 1808 году сэр Хамфри Дэви очень четко изложил взгляды своего поколения: «если две страны воюют, то люди науки – нет.”
Что такое квадратный корень
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое квадратный корень
Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0
Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.
Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.
Попробуем найти корень из √-16
Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.
Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.
Числа, стоящие под знаком корня, должны быть положительными.
Исходя из определения, значение корня также не должно быть отрицательным.
Разница между квадратным корнем и арифметическим квадратным уравнением
Прежде всего, чтобы разграничить эти два понятия, запомните:
Это два нетождественных друг другу выражения.
Из выражения x 2 = 16 следует, что:
Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.
В то же самое время, из выражения x = √16 следует, что x = 4.
Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:
Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.
Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.
Даны два выражения:
Первое выражение — квадратное уравнение.
Второе выражение — арифметический квадратный корень.
Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.
Запись иррациональных чисел с помощью квадратного корня
Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.
Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.
Примеры иррациональных чисел:
Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.
Дано уравнение: x 2 = 2.
Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.
Переберем числа, чтобы удостовериться в этом:
1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.
Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.
Извлечение корней
Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.
Таблица квадратов
Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:
Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.
Ищем в таблице число 3025.
Влево — 5, вверх — 5.
Ищем в таблице число 7396.
Ищем в таблице число 9025.
Ищем в таблице число 1600.
Извлечением корня называется нахождение его значение.
Свойства арифметического квадратного корня
У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.
Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.
Умножение арифметических корней
Для умножения арифметических корней используйте формулу:
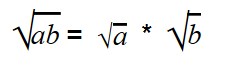 |
Примеры:
Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.
Если нет возможности извлечь корни из чисел, то поступаем так:
Деление арифметических корней
Для деления арифметических корней используйте формулу:
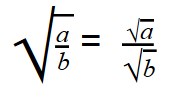 |
Примеры:
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.
Возведение арифметических корней в степень
Для возведения арифметического корня в степень используйте формулу:
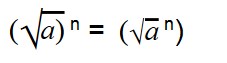 |
Примеры:
Эти две формулы нужно запомнить:
Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.
Внесение множителя под знак корня
Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.
А теперь давайте разберемся, как вносить множитель под знак корня.
Число семь умножено на квадратный корень из числа девять.
Извлечем квадратный корень и умножим его на 7.
В данном выражение число 7 — множитель. Давайте внесем его под знак корня.
Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.
Вы помните, что (√a) 2 = a
Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.
7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.
Формула внесения множителя под знак корня:
Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.
Вынесение множителя из-под знака корня
С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.
Дано выражение в виде квадратного корня из произведения.
Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.
Извлекаем корень из всех имеющихся множителей.
В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:
Таким образом множитель выносится из-под знака корня.
Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.
Раскладываем подкоренное выражение на множители 28 = 7*4.
Сравнение квадратных корней
Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.
Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.
Если:
Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.
Ответ: преобразовываем выражение 9√5.
9√5 = √81 * √5 = √81*5 = √405
Ответ: преобразовываем выражение 7√12.
7√12 = √49 * √12 = √49*12 = √588
Это значит, что 7√12 > √20.
Как видите, ничего сложного в сравнении арифметических квадратных корней нет.
Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.
Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.
Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.
Таких калькуляторов в интернете много, вот один из них.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
Мы видим что, 2116 больше 1600, но меньше 2500.
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.
Как пользоваться таблицей
4 2 = 16 ⇒ 6
5 2 = 25 ⇒ 5
6 2 = 36 ⇒ 6
7 2 = 49 ⇒ 9
8 2 = 64 ⇒ 4
9 2 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Далее вычисляем: 44 * 44 = 1936.
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
Запишем выражение в следующем виде:
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10
dressedbread.com
все об изучении английского языка
Артикль перед порядковыми числительными: the, a или нулевой?
Сегодня мы разберемся, какой необходимо ставить артикль перед порядковыми числительными: определенный (the), неопределенный (a/an) или нулевой.
Считаю должным напомнить, что для ежедневного английского необходимо умело орудовать двумя типами числительных: количественными (cardinal numerals: one, two, thirty-six) и порядковыми (ordinal numerals: the first, the second, the thirty-sixth). Если вдруг вы не понимаете, об чем это я толкую, то срочно себя спасайте (см. таблицу ниже).

МИФ: артикль перед порядковыми числительными должен быть всегда THE
Вполне возможно, что порядковые числительные у вас неразрывно связаны с артиклем THE. Например, this is THE FIRST book I’ve ever read или The Goblet of Fire is THE FOURTH installment in the Harry Potter movie series. Здесь все правильно.
Однако в этой статье мы рассмотрим восемь исключений из этого «правила». Вы увидите, что в зависимости от ситуации артикль перед порядковыми числительными может быть как неопределенный, так и нулевой.
Случаи, когда НЕ НУЖЕН артикль перед порядковыми числительными
1. Даты
Каждое школьное занятие помимо фразы who’s on duty today включало себя написание даты на доске: the 6th (sixth) of November. Это британский формат.
В американском варианте число и месяц меняются местами, опускается THE и получается такое: November, 6th.
а) занять первое место
take the first place
take/win first place, come in first, finish first
б) быть на втором месте
to be on the second place
to be IN second place
Хотите узнать, как я выучил более 15 000 английских слов, не покидая пределов родины? Читайте мою лучшую статью про то, как выстроить эффективную систему по увеличению словарного запаса.
3. Всякие рейтинги
In 2009, US teenagers ranked 26th on the PISA math test and 12th in reading.
Microsoft Founder Bill Gates came in first, Barack Obama in second place and actor Jackie Chan in third.
4. В каком вы классе?
«Мы в четвертом классе»
We’re in the fourth class.
We’re in fourth grade (AmE).
Иногда можно встретить постановку THE в данном случае, но только иногда.
Кстати, grade – не только «класс», но и «оценка» (см. эту статью).
5. Наречия
а) Let’s do that first, okay?
First = сначала.
б) First (во-первых), you don’t even know what you’re talking about and second (во-вторых), it’s time for you to listen to me.
в) When did you first meet each other?
First = for the first time.
г) Beth always arrives first at meetings.
Да, я понимаю, что в данном случае first переводится как прилагательное (приезжает какой? – первой), но в английском это наречие: arrives как? – first.
Случаи, когда нужно ставить неопределенный артикль перед порядковыми числительными
6. Порядковые числительные в значении «еще один»
I’m giving you a second chance (=one more chance, another chance).
«Еще один» – это, как правило, то, что не планировалось изначально; то, что не упоминалось или не подразумевалось. В таких случаях ставим артикль A.
Для запланированного, подразумеваемого или уже упомянутого мы используем THE.
Пример ниже превосходно иллюстрирует разницу между изначально незапланированными (a second time, a third attempt) и уже упомянутыми/подразумеваемыми попытками сдачи экзамена (the first attempt, the second attempt):
Of the 50 people who failed the first attempt, only 40 attempted the exam a second time; of the 24 who failed the second attempt, only 14 made a third attempt.
7. Треть, четверть, пятая часть, одна шестая и т.д.
a third (1/3) of the cake
a fourth (1/4) of the pizza
a tenth (1/10) of a percentage point
8. Комбинации составных прилагательных и существительных
Возьмем словосочетание third-world country. Будем ли мы «по правилу» ставить THE перед THIRD? Конечно же, нет. Здесь вообще другая ситуация.
THIRD-WORLD в данном словосочетании – прилагательное, определяющее слово COUNTRY.
Собственно, вместо third-world можно было бы поставить и big, и rich, и great, и the worst.
Разница в том, что в нашем примере прилагательное состоит из двух слов (third и world), одно из которых порядковое числительное.
Для правильной постановки артикля необходимо уметь отсекать шелуху из длинных прилагательных и находить главное (оно же определяемое) слово.
Cuba is a third-world country.
I’m a first year PhD student – здесь прилагательное уже трехсложное. И это не предел. Бывает и больше.
a seventh-day Adventist church – церковь адвентистов седьмого дня
a first-class passenger – пассажир первого класса
a first aid kit – аптечка
a second degree burn – ожог второй степени
В определенных контекстах возможна постановка THE, но отнюдь не из-за присутствия порядкового числительного. Вот вам пища для размышления =)

9. О сексе на английском: бейсбольные метафоры
Бонусный девятый случай, в котором не нужен артикль перед порядковыми числительными: эвфемизмы, описывающие этапы соблазнения.
В США для указания достигнутого уровня интимной близости могут использоваться бейсбольные термины:
get to first/second/third base и hit a homerun.
First base – поцелуи, homerun – половой акт.
В подробности second и third base вдаваться не вижу смысла. Думаю, вы сами легко разберетесь 😉