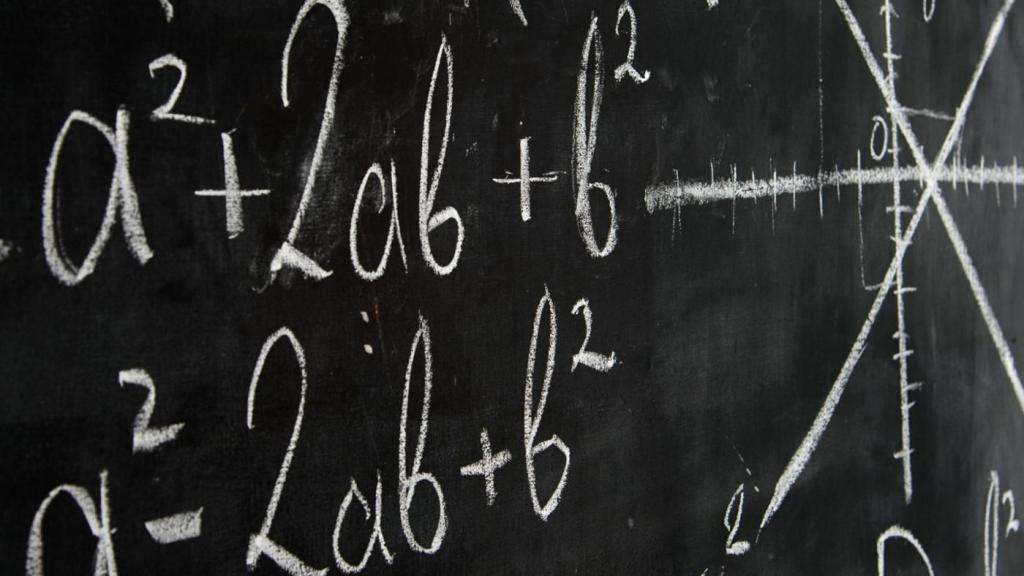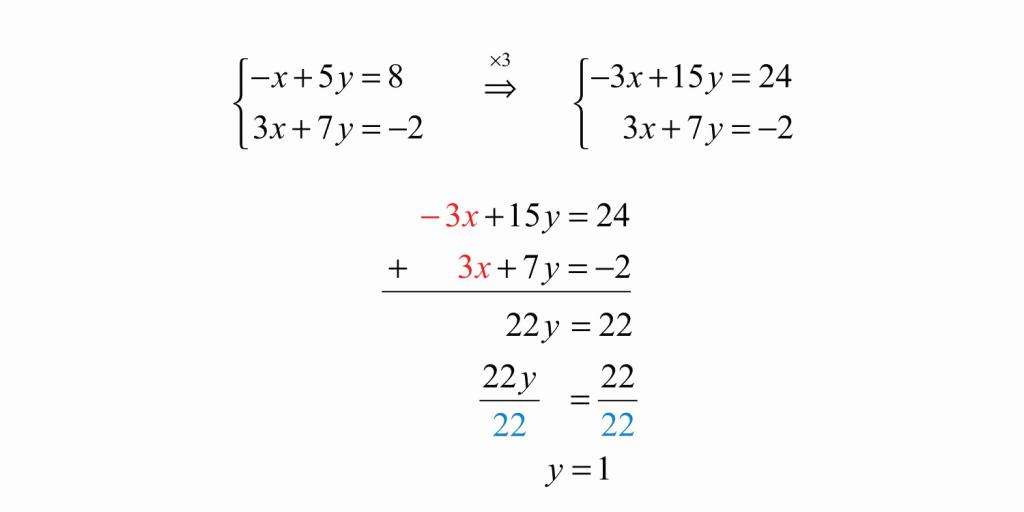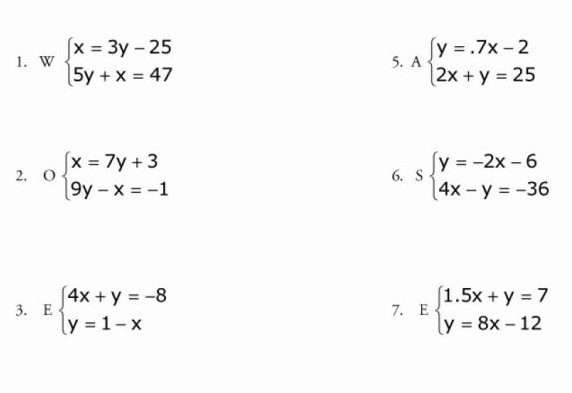Что такое переменные слагаемые
Что такое переменные? Переменная величина в математике
Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.
Понятие переменной

Виды величин

Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).
Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.
История
История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.
Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.
С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:
За x2 принимаем некое k, и уравнение приобретает понятный вид:
Вот какую пользу в математику несет введение переменных.
Неравенства, примеры решения
Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:
Пример с одной переменной:
Делим обе части неравенства на 10 и получаем:
Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.
Решением этого неравенства будет промежуток (20; +∞).
Решение нестрогого неравенства осуществляется так же, как и строгого:
Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.
Квадратные неравенства
Если взять квадратное уравнение вида ax2 + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.
Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.
По формуле корней квадратного уравнения получаем:
Или можно было решить это уравнение по теореме Виета:
Методом подбора получаем такие же корни уравнения.
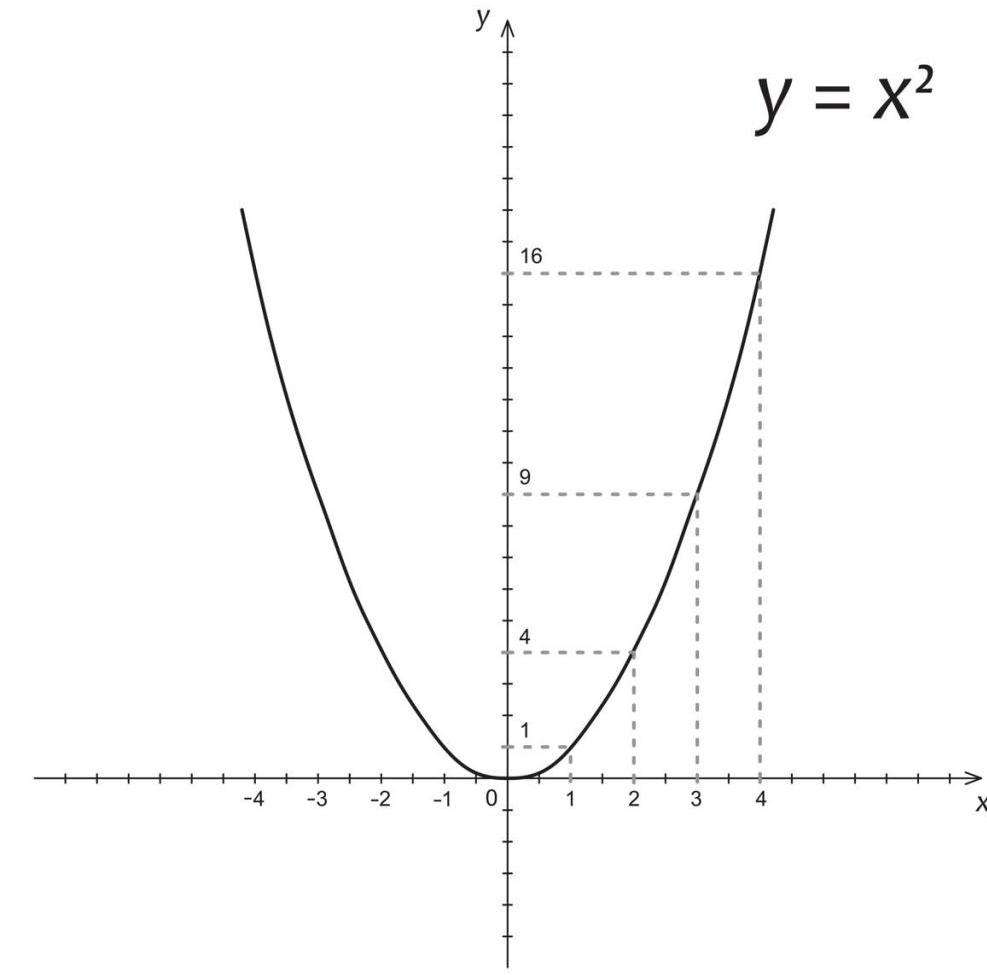
Парабола
1. Определяем, куда направлены ветви параболы.
2. Приравниваем функцию к нулю и находим корни уравнения.
3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.
Выписываем в виде функции:
Приравниваем к нулю.
Дальше решаем как квадратное уравнение и находим нули функции:
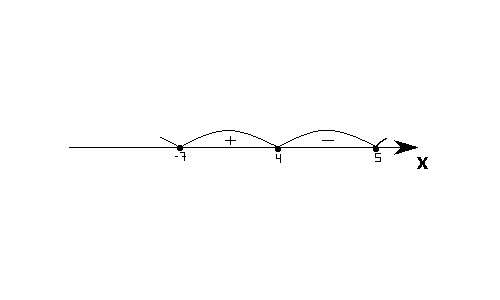
Метод интервалов
1. Находим корни уравнения, при которых неравенство равно нулю.
2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.
3. Определяем знак любого интервала.
4. Расставляем знаки у остальных интервалов, меняя их через один.
2) Изображаем их на числовой прямой.
3) Определяем знаки интервалов.
2. Отмечаем их на числовой прямой.
3. Определяем знаки интервалов.
Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.
Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.
Системы уравнений
Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.
Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.
Алгебраический метод
Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.
Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:
Решаем получившееся уравнение и находим икс.
Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:
Метод подстановки
Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.
В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:
Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:
Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:
2.4. Переменные
Рассмотрим такую задачу: «Денис старше Матвея на 2 года. Сколько лет будет Денису, когда Матвею будет 10 лет?» Решить ее можно следующим образом:
А интересно, сколько лет будет Денису, когда Матвею будет 11 лет? Решение в этом случае выглядит так:
А если Матвею будет 12 лет? — Тогда так:
Спрашивается, нельзя ли как-нибудь на все подобные вопросы ответить раз и навсегда в виде какого-нибудь правила? Оказывается можно:
(возраст Дениса) = (возраст Матвея) + 2.
Правила, записанные в виде равенств, называются формулами. Математикам очень часто приходится исписывать целые страницы разными равенствами и формулами, поэтому они стремятся делать их, по возможности, краткими. Математик предпочел бы написать следующим образом:
а потом отдельно пояснить, что Д означает возраст Дениса, а М — возраст Матвея. Но и это не принесло бы ему полного удовлетворения. Математики предпочитают пользоваться буквами самого распространенного в мире алфавита — латинского. Вот запись, которая удовлетворила бы математика полностью:
Разумеется, как и ранее, к этой формуле необходимо еще приложить пояснения, что d — это возраст Дениса, а m — это возраст Матвея.
Итак, скажите мне, сколько лет Матвею, — и, глядя на эту формулу, я вам быстро отвечу, сколько лет Денису. Принято говорить: если m принимает значение 10, то d принимает значение 12. Или: если m = 10, то d = 12. Буквы, которые входят в математические выражения и которые могут принимать разные численные значения, называются переменными.
Мы уже довольно давно занимаемся математикой и успели за это время сделать кое-какие важные математические открытия. С помощью формул мы можем теперь эти открытия грамотно записать. Например, мы однажды заметили, что если поменять местами слагаемые, то значение суммы не изменится. В виде формулы это записывается следующим образом:
где a и b — любые числа. Школьные учителя называют это «перестановочным свойством сложения». Лично мне такое словосочетание режет слух. Это примерно то же самое, что сказать: «оранжевое свойство апельсина». Перестановочным является, конечно, не свойство, а само сложение. А профессиональные математики используют тут и вовсе другое слово. Они говорят: сложение коммутативно.
Равенства, которые остаются верными при любых значениях входящих в них переменных, называются тождествами. Вот еще пример тождества:
или, что то же самое,
Это знакомое нам правило, по которому можно изменять порядок действий, или, как мы еще говорили, раскрывать скобки. У школьных учителей это называется «сочетательным свойством сложения». Грамотные же люди говорят: сложение ассоциативно.
Но, разумеется, не всякое равенство является тождеством. Зададимся вопросом: коммутативно ли вычитание? Можно ли написать так:
Ну, написать-то так, пожалуй, можно: бумага, говорят, все вытерпит. Но вычитание, конечно же, некоммутативно, а значит, данное равенство не является тождеством. Убедиться в этом очень просто. Пусть, например, a = 2 и b = 1. Подставляем эти значения в равенство и получаем: «2 − 1 = 1 − 2». Ерунда какая-то! Но, с другой стороны, пусть a = 5 и b = 5. В этом случае равенство принимает вид: «5 − 5 = 5 − 5». Ну, что ж, спорить нечего, так оно и есть. Равенство, которые становятся верными лишь при некоторых значениях переменных, называются уравнениями.
Уравнениями очень удобно пользоваться при решении всевозможных математических задач. Вернемся к задаче про Дениса и Матвея: «Денис старше Матвея на 2 года. Каков будет возраст Дениса, d, когда Матвею будет m лет?» Мы твердо знаем, что Денис всегда останется старше Матвея на одно и то же число лет (такие неизменные величины называются инвариантами). Поэтому мы можем составить следующее уравнение:
Здесь две переменные, а именно d и m. Следует отметить, что роль этих переменных неодинакова. Предполагается, что численное значение переменной m нам известно. Если даже мы не знаем этого значения сейчас, то, вероятно, нам назовут его когда-нибудь потом. И уж, во всяком случае, его нахождение не входит в нашу задачу. Такие переменные называются параметрами. В противоположность этому, о численном значении переменной d нам никто никогда не собирается сообщать. Наша задача как раз и заключается в том, чтобы его найти. Такие переменные называются неизвестными.
Решить уравнение — это значит выписать формулу, по которой можно вычислить значение неизвестной, если нам скажут численное значение параметра. В данном случае решение — это
Давайте посмотрим, как мы пришли от исходного уравнения
к его решению. Ну, мы пристально посмотрели на уравнение, что-то прикинули в уме и выписали результат. Так делать, конечно, можно. Однако в математике разработаны особые методы, которые позволяют решать уравнения без особенного умственного напряжения. Тут очень удобно воспользоваться одним простеньким приемом.
Но сперва — небольшое отступление. Допустим, у Дениса в брюках есть два кармана, один слева, другой справа. В этих карманах лежат конфеты. Точное количество конфет нам неизвестно, но мы знаем, что в левом и правом карманах конфет поровну. Введем обозначения. Пусть L — это число конфет в левом кармане, а P — это число конфет в правом кармане. На основе имеющихся у нас сведений, мы можем составить уравнение:
Далее события развиваются так. Денис положил в левый карман еще одну конфету и в правый карман еще одну конфету. Ясно, что в обоих карманах конфет снова оказалось поровну:
А что было бы, если бы Денис положил в каждый карман не по одной конфете, а по двум или трем или десяти? Ну, наши рассуждения тогда не сильно бы изменились. Просто в новом уравнении вместо «1» мы написали бы «2» или «3» или «10». Рассмотрим ситуацию, как говорят математики, в общем виде. Пусть Денис положил в каждый карман по k конфет. В обоих карманах конфет как было, так и осталось поровну. Значит,
Заметим, что параметр k может даже быть отрицательным (то есть Денис не кладет конфеты, а, наоборот, берет их).
Тут напрашивается очень важный вывод. Оказывается, что если у нас есть какое-то уравнение, то к обеим его частям можно одновременно прибавить одно и то же число, и тогда уравнение, по своей сути, не изменится. Если при каких-то значениях переменных первое уравнение обращается в верное равенство, то при тех же самых значениях переменных обратится в верное равенство и второе уравнение. И наоборот, если обратилось в верное равенство второе уравнение, то и с первым уравнением случилось то же самое. Иными словами, оба уравнения имеют одинаковые решения. Профессиональные математики в этом случае говорят, что уравнения эквивалентны.
Вернемся теперь к задаче про возраст Дениса и Матвея. Мы получили уравнение
Прибавим теперь к обеим его частям параметр m:
После очевидных упрощений новое уравнение принимает вид:
Вот и всё! Решение получено.
Рассмотрим теперь другую, но очень похожую задачу, в которой вопрос поставлен несколько по-другому: «Денис старше Матвея на 2 года. Каков будет возраст Матвея, m, когда Денису будет d лет?» Уравнение, которое можно составить по условию, оказывается по виду точно таким же, как и прежде:
Однако, на этот раз, переменная d является параметром, а переменная m — неизвестной. В таких случаях еще говорят, что уравнение требуется решить относительно переменной m. Такое решение находится лишь ненамного труднее предыдущего. Прибавим к обеим его частям вначале m, а потом (− 2):
После упрощений получаем:
Тут стоит обратить внимание вот на что. В исходном уравнении переменная m была в левой части, и перед ней стоял знак минус. В конечном уравнении эта же переменная находится в правой части, и подразумевается, что перед ней стоит знак плюс. Говорят, что слагаемые в уравнениях можно переносить из одной части в другую с противоположным знаком (то есть минус следует менять на плюс, а плюс — на минус). В данном случае, справедливость этого правила можно также проследить на числе 2. Вначале двойка стояла справа, и перед ней подразумевался знак плюс. А в конце она оказалась слева со знаком минус.
Теперь вспомним о задаче, которую мы решаем. В полученном уравнении осталось только поменять местами левую и правую часть — и ответ готов:
После того, как уравнение решено, полезно сделать так называемую проверку, то есть подставить найденное решение в исходное уравнение и посмотреть, что получится. Например, в данном случае, в исходном уравнении,
надо m заменить на (d − 2):
И что же получилось? Ну, конечно, тождество! Если бы мы не получили тождества, это бы означало, что уравнение решено неверно.
Подобные же рассуждения применимы и к неравенствам. Рассмотрим, для примера, такую задачу. Сколько лет должно пройти, чтобы Матвею можно было официально смотреть фильмы для взрослых? Поскольку человек считается взрослым с 18-ти лет, мы должны записать:
где m обозначает нынешний возраст Матвея, а x — это число лет, которые ему надо подождать, чтобы его стали пускать в кинотеатр на сеансы для взрослых. Значок «≥» у математиков заменяет слова «больше или равно». Ясно, что если прибавить (или отнять) от обеих частей неравенства одно и то же число, то оно оcтанется по сути тем же самым. Или, говоря точнее, оно превратится в эквивалентное неравенство, которое имеет в точности то же самое решение, что и первоначальное. Отнимаем от обеих частей нашего неравенства число m и получаем:
Если Матвею сейчас, допустим, 12 лет, то
Таким образом, для того чтобы Матвей мог официально смотреть фильмы для взрослых, должно пройти 6 лет или больше.
Точно так же, нам может приготиться понятие «меньше или равно», которые обозначается значком «≤». Допустим, мы в составе группы из a человек дожидаемся лифта в многоэтажном доме. Грузоподъемность лифта ограничена 12-тью человеками, но, когда он подойдет, может оказаться, что в нем уже есть x человек. Спрашивается, каково должно быть значение x, чтобы вся наша группа зараз поместилась в лифте? Записываем:
и, применив наш обычный трюк, получаем:
Отметим заодно, что вся эта задача имеет смысл, только если численность нашей группы меньше или равна 12-ти человек:
Посмотрим теперь, как ведут себя переменные в примерах на умножение и деление. Пусть требуется найти неизвестную переменную x в уравнении:
По условию нашей задачи, x/3 и 4 — это одно и то же число, просто записанное двумя разными способами. Умножим-ка мы это число на 3. И результат тоже запишем по-разному:
После несложных вычислений получаем:
Решение уравнения найдено.
А теперь сможем ли мы решить такое уравнение (опять-таки относительно x)?
После деления обеих частей этого уравнения на 5 получаем:
А как насчет такого уравнения?
Это уравнение решается в два действия. Вначале умножаем обе его части на x:
А потом делим на 3:
Теперь остается только для большей красоты поменять местами левую и правую части этого равенства:
И решение окончательно готово.
Если после всего этого нам встретится неравенство с неизвестным, такое, например, как
то мы, конечно, не растеряемся и тоже сможем легко найти его решение, потому что оно находится с помощью всё тех же самых трюков, что и в случае уравнений. Впрочем, тут надо сделать одну важную оговорку. Хотя мы уже и познакомились с отрицательными числами, умножением и делением на них мы пока еще не занимались. Покуда мы делим и умножаем только на положительные числа, все рассмотренные тут трюки прекрасно работают в одинаковой степени как для равенств, так и для неравенств. Но когда мы перейдем к умножению и делению на отрицательные числа, тогда у неравенств обнаружатся кое-какие особенности, о которых мы будем еще говорить отдельно. Что же касается умножения и деления на ноль, то, как мы знаем, делить на ноль вообще нельзя, а умножать на ноль обе части равенств или неравенств не имеет смысла, потому что при умножении любого числа на ноль получается ноль. Если в обеих частях уравнения или неравенства у нас окажутся нули, то толку от этого ровным счетом никакого не будет.
2.4.1. Определить, какие из следующих равенств являются тождествами, а какие — уравнениями. Особо отметить уравнения, не имеющие решений (то есть такие равенства, которые не становятся верными ни при каких значениях переменных).
2.4.2. Для каждого выражения из левого столбца найти тождественное выражение из правого столбца. (Два выражения называются тождественными, если при постановке между ними знака равенства получается тождество.)
Что такое переменная величина в математике
Содержание статьи
Переменные
Основным показателем переменной является то, что она записывается не числом, а буквой. Под условным обозначением чаще всего скрывается определенное значение. Переменная получила свое название благодаря тому, что ее значение меняется в зависимости от уравнения. Как правило, любая буква алфавита может быть использована в качестве обозначения для такого элемента. Например, если вы знаете, что у вас есть 5 рублей и вы хотите купить яблоки, которые стоят 35 копеек, конечное количество яблок, которые можно купить, обозначается буквой (например «С»).
Пример использования
Если есть переменная, которая была выбрана по вашему усмотрению, необходимо составить алгебраическое уравнение. Оно будет связывать между собой известные и неизвестные величины, а также показывать связь между ними. Это выражение будет включать в себя цифры, переменные и одну алгебраическую операцию. Важно отметить, что выражение будет содержать знак равенства.
Полное уравнение содержит значение выражения в целом. Оно отделено от остального уравнения знаком равенства. В предыдущем примере с яблоками 0.35 или 35 копеек, умноженные на «С», является выражением. Для того чтобы создать полное уравнение, необходимо записать следующее:
Мономиальные выражения
Полиномы
Зависимые и независимые переменные
В математике независимыми переменными являются неизвестные, которые определяют другие части уравнения. Они стоят отдельно в выражениях и не изменяются вместе с другими переменными.
Значения зависимых переменных определяются с помощью независимых. Их значения зачастую определяются эмпирически.
Число, переменная, функция
Вы будете перенаправлены на Автор24
Множество помогает понять, что такое «число».
Не все понятия в математике вводятся с помощью определений. Некоторые из них считаются основными, первичными и поэтому относятся к неопределяемым. Смысл таких понятий можно только объяснить с помощью примеров и описанием свойств. Общеизвестным из них является «точка». К таким же понятиям относится «множество».
Начальное представление о множестве можно получить, если рассмотреть совокупность произвольных объектов. Объекты в составе совокупности могут быть либо абстрактными (слова, числа, экзаменационные оценки), либо реальными (дома в городе, домашние вещи, товары в магазине, учащиеся в группе).
Первое отличие множества от совокупности. Объекты множества обязательно должны отличаться между собой. В то же время от объектов совокупности этого не требуется. Можно утверждать, что любое множество представляет собой совокупность, но не всякая совокупность может считаться множеством. Например, совокупность оценок, полученных группой студентов во время экзамена, состоит из многих «пятёрок», «четвёрок», «троек» и «двоек». Но ко множеству оценок принадлежат только четыре названных.
Второе отличие множества от совокупности. Объекты множества отличаются не только между собой, но и от объектов, которые в состав множества не входят. Например, все экзаменационные оценки, независимо от того, какими группами студентов они получены, принадлежат одному и тому же множеству. В то же время, оценки, полученные в разных группах, относятся к разным совокупностям.
Готовые работы на аналогичную тему
Существуют следующие варианты сравнения множеств:
Число
В математике используют множества, элементами которых являются числа. К стандартным числовым множествам относятся:
Основное свойство рациональных чисел состоит в том, что их всегда можно представить в виде десятичных дробей (конечных или бесконечных периодических).
Математически доказано, что рациональные числа не обеспечивают потребностей измерения величин. Например, диагональ квадрата со сторонами, равными единице, не может быть выражена рациональним числом. Именно поэтому были введены иррациональные числа.
Иррациональные числа записывают в виде бесконечных, но непериодических десятичных дробей.
Переменная
Общеизвестно, что при изучении явлений природы и при решении технических задач постоянно возникает необходимость рассматривать изменения числовых значених тех или иных величин. Более того, в математике могут изучаться изменения числовых значений неких абстрактных величин, не относящихся непосредственно к реальному миру.
В связи с этим возникла необходимость в использовании понятия «переменная величина».
В общем случае под переменной понимают каждый элемент некоторого числового множества. При этом некоторый фиксированный элемент этого множества называют значением переменной. Само же множество в этом случае называют областью значений переменной.
Чаще всего переменные обозначают буквами латинского или греческого алфавита.
Функция
В научных исследованиях, при решении практических задач всегда рассматривают изменения одних величин в зависимости от изменений других. Например, в электрической цепи величина тока меняется в зависимости от величины сопротивления, объем шара меняется в зависимости от его радиуса и т.д.
При этом в различных физических явлениях те или иные величины могут вести себя по-разному. Например, пр равномерном движении пройденное расстояние меняется в зависимости от времени, а скорость остается постоянной. А вот при равноускоренном движении в зависимости от времени меняется не только расстояние, но и скорость.
Взаимосвязь изменяемых величин в математике описывают с помощью функций.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 24 11 2021