Что такое переменные в физике

Переменная величина

Переме́нная — атрибут физической или абстрактной системы, который может изменять своё значение. Значение может меняться в зависимости от контекста, в котором рассматривается система, или в случае уточнения, о какой конкретно системе идёт речь. Концепция переменной широко используется в таких областях как математика, естественные науки, техника и программирование. Примерами переменных могут служить температура воздуха, параметр функции и многое другое. В широком смысле, переменная характеризуется лишь множеством значений, которые она может принимать.

Содержание

Переменные в математике

В математике переменная — это величина, характеризующаяся множеством значений, которое она может принимать. [1] При этом может иметься в виду как реальная физическая величина, временно рассматриваемая в отрыве от своего физического контекста, так и некая абстрактная величина, не имеющая никаких аналогов в реальном мире. В математическом анализе и большинстве смежных разделов математики под «переменной» обычно понимают численную величину, множество принимаемых значений которой включено в множество вещественных чисел.

Множество всех значений, которые может принимать данная переменная, называется областью изменения этой переменной. Это множество и задаёт переменную, то есть формально и является ей.

При моделировании переменные необходимо отличать от параметров, несмотря на то что переменная в одном контексте может быть параметром в другом.

В прикладной статистике переменная — оценочный фактор, или характеристика, или индивидуальный или системный атрибут. Иными словами, нечто, изменение чего ожидается с течением времени или между отдельными лицами.

Обозначения

Нужно отметить, что аналогичным образом обозначаются неизвестные в уравнениях, неравенствах и других подобных задачах. Например, . В этом случае имеются ввиду не переменные, хотя понятия весьма схожи и зависят от контекста.

Суть этого различия между неизвестной и переменной можно пояснить так. Запись можно, с одной стороны, трактовать как утверждение о свойстве неизвестной (в момент высказывания утверждения) величины , значение которой можно найти (или уточнить), отталкиваясь от приведенного утверждения как от исходной посылки. В этом случае будет обозначением конкретной, но до проведения выкладок (например, решения уравнения) неизвестной величины. С другой стороны запись можно трактовать как предикат, принимающий значение «истина» при одних значениях, подставляемых на место , и значение «ложь» при других. В этом случае является обозначением места в выражении, на которое могут подставляться различные (переменные) значения с целью определения логического (булева) значения записанного предиката. В этом случае правильнее рассматривать как переменную.

Переменные в программировании

В программировании переменная — это идентификатор, определяющий данные. Обычно это бывает имя, скрывающее за собой область памяти с хранящимися там данными. Переменная может иметь тип, характеризующий множество значений, которые она может принимать. В программировании, переменные, как правило, обозначаются одним или несколькими словами или символами, такими, как «time», «x», «foo» и тому подобное.

Следует отметить, что это значение в некотором смысле схоже с математическим. Математики в XVII веке придумали переменную именно для того, чтобы «забронировать» в формуле место, на которое в нужный момент можно подставить конкретное значение. Бумага в этом процессе является памятью, а обозначения (чаще, буквы) резервируют и именуют области этой памяти. Ощущение неоднозначности возникает из-за того, что формула в математике играет двоякую роль: если это алгоритм вычисления, смысл совпадает с программистским определением; если же формула визуализирует отношения своих элементов, мы абстрагируемся от роли переменной, как ячейки памяти, такое понимание теряет смысл.

Переменные в физике

В физике переменная — это некоторый атрибут модели реального физического процесса, принимающий количественные значения, физическая величина. Множество значений, которые может принимать конкретная переменная, определяется из физических соображений. Физические переменные связываются друг с другом физическими законами, в результате чего получаются математические модели различной степени сложности. Переменные в физике, как правило, кроме количественного значения характеризуются также размерностью.

Источник

Переменная величина

Переменная характеризуется только множеством значений, которые она может принимать. Переменную обозначают символом, общим для каждого из её значений.

Русский термин «переменная величина» происходит от латинской формулировки quantitas variabilis, также как в русском языке сокращаемой до единственного слова variabilis.

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

В теории вероятностей случайная величина имеет дискретное равномерное распределение, если она принимает конечное число значений с равными вероятностями.

В математике (особенно в теории категорий), коммутативная диаграмма — изображаемая в наглядном виде структура наподобие графа, вершинами которой служат объекты определённой категории, а рёбрами — морфизмы. Коммутативность означает, что для любых выбранных начального и конечного объекта для соединяющих их ориентированных путей композиция соответствующих пути морфизмов не будет зависеть от выбора пути.

Измери́мые функции представляют естественный класс функций, связывающих пространства с выделенными алгебрами множеств, в частности измеримыми пространствами.

Конечная разность — математический термин, широко применяющийся в методах вычисления при интерполировании.

Прострáнством называется математическое множество, имеющее структуру, определяемую аксиоматикой свойств его элементов (например, точек в геометрии, векторов в линейной алгебре, событий в теории вероятностей и так далее).Подмножество пространства называется «подпространством», если структура пространства индуцирует на этом подмножестве структуру такого же типа (точное определение зависит от типа пространства).

В логике логи́ческими опера́циями называют действия, вследствие которых порождаются новые понятия, с использованием уже существующих. В более узком смысле, понятие логической операции используется в математической логике и программировании.

Источник

Динамическая переменная (физика)

Динамические переменные описывают динамику системы в отличие от величин, характеризующих систему саму по себе, таких как масса. К динамическим переменным в механике относятся координаты, импульсы и функции от них. В других областях физики могут использоваться и другие динамические переменные, например, функции поля в квантовой теории поля. Важную роль в физике играют динамические инварианты (интегралы движения) — такие динамические переменные, которые сохраняют своё значение при эволюции системы.

В квантовой механике каждой динамической переменной сопоставляется линейный эрмитов оператор. Собственные значения этого оператора определяют возможные значения, которые может принимать данная физическая величина. Среднее значение оператора по заданному состоянию » border=»0″ /> предсказывает результат измерения физической величины. Операторы различных физических величин, вообще говоря, не коммутируют друг с другом. Следствием этого является принцип неопределённости: две некоммутирующие физические величины не могут быть одновременно измерены со сколь угодно высокой точностью.

См. также

Литература

Полезное

Смотреть что такое «Динамическая переменная (физика)» в других словарях:

Динамическая переменная — Динамическая переменная термин. Динамическая переменная (программирование) Динамическая переменная (физика) … Википедия

Гравитация с массивным гравитоном — название класса теорий гравитации, в которых частица переносчик взаимодействия (гравитон) предполагается массивной, примером является релятивистская теория гравитации. Характерная особенность таких теорий проблема разрыва ван Дама Вельтмана… … Википедия

Атмосфера Земли — (от греч. atmos ‒ пар и sphaira ‒ шар), газовая оболочка, окружающая Землю. А. принято считать ту область вокруг Земли, в которой газовая среда вращается вместе с Землёй как единое целое. Масса А. составляет около 5,15 1015 т. А. обеспечивает… … Большая советская энциклопедия

Атмосфера — I Атмосфера Земли (от греч. atmos пар и sphaira шар), газовая оболочка, окружающая Землю. А. принято считать ту область вокруг Земли, в которой газовая среда вращается вместе с Землёй как единое целое. Масса А. составляет около 5,15 1015… … Большая советская энциклопедия

ФЕРРОМАГНИТНЫЙ РЕЗОНАНС — резонансное поглощение эл. магн. энергии ферромагнетиком, один из видов электронного магнитного резонанса в твёрдом теле. От электронного парамагнитного резонанса (ЭПР) Ф. р. отличается тем, что поглощение энергии при Ф. р. на много порядков… … Физическая энциклопедия

Список обозначений в физике — Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия

Источник

Постоянный и переменный токи

Мы завершаем изучение темы «Постоянный электрический ток». Тем не менее, в этом параграфе мы рассмотрим и переменный ток. С чем это связано? Причина в самих терминах «постоянный ток» и «переменный ток», названия которых не вполне удачны, поскольку могут трактоваться по-разному в физике и электротехнике: так сложилось исторически. Обратимся к определениям.

В физике постоянным током называют электрический ток, не изменяющийся по силе и направлению с течением времени. Графиком такого «истинно постоянного» тока должна быть прямая, параллельная оси времени (см. рис. «а»). Тем не менее, в электротехнике постоянным током считают ток, который постоянен только по направлению, но может меняться по силе. Такой ток можно получить «выпрямлением» синусоидального переменного тока, например, того, который существует в домашней осветительной сети (см. рис. «б»). В результате получается пульсирующий однонаправленный ток (см. рис. «в»).

В физике переменным током называют электрический ток, изменяющийся с течением времени: по силе и/или направлению. С точки зрения физики, «пульсирующий» ток на рисунке «в» является переменным, поскольку меняется по силе (оставаясь постоянным по направлению). Такой однонаправленный ток в электротехнике считают «постоянным», так как по своим действиям он похож на настоящий постоянный ток. Например, он будет пригоден для зарядки аккумуляторов, работы электродвигателей, проведения электролиза. Переменный по направлению ток для этих целей непригоден.

Примечание. Почему ток в электрических сетях является именно синусоидальным и меняет своё направление 100 раз в секунду, мы расскажем позднее (см. § 10-ж). А пока рассмотрим, как из него можно получить однонаправленный пульсирующий ток – «постоянный» с точки зрения электротехники. Другими словами, как «перебросить» нижние части синусоиды вверх, то есть преобразовать форму тока без потери мощности этого тока? Для этого служат различные приборы, один из которых – полупроводниковый диод, пропускающий через себя ток лишь в одном направлении (см. § 09-и).

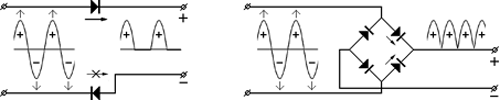
Ниже на левой схеме показано включение двух диодов в цепь переменного тока. При этом верхние части синусоиды проходят через верхний диод (по направлению его «стрелочки»), а нижние части синусоиды не проходят через нижний диод (против его «стрелочки»). Таким образом получается пульсирующий однонаправленный ток, и ровно половина исходной мощности не попадает к потребителю, так как образуются «равнины» с нулевым значением силы тока. Для особо интересующихся физикой заметим, что точно такой же результат будет, если оставить только один диод, причём, любой.

На правой схеме показано включение четырёх диодов по так называемой мостовой схеме. Она более выигрышна по сравнению с предыдущей: диоды попарно пропускают как верхние, так и нижние части синусоиды соответственно к клеммам «+» и «–». В результате из исходного переменного тока, на графике кторого можно условно выделить «холмы и овраги», на графике получающегося однонаправленного тока образуются «не холмы и равнины», а «удвоенные холмы». Это означает, что теперь к потребителю попадает вся мощность исходного тока.

И в заключение рассмотрим, как к непостоянному току можно применить закон Джоуля-Ленца Q=I²Rt, описывающий тепловое действие тока. Как быть, если сила тока постоянно меняется? Нужно её заменить на условно-постоянную силу тока, которая производит такое же тепловое действие. Такое условно-постоянное значение силы тока в физике называют эквивалентным (эффективным, действующим) значением силы непостоянного тока.

Определение: эквивалентное значение непостоянного тока равно значению такого постоянного тока, который, проходя через то же сопротивление, выделяет в нём то же количество теплоты за то же время. Именно эквивалентное значение тока показывают нам все амперметры. Аналогично и по отношению к напряжению и вольтметрам. Итак, определить эквивалентные значения непостоянных токов позволяют калориметрические измерения (см. § 06-в).

Источник

Переменная

Переменное, одно из основных понятий математики и логики. Начиная с работ П. Ферма, Р. Декарта, И. Ньютона, Г. В. Лейбница и др. основоположников «высшей» математики под П. понимали некоторую «величину», которая может «изменяться», принимая в процессе этого изменения различные «значения». Тем самым П. противопоставлялись «постоянным» (или константам) — числам или каким-либо др. «величинам», каждая из которых имеет единственное, вполне определённое значение (см. Переменные и постоянные величины). По мере развития математики и в ходе её обоснования представления о «процессах», «изменении величин» и т. п. тщательно изгонялись из математического арсенала как «внематематические», в результате чего П. стала пониматься как обозначение для произвольного элемента рассматриваемой предметной области (например, области натуральных чисел или действительных чисел), то есть как родовое имя всей этой области (в отличие от констант — «собственных имён» для чисел или др. конкретных предметов рассматриваемой области). Этот пересмотр взглядов на понятие П. был тесно связан с перестройкой математики на базе множеств теории (См. Множеств теория), завершившейся в конце 19 в. При всей простоте и «естественности» такой перестройки она существенным образом опирается на так называемую абстракцию актуальной бесконечности, позволяющую рассматривать произвольные бесконечные множества в качестве «данных» («завершенных», «готовых», «актуальных») объектов и применять по отношению к ним любые средства классической логики, отвлекаясь от незавершённости и принципиальной незавершимости процесса образования такого множества. Трудности решения логических проблем, связанных с принятием этой абстракции, делают понятной частичную «реабилитацию» старинных представлений о «переменных величинах»; при построении математических теорий представители некоторых школ (см. Математический интуиционизм, Конструктивное направление) предпочитают обходиться боле (слабой, но зато менее уязвимой в логическом отношении абстракцией потенциальной осуществимости, с точки зрения которой с бесконечными множествами как раз связываются представления о процессах их «порождения»,— сколь угодно далеко заходящих, но никогда не завершающихся (см. Бесконечность в математике). При исследовании вопроса непротиворечивости (См. Непротиворечивость) различных областей математики на такую позицию фактически встаёт значительное большинство математиков и логиков (см. Метаматематика).

В формализованных языках (исчислениях (См. Исчисление), формальных системах) математической логики П. называются символы строго фиксированного вида, могущие при определённых условиях заменяться выражениям данного исчисления. Это относится к так называемым свободным (или значащим) П. примером которых может служить П. в неравенстве х > 5, обращающемся при подстановке вместо х, скажем, цифры 7 (то есть обозначения для числа) 7 в истинное высказывание, а при подстановке цифры 2 — в ложное высказывание. Что касается так называемых связанных (или фиктивных) П., то они сами по себе вообще ничего не означают, несут чисто синтаксические функции и могут (при соблюдении некоторых элементарных предосторожностей) «переименовываться», то есть заменяться др. П. Такова, например, П. 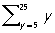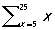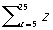у в записях или ∀yP (y), в интерпретации (прочтения) которых она вообще не входит и может быть заменена любой др. П. так, первая из них (читаемая как «сумма целых чисел от 5 до 25») может быть заменена на или , а вторая («все числа обладают свойством Р») на ∀tP (t). Различают индивидные, пропозициональные, предикатные, функциональные, числовые и др. виды П., вместо которых можно (согласно специальным правилам подстановки) подставлять соответственно обозначения предметов из рассматриваемой области («термы»), обозначения для конкретных высказываний, предикатов, функций, чисел и др. Т. о., П. можно содержательно понимать как «пустое место» в формуле, снабженное указанием, чем это «место» может быть «заполнено» (своего рода «тара под строго определенный товар»).

Свободные вхождения П. в выражения содержательных научных теорий и формулы логико-математических исчислений (соответствующие употреблению неопределенных местоимений в обычной речи) допускают различные интерпретации. Первая (соответствующая применению всякого рода процедур подстановок) — так называемая предикатная интерпретация: формула A (x₁. x_n) какого-либо исчисления понимается как некоторый местный Предикат. Та же формула может интерпретироваться и как предложение (Высказывание), а именно как предложение ∀x₁ … ∀x_n A (x₁ … x_n), являющееся ее «замыканием»,— это так называемая интерпретация всеобщности (употребительная, например, при формулировке аксиом (См. Аксиома) различных научных теорий). Свободным П. могут, наконец, приписываться значения, постоянные в пределах некоторого контекста (например, вывода из данной совокупности формул), их тогда называют параметрами этого контекста и говорят об их условной интерпретации. Например, П. х в выражении cos х, взятом изолированно, имеет предикатную интерпретацию, в тождестве sin 2 x + cos 2 x = 1 — интерпретацию всеобщности, в уравнении cos х = 1 (в процессе его решения, когда эта П. именуется «неизвестным») — условную интерпретацию.

Таким образом, на различных уровнях формализации понятие П. выступает как уточнение средств, общеупотребительных в обычных разговорных языках (неопределенные местоимения, неопределенные артикли), и различных способов использования этих средств.

Лит.: Клини С. К, Введение в метаматематику, пер с англ, М., 1957, §§ 31, 32, 45, Чёрч А, Введение в математическую логику, пер с англ, т. 1, М., 1960, §§ 02, 04, 06.

Источник